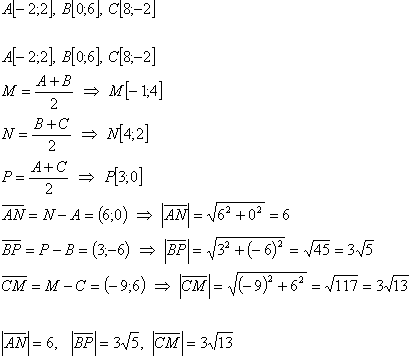Vector in a plane
1.Characterize the properties of a vector in a plane:
Solution:
2.Given are points A[-2;5], B[1;yB], and C[4;-3]. Determine B so that the following holds true:
a) vectors AB and AC are perpendicular
b) vectors AB and AC are parallel
Solution:
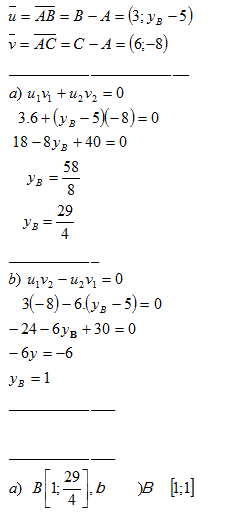
3.Given is vector v = AB as follows: A[1;1], B[b1;b2] and the center of the vector S[4;5].
Calculate the coordinates of point B and the magnitude of the vector.
Solution:
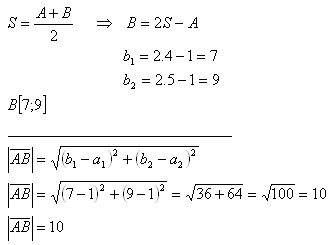
Point B has coordinates B[7;9]. The magnitude of the vector is 10 units.
4.The points A[2;-3] and B[x;0] are given.
Determine x so that the magnitude of the vector is |AB| = 5.
Solution:
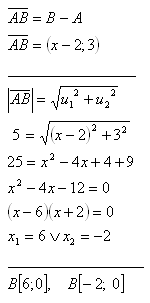
The coordinates of point B are: B[6;0] or B[-2;0].
5.Prove that the triangle whose vertices are points A[-3;-2], B[1;4], and C[-5;0] is isosceles.
Solution:
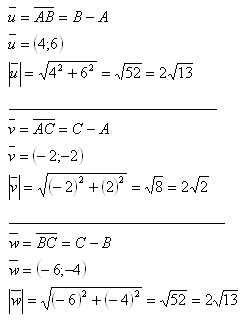
Since |u| = |w|, triangle ΔABC is isosceles.
6.Given are vectors a = (3;-2) and b = (-1;5).
Determine the vector c for which::
a.c = 17
b.c = 3
Solution:
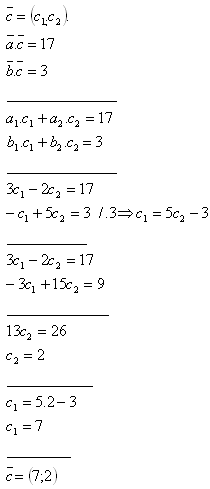
The vector sought is c = (7;2).
7.Find the vector v, perpendicular to the vector u = (3;4) and whose magnitude is 15.
Solution:
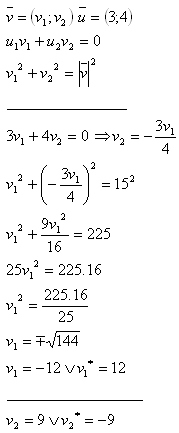The vector is v = (-12;9) or v = (12;-9).
8.The vertices of the triangle ΔABC are the points A[1;1], B[2;-1] and C[3;2].
Calculate the sizes of its interior angles.
Solution:
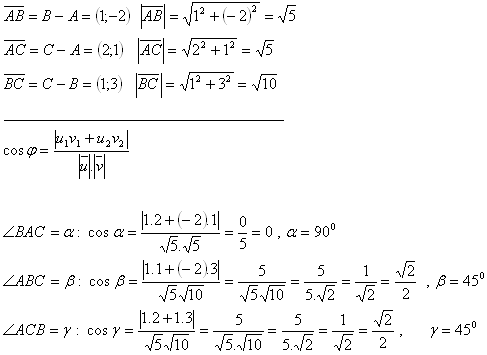The interior angles of the triangle are: α = 90°, β = 45° and γ = 45°.
9.On the coordinate axes, find the point that is 5 from point A [4;-6].
Solution:
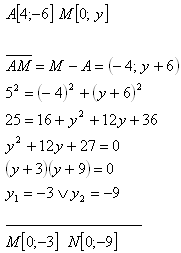On the y-axis, the points M[0;-3] and N[0;-9] are suitable. On the x-axis, there is no such point.
10.The vertices of the quadrilateral are at points: A[0;0], B[3;-4], C[6;0] and D[3;4].
Prove that the quadrilateral ABCD is a rhombus.
Solution:
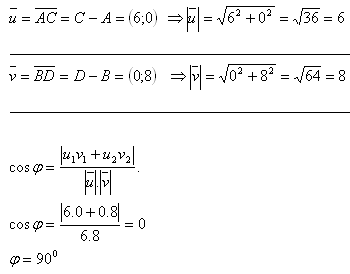Quadrilateral ABCD is a rhombus because it satisfies both conditions..
11.Points A, B, C are the vertices of triangle ABC. Show that triangle ABC is equilateral. Calculate its area.
Solution:
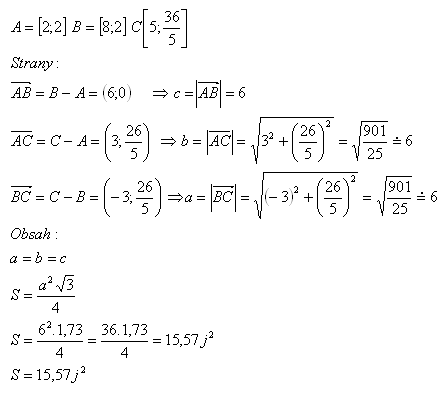
Triangle ABC is equilateral. Its area is S = 15.57j2.
12.Points A, B, C are the vertices of triangle ABC. Mark the midpoints of sides AC, BC as M,N. Show that the midpoint MN is parallel to side AB and that MN = 0.5AB.
Solve for A[2;2], B[10;4], C[4;8]]
Solution:
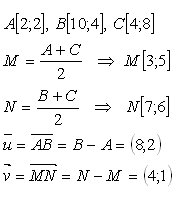
Parallelism condition:
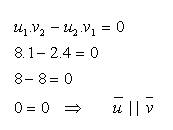
Property MN = 0.5.AB
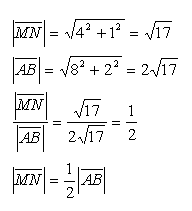
13.Given isosceles trapezoid ABCD with vertices
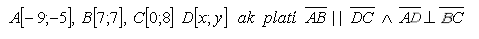
Determine the coordinates of point D.
Solution:
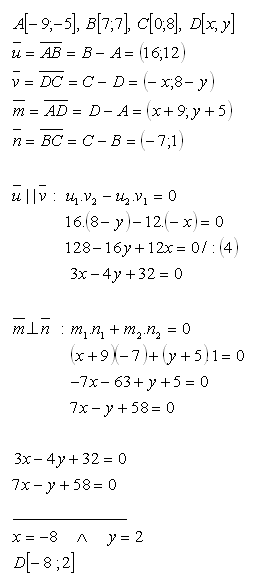
14.Determine the coordinates of the center S and the size of the radius r of the circle that passes through the points A,B,C. Solve for the points:
Solution:
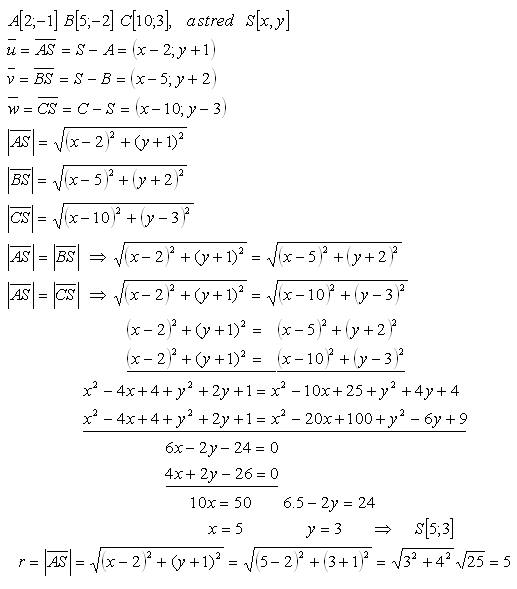
15.Find the coordinates of the center of gravity of a system of four bodies of equal mass, which lie at points A,B,C,D. The center of gravity T is the center of the line segment, whose endpoints are at the center of the vectors
Solution:
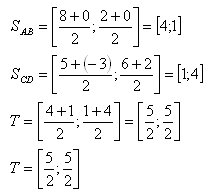
16.Point A [2;5] is the origin of the force F, whose projection on the coordinate axes is x = 3; y = 3. Calculate the end of the vector that represents the force F.
Also determine the magnitude of this force!
Solution:
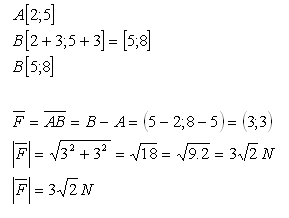
The end point of the force is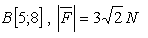 
17.Given are three points A,B,
- a.) Prove that they lie on the same line
- b.) Find the ratio of the magnitudes of the vectors
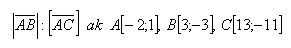
Solution:
a.) Parallelism condition:
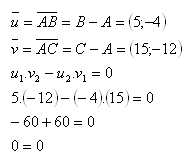
b.) Vector ratio:
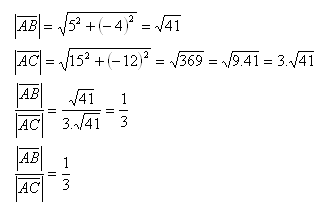
The vectors lie on a straight line and are in proportion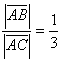 
18.An isosceles triangle ABC has base AB with vertex A and base center S. Its vertex C lies on the x-axis. Determine the vertices of the triangle B and C.
Solution:
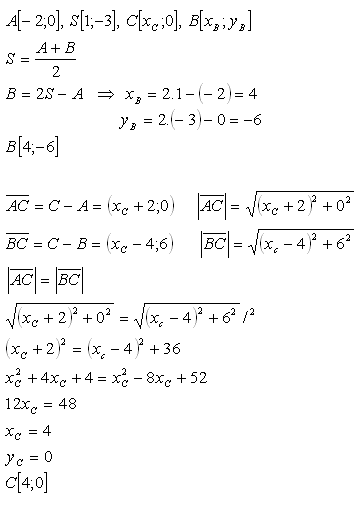
The desired vertices of triangle ABC are B[4;–6] and C[4;0].
19.Given a vector u = (5 ;-3) and a vector v = (1;yv) such that
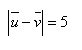
Determine yv
Solution:
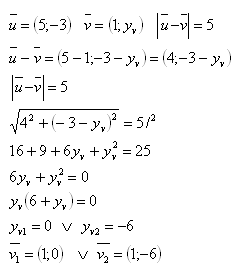
Vectors are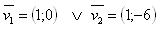 
20.Points A,B,C are the vertices of triangle ABC and points M,N,P are the midpoints of the sides of this triangle. Determine the coordinates of three vectors whose positions coincide with the medians of triangle ABC such that the starting point is always at the vertex of the triangle. Calculate the magnitudes of these vectors.
Solution:
