Kinetics
1. Na dovolenku idete autom po diaľnici 3 hodiny rýchlosťou 110 km.h-1.Potom na 30 minút zastavíte. Pokračujete dvojhodinovou jazdou stálou rýchlosťou 90 km.h-1 až do cieľa. Určite priemernú rýchlosť cestovania.
Riešenie:
Rozbor:
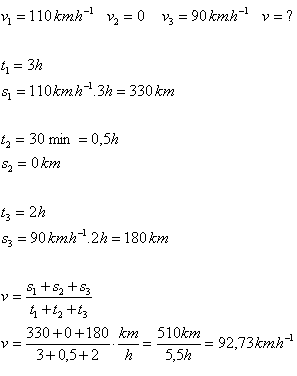
Priemerná rýchlosť cestovania bola v = 92,73 km.hod-1.
2.
Diaľničný úsek má dĺžku 25 km. Najväčšia povolená rýchlosť je 110 km.hod-1. Vodič tento úsek prešiel za 12 minút. Prekročil najväčšiu povolenú rýchlosť na diaľnici?
Riešenie:
Rozbor:
s=25 km = 2500 m; t=12 min = 720 sek.
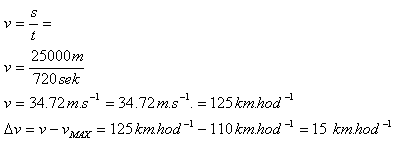
Vodič prekročil dovolenú rýchlosť o 15 km.hod-1
3.
Kolóna vojenských vozidiel má dĺžku 2 km . Pohybuje sa stálou rýchlosťou 30 km.hod-1. Vzdialenosť od čela kolóny ku poslednému vozidlu prešla spojka priemernou rýchlosťou 50 km.h-1. Naspäť rýchlosťou 60 km.h-1. Aký čas na to spojka na to potrebovala akú dráhu pri tom prešla?
Riešenie:
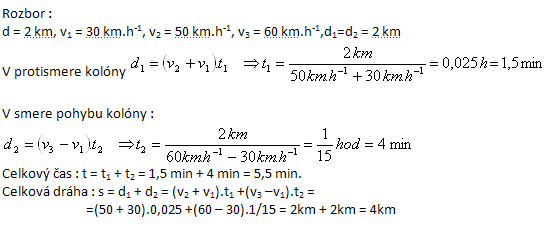
4. Voľne padajúce teleso má v bode A rýchlosť 3,0 m.s-1, v nižšie položenom bode B rýchlosť 7,0 m.s-1. Zistite za aký čas prejde vzdialenosť AB. Aká je vzdialenosť bodov A a B? Akou rýchlosťou teleso dopadne, ak jeho pohyb z bodu B na zem trvá ešte 2 s.
Riešenie:
Rozbor:
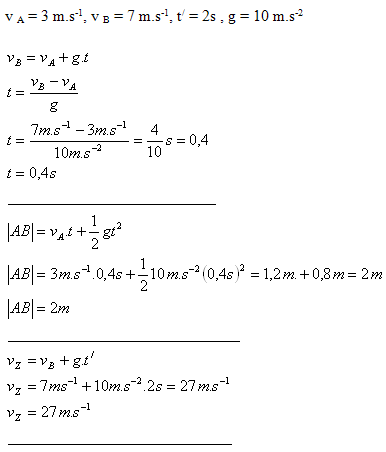
5.
Plavec, ktorého rýchlosť vzhľadom na vodu je 0,85 m.s-1 pláva v rieke, v ktorej voda tečie rýchlosťou 0,40 m.s-1. Určite čas, za ktorý dopláva z miesta A do B, vzdialeného 90 m, ak pláva:
- a) po prúde
- b) proti prúdu
- c) kolmo na prúd ( Výsledná rýchlosť je kolmá na rýchlosť prúdu).
Riešenie:
Rozbor:
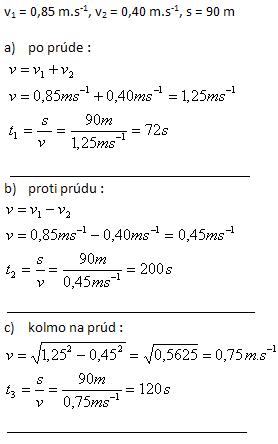
Plavec z A do B dopláva po prúde za t1 = 72s, proti prúdu za t2 = 200s a kolmo na prúd za t3 = 120s.
6. Motorová loďka plávajúca po rieke prešla vzdialenosť 120 m pri plavbe po prúde za 14s, pri plavbe proti prúdu za 24s. Určite rýchlosť loďky v1 vzhľadom na vodu s rýchlosť prúdu rieky v2.
Riešenie:
Rozbor:
v1 – rýchlosť loďky vzhľadom na vodu , v2 - rýchlosť prúdu rieky
t1 = 14s, t2 = 24s
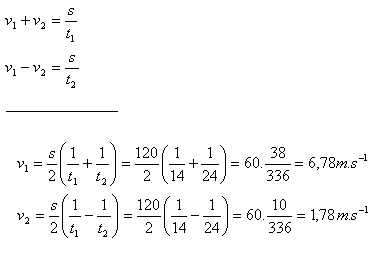
Rýchlosť loďky vzhľadom na vodu je 6,78 m.s-1, - rýchlosť prúdu rieky je 1,78m.s-1
7.
Automobilista prešiel prvú tretinu dráhy s stálou rýchlosťou v1, ďalšie dve tretiny rýchlosťou v2 = 72 km.h-1. Priemerná rýchlosť v bola 36 km.h-1. Vypočítajte v1!
Riešenie:
Rozbor:
v1 = ? , v2 = 72 km.h-1 = 20 ms-1, v = 36 km.h-1 = 10 m.s-1
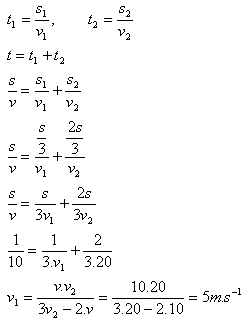
Prvú tretinu dráhy prešiel rýchlosťou v1 = 5 m.s-1
8.
Vodič osobného auta idúceho rýchlosťou 90 km.h-1 zbadal vo vzdialenosti 60 m pred sebou stojace nákladné auto. Zatlačil brzdy a dosiahol spomalenie a = 5 m.s-2. Aká bola brzdná dráha osobného auta? Narazilo do prekážky?
Riešenie:
Rozbor :
v = 90 km.h-1= 25 m.s-1, a = 5 m.s-2
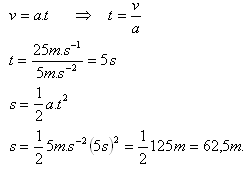
Brzdná dráha osobného auta bola s = 62,5 m. Auto narazilo do prekážky.
9.
Raketa dosiahne druhú kozmickú rýchlosť 11 km.s-1po prejdení dráhy 200 km. Za aký čas to dosiahne? Aké je jej zrýchlenie?
Riešenie:
Rozbor :
v = 11 km.s-1= 11 000 m.s-1, s = 200 km = 200 000 m.
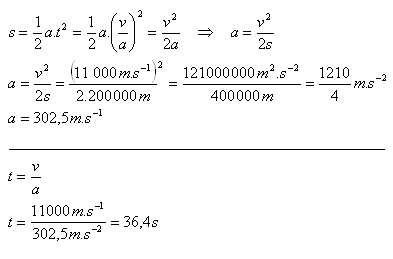
Raketa dosiahne druhú kozmickú rýchlosť za 36.4s. Jej zrýchlenie je 302,5 m.s-2.
10.
Vozík na koľajniciach vozíčkovej demonštračnej súpravy sa pohybuje so stálym zrýchlením a = 0,08 m.s-2 ( v0 = 0 , s0 = 0 )
- Vypočítajte dráhy, ktoré prešiel vozík v čase t = 1s, 2s, 3s, 4s, 5s.
- Zistite, aké dráhy prejde vozík v jednotlivých po sebe idúcich sekundách. V akom pomere sú tieto dráhy?
Riešenie:
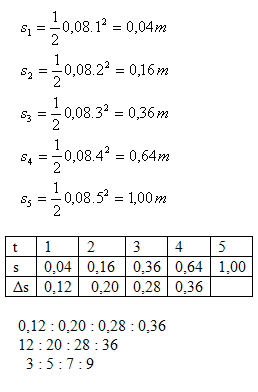
11.
Rušňovodič rýchlika, ktorý sa pohyboval rýchlosťou v1 = 108 km.h-1 zbadal vo vzdialenosti 180 m pred sebou nákladný vlak pohybujúci sa tým istým smerom rýchlosťou v2 = 32,4 km.h-1. Rušňovodič začal brzdiť a vlak spomalil so spomalením a = 1,2 m.s-2. Zistite, či sa vlaky zrazia.
Riešenie:
Rozbor :
s0 = 180 m, v1 = 108 km.h-1 = 30 m.s-1, v2 = 32,4 km.h-1 = 9 m.s-1, a = 1,2m.s-1
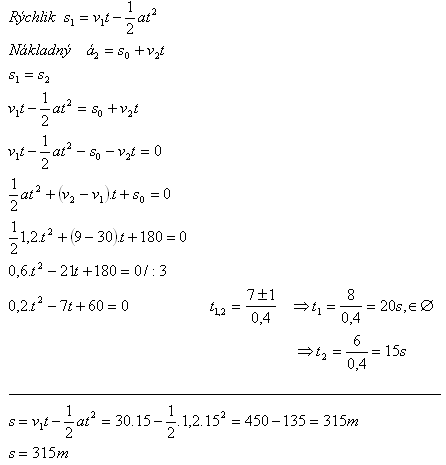
Vlaky sa zrazia v čase 15 s od začatia brzdenia vo vzdialenosti 315 m.
12.
Sekundová ručička hodiniek je o tretinu dlhšia ako minútová. V akom pomere sú rýchlosti ich koncových bodov?
Riešenie:
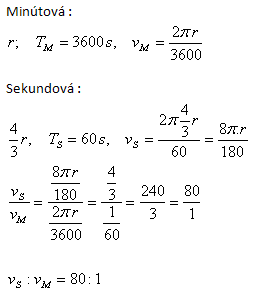
13.Zem obieha okolo Slnka približne rovnomerným pohybom po kružnici za 365,25 dňa. Aká je rýchlosť Zeme, ak vzdialenosť Zem – Slnko je približne 150 miliónov kilometrov.
Riešenie:
T = 365,25 dňa = 31557600 s =3,16.107s, r =150 000 000 km = 1,5.1011m.
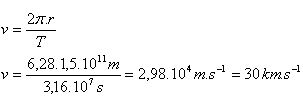
Zem obieha okolo Slnka obvodovou rýchlosťou 30 km.s-1
14.
Rýchlosť rovnomerného pohybu družice po kružnici okolo Zeme je 7,46 km.s-1. Družica sa pohybuje vo výške 800 km nad povrchom Zeme. (R = 6378 km) Určite obežnú dobu T družice okolo Zeme.
Riešenie:
R = 6378 km = 63,78.105m, h = 800 km = 8.105m, v = 7,46.103 m.s-1
r = R + h = 63,78.105m + 8.105m = 71,78.105m
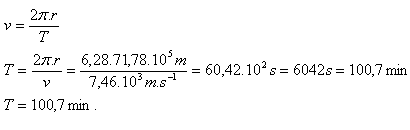
15.
Akú najmenšiu rýchlosť musí mať motocyklista, ak má jazdiť na vnútornom povrchu dutej gule s polomerom R = 6 m všetkými smermi? Ťažisko motocykla a jazdca je 0,9 m od povrchu.
Riešenie:
r = R – 0,9 = 6m - 0,9m = 5,1 m
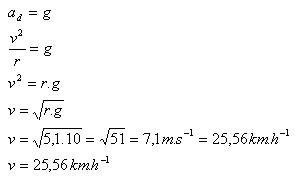
Najmenšia rýchlosť motocyklistu musí byť 25,56 km.h-1
16. Sedačka kolotoča je upevnená vo vzdialenosti 240 cm od stredu otáčania a vykonáva 18 otáčok za minútu. Určite jej obvodovú rýchlosť a dostredivé zrýchlenie.
Riešenie:
Rozbor :
r = 240 cm = 2,4 m, f = 18/60 s-1 = 0,3 s-1,
a)
v = 2π.r.f
v = 6,28.2,4m.0,3 s-1= 4,52 m.s-1
v = 4,52 m.s-1
b)
a d = 4π2.f2.r
a d = 4.9,8596.0,32.2,4 m.s-2= 8,52 m.s-2
a d = 8,52 m.s-2
Sedačka kolotoča má obvodovú rýchlosť 4,52 m.s-1
a dostredivé zrýchlenie 8,52 m.s-2.