sk|cz|de|

Physics

The surface of the liquid

1. Explain the physical concepts of “surface layer” and “capillarity”

Solution:

The surface and a drop of liquid, or a bubble, behave as if there were an elastic film on their surface – the “surface layer.” It has a thickness of about 10-9 m. It is formed by a layer of molecules. The surface and drop have one surface, a bubble has two surfaces.

Surface tension:

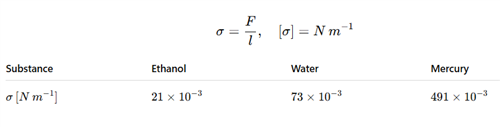
povrch-kvap-1-1 

Surface tension coefficients:

Substance σ [N m−1]\sigma \,[N \, m^{-1}]
Alcohol 21×10−321 \times 10^{-3}
Water 73.1×10−373.1 \times 10^{-3}
Mercury 491×10−3491 \times 10^{-3}

For: Surface, Droplet vs. Bubble, Membrane

Quantity   Surface, Droplet
   Bubble, Membrane
Surface force   F=σ⋅lF = \sigma \cdot l    F=2σ⋅lF = 2\sigma \cdot l
Surface energy   E=σ⋅SE = \sigma \cdot S    E=2σ⋅SE = 2\sigma \cdot S
Capillary pressure   p=2σRp = \tfrac{2\sigma}{R}    p=4σRp = \tfrac{4\sigma}{R}
Hydrostatic pressure   p=ρghp = \rho g h    p=ρghp = \rho g h

  l = 2π.r      S = π.r2

  • Capillary elevation = rise of a wetting liquid in a capillary
  • Capillary depression = lowering of a non-wetting liquid in a capillary

2.What is the mass of a water drop (σ = 73.10-3 N.m-1) that dripped from a tube with a radius of 0.5 mm?

Solution:

Analysis:

R = 0.5·10-3 m,  g = 10 m.s-2,  σ = 73.10-3 N.m-1

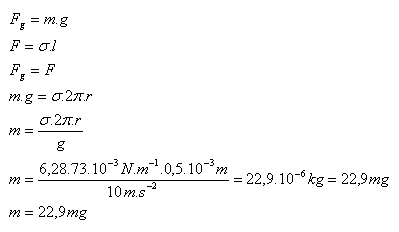
fyzika-povrch-kvapalin-2.gif 

The mass of the water drop is m = 22.9 mg.

3.A capillary measured 100 drops of ethanol with a mass of 1.81 g. The same number of water drops from the same capillary and at the same temperature has a mass of 6.26 g. Determine the surface tension of ethanol σ1 if the surface tension of water is σ2(H2O) = 73.10-3 N.m-1.

Solution:

Analysis:

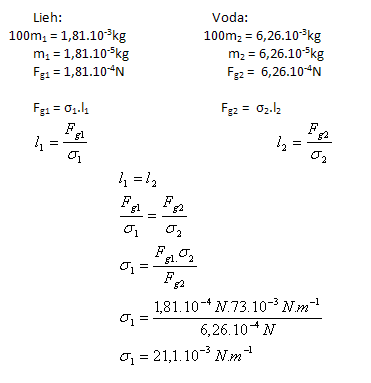
 fyzika-povrch-kvapalin-3.gif

The surface tension of ethanol is σ1 = 21.1·10-3 N.m-1

4.Water drips from a capillary with radius r = 0.9 mm. How many drops of water are in 1 cm3 of water? (σ = 73.10-3 N.m-1, ρ = 103 kg.m-3)

Solution:

r = 0.9 mm = 0.9·10-3 m,  V0 = 1 cm3 = 10-6 m3, σ = 73.10-3 N.m-1,  ρ = 103 kg.m-3

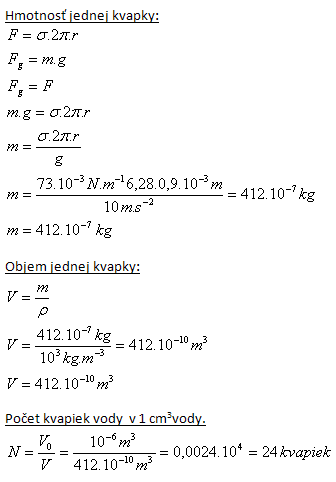
fyzika-povrch-kvapalin-4.gif 

There are 24 drops in 1 cm3 of water.

5.A movable rod with a length of 40 mm on a frame with a soap film is in equilibrium when loaded with a weight of 320 milligrams. What is the surface tension of the soap solution in water in contact with air? The film has two surfaces. (Neglect the mass of the rod)

Solution:

Analysis:

l = 40·10-3 m = 0.04 m,  m = 320·10-6 kg,  σ = ?

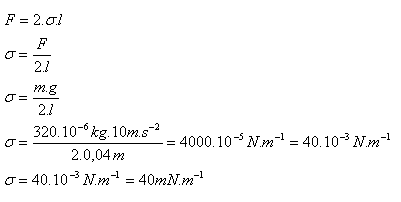
 fyzika-povrch-kvapalin-5.gif

The surface tension of the soap solution in water is σ = 40 mN.m-1.

6. Determine the work (in an isothermal process) required to inflate a soap bubble with a diameter of 14 cm. The bubble has two surfaces. σ = 40·10-3 N.m-1

Solution:

Analysis:

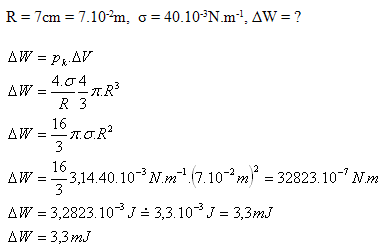
fyzika-povrch-kvapalin-6.gif 

The work required to inflate the soap bubble is W = 3.3 mJ.

7.A soap bubble (σ = 40·10-3 N.m-1) has a radius of 2 cm. What work is done if we increase its radius by 1 cm?

Solution:

Analysis:

R1 = 2·10-2 m,  R2 = 3·10-2 m,  σ = 40·10-3 N.m-1,   ΔW = ?

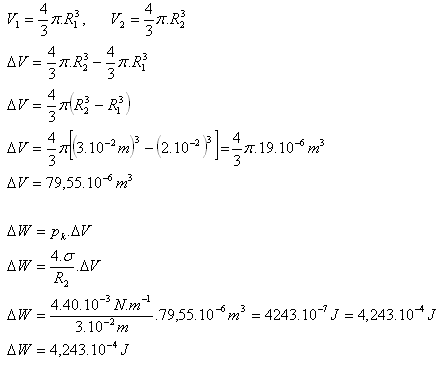
 fyzika-povrch-kvapalin-7.gif

If we increase the bubble radius by 1 cm, the work done is 4.243·10-4 J.

8. Capillary rise – elevation – of ethanol in a narrow capillary is 12 mm. What is the inner diameter of the capillary? (ρ = 800 kg.m-3, σ = 21.4 mN.m-1)

Solution:

Analysis:

h = 12·10-3 m,  ρ = 800 kg.m-3, σ = 21.4·10-3 N.m-1

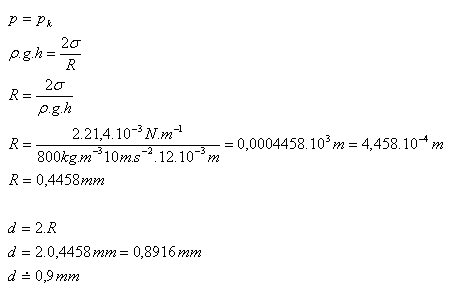
 fyzika-povrch-kvapalin-8.gif

The inner diameter of the capillary is about d = 0.9 mm.

9.The capillary has an inner diameter of 0.2 mm. Calculate:

  • a.) How high will benzene rise in the capillary (ρ = 870 kg.m-3, σ = 29,1.10-3N.m-1)
  • b.) How does the rise height of benzene change if we use a capillary with double the radius
  • c.) How would the result of the experiment change on the Moon. (gM = 0.167g)

Solution:

Analysis:

R = 0.1mm =  10-4m,  ρ = 870 kg.m-3,  σ = 29,1.10-3N.m-1, gM = 0.167gZ

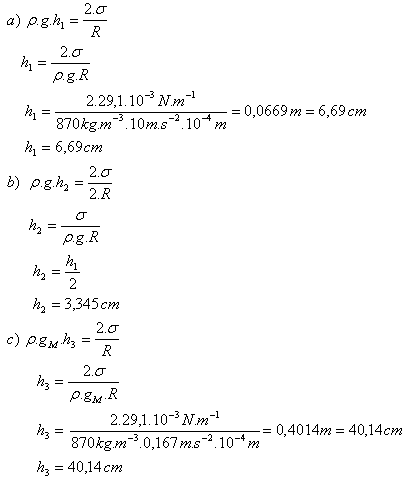
 fyzika-povrch-kvapalin-9.gif

10. What will be the difference in levels in two capillaries immersed in a liquid (ρ = 800 kg.m-3, σ = 22.10-3N.m-1)? The capillaries have different inner diameters: d1 = 0.4mm, d2 = 1mm

Solution:

Analysis:

R1 = 0.2.10-3m,  R2 = 0.5.10-3m,  ρ = 800 kg.m-3,  σ = 22.10-3N.m-1

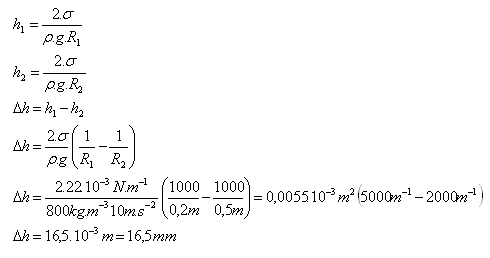
 fyzika-povrch-kvapalin-10.gif

The difference in levels in the capillaries will be 16,5 mm.

11.On a frame with a movable partition of length 10 cm there is a soap film. What work must be done to move the partition by 2 cm?

Solution:

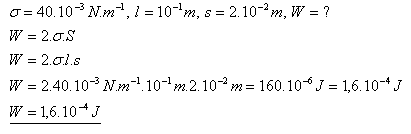
povrch-kvapalin-11 

When the partition is moved, work of 1.6.10–4J must be done.

12.A small frame with a movable arm of mass 1.2 g is in a vertical position. The weight force keeps the arm and the film in equilibrium. What is the length of the arm if the surface tension of the film is 60.10-3N.m-1? How does the surface energy of the film change if the arm is moved by 2 cm?

Solution:

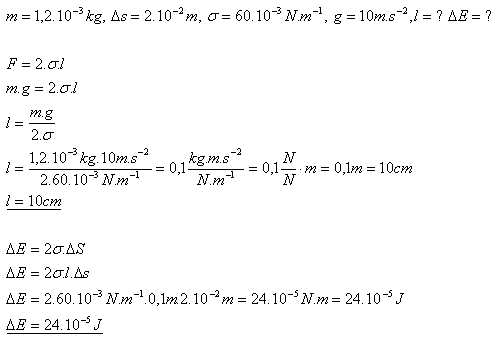
povrch-kvapalin-12

The length of the arm is 10 cm. The surface energy of the film increases by 24.10-5J

13.A water droplet with a radius of 3 mm is sprayed into tiny droplets with a radius of 3.10-5 mm. By how many times does the surface energy of the water droplets increase in the process?

Solution:

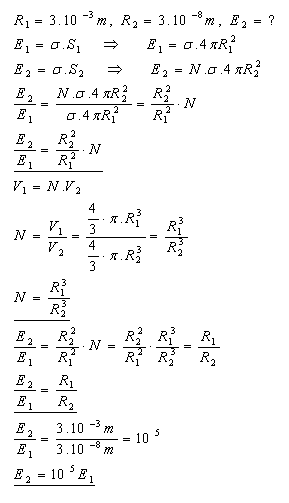
povrch-kvapalin-13

14.What is the pressure of the air in a soap bubble with a radius of 2 mm if the atmospheric pressure is 101325 Pa?

Solution:

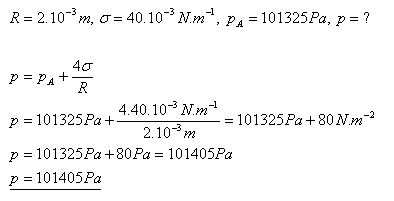
povrch-kvapalin-14

The pressure of the air in the soap bubble is 101405 Pa.

15.In a capillary, kerosene rose to a height of 13 mm and in another capillary with the same radius mercury fell by 13.9 mm. What is the surface tension of mercury, if the density of mercury is 13.6.103 kg.m3? The surface tension of kerosene is 27.10-3N.m-1 and its density is 0.8.103 kg.m-3.

Solution:

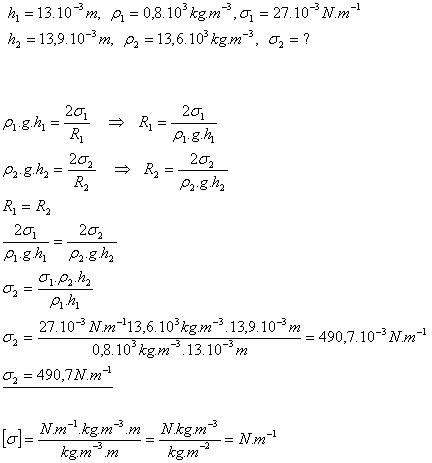
povrch-kvapalin-15

The surface tension of mercury is 491 N.m-1.

16. In a capillary with a diameter of 2 mm there is water. How tall a column of water will remain in the capillary if both ends remain open?

povrch-kvapalin-16z.gif

Solution:

The water column will be held by two menisci, the upper and the lower. Each acts on the water with a surface force F, which is in equilibrium with the weight of the water.

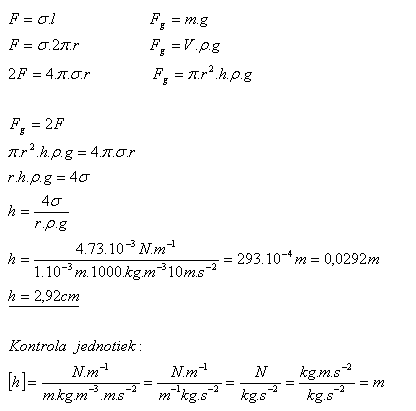
povrch-kvapalin-16r

The water column in the capillary will be 2.92 cm high.

17.From a capillary, 100 drops of water with a total mass of 2.4 g dripped. The mass of 50 drops of glycerine from the same capillary is 1.1 g. What is the ratio of the surface tensions of the two liquids?

Solution:

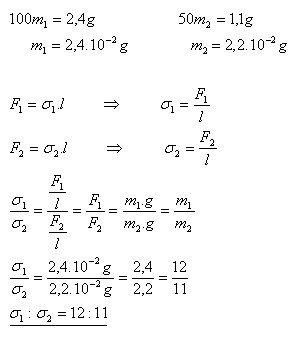
povrch-kvapalin-17

The ratio of the surface tensions of the two liquids is 12:11

18. What is the surface tension of glycerine? (Use the result of problem 17)

Solution:

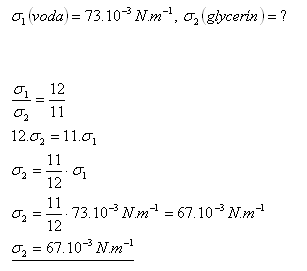
povrch-kvapalin-18

The surface tension of glycerine is 67.10–3N.m-1

19.When N water droplets with a radius of 2.10–6 m merge into one droplet with a radius of 2.10–3 m, 3.668 mJ of energy is released. By how much does the water heat up?

Solution:

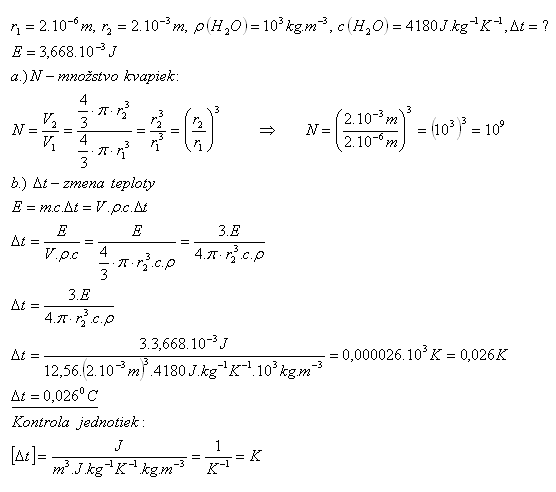
povrch-kvapalin-19

The water warms up by 0.0260C.

20.Calculate the surface energy of a mercury droplet that has a volume of 1 cm3.

Solution:

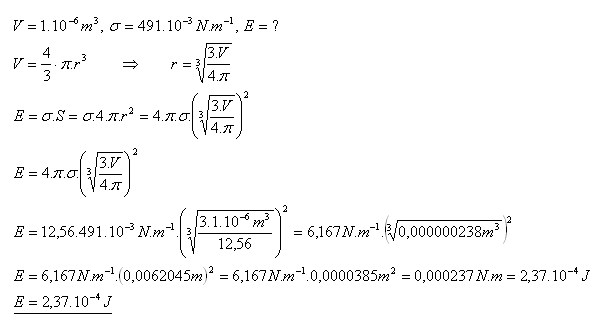
povrch-kvapalin-20

The surface energy of the mercury droplet is 2.37.10–4J.