Povrch kvapalín
1. Vysvetlite fyzikálne pojmy „povrchová vrstva“ a „kapilarita“
Riešenie:
Hladina a kvapka kvapaliny, bublina sa správajú tak, ako by na ich povrchu bola pružná blanka - „povrchová vrstva“. Má hrúbku asi 10-9m. Je tvorená vrstvou molekúl. Hladina a kvapka majú jeden povrch, bublina dva povrchy.
Povrchové napätie:
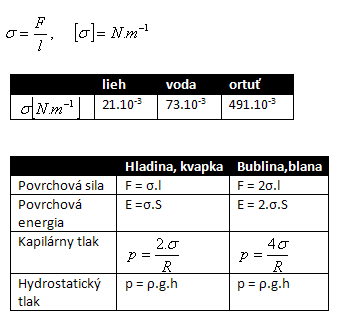
l = 2π.r S = π.r2
- Kapilárna elevácia = zvýšenie hladiny zmáčavej kvapaliny v kapiláre
- Kapilárna depresia = zníženie hladiny nezmáčavej kvapaliny v kapiláre
2.Aká je hmotnosť kvapky vody (σ = 73.10-3N.m-1), ktorá odkvapla z rúrky s polomerom 0,5 mm?
Riešenie:
Rozbor:
R = 0,5.10-3m, g = 10 m.s-2, σ = 73.10-3N.m-1
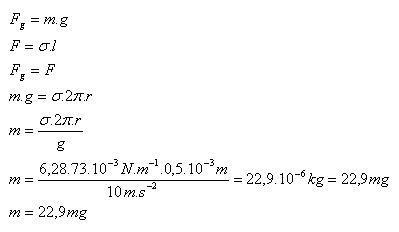
Hmotnosť kvapky vody je m = 22,9 mg.
3.Kapilára odmerala 100 kvapiek liehu s hmotnosťou 1,81g. Rovnaký počet kvapiek vody z tej istej kapiláry a tej istej teploty má hmotnosť 6,26g. Určite povrchové napätie liehu σ1(lieh) ak viete, že povrchové napätie vody je σ2(H2O) = 73.10-3N.m-1.
Riešenie:
Rozbor:
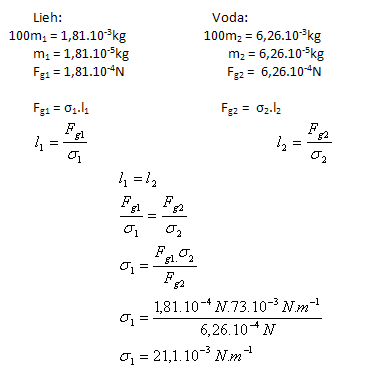
Povrchové napätie liehu je σ1 = 21,1,10-3 N.m-1
4.Voda odkvapkáva z kapiláry s polomerom r = 0,9 mm. Koľko kvapiek vody je v 1 cm3 vody? (σ = 73.10-3N.m-1, ρ = 103kg.m-3)
Riešenie:
r = 0,9 mm = 0,9.10-3m, V0 = 1cm3 = 10-6m3, σ = 73.10-3N.m-1, ρ = 103kg.m-3
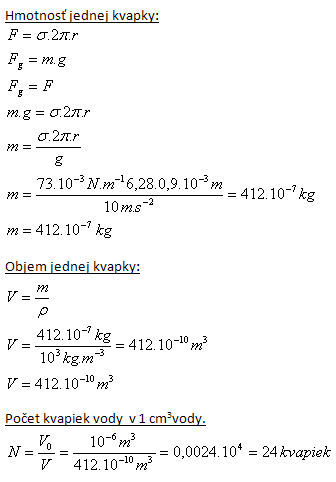
V 1cm3 vody je 24 kvapiek.
5.Pohyblivá priečka s dĺžkou 40mm na rámčeku s mydlovou blanou je v rovnováhe, ak je zaťažená závažím o hmotnosti 320 miligramov. Aké je povrchové napätie mydlového roztoku vo vode v styku so vzduchom? Blana má dva povrchy. (Hmotnosť priečky zanedbať)
Riešenie:
Rozbor:
l = 40.10-3m = 0,04m, m = 320.10-6kg, σ = ?
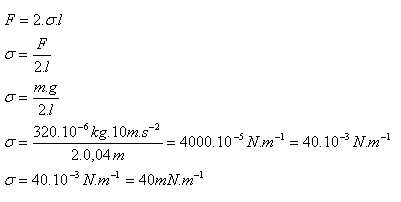
Povrchové napätie mydlového roztoku vo vode je σ = 40 mN.m-1.
6. Určite prácu (pri izotermickom deji), ktorú treba vykonať pri nafúknutí mydlovej bubliny s priemerom 14 cm. Bublina má dva povrchy. σ = 40.10-3N.m-1
Riešenie:
Rozbor:
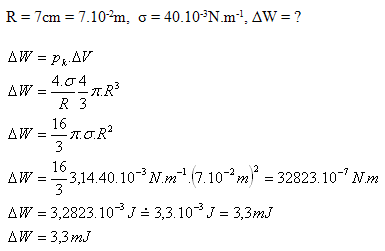
Pri nafúknutí mydlovej bubliny treba vykonať prácu W = 3,3 mJ.
7.Mydlová bublina (σ = 40.10-3N.m-1) má polomer 2cm. Akú prácu vykonáme, ak zväčšíme jej polomer o 1cm?
Riešenie:
Rozbor:
R1 = 2.10-2m, R2 = 3.10-2m, σ = 40.10-3N.m-1, ΔW = ?
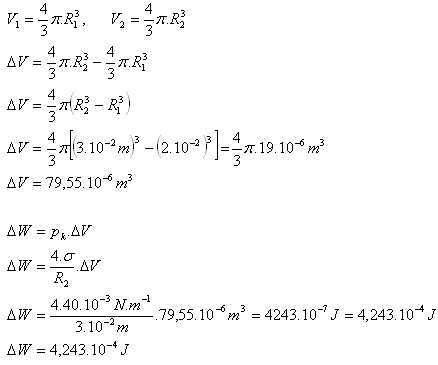
Ak zväčšíme jej polomer bubliny o 1cm vykonáme prácu 4,243.10-4J.
8. Kapilárne zvýšenie – elevácia – liehu je v úzkej kapiláre 12mm. Aký je vnútorný priemer kapiláry? (ρ = 800 kg.m-3, σ = 21,4 mN.m-1)
Riešenie:
Rozbor:
h = 12.10-3m, ρ = 800 kg.m-3, σ = 21,4.10-3N.m-1
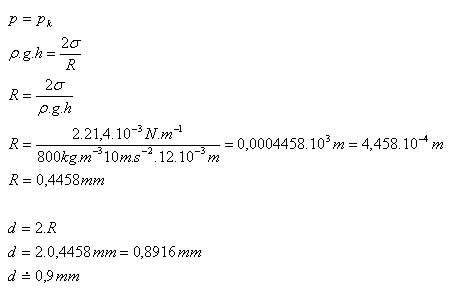
Vnútorný priemer kapiláry je asi d = 0,9 mm.
9.Kapilára má vnútorný priemer 0,2 mm. Vypočítajte:
- a.) Ako vysoko vystúpi v kapiláre benzén (ρ = 870 kg.m-3, σ = 29,1.10-3N.m-1)
- b.) Ako sa zmení výška výstupu benzénu, ak použijeme kapiláru s dvojnásobným polomerom
- c.) Ako by sa zmenil výsledok pokusu na Mesiaci.(gM = 0,167g)
Riešenie:
Rozbor:
R = 0,1mm = 10-4m, ρ = 870 kg.m-3, σ = 29,1.10-3N.m-1, gM = 0,167gZ
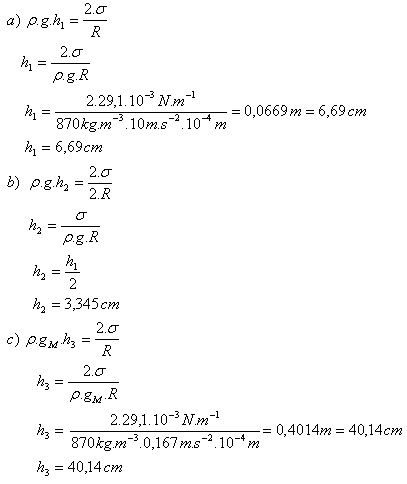
10. Aký bude rozdiel hladín v dvoch kapilárach ponorených do kvapaliny (ρ = 800 kg.m-3, σ = 22.10-3N.m-1). Kapiláry majú rozdielne priemery vnútorného povrchu: d1 = 0,4mm, d2 = 1mm
Riešenie:
Rozbor:
R1 = 0,2.10-3m, R2 = 0,5.10-3m, ρ = 800 kg.m-3, σ = 22.10-3N.m-1
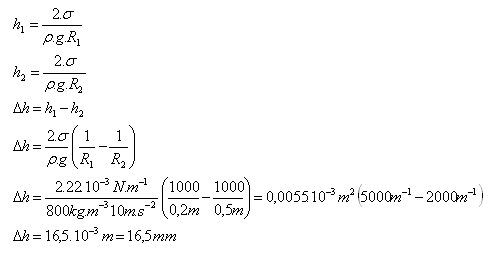
Rozdiel hladín v kapilárach bude 16,5 mm.
11.Na ráme s pohyblivou priečkou s dĺžkou 10 cm je mydlová bublina. Akú prácu treba vykonať, aby sa priečka posunula o 2cm.
Riešenie:
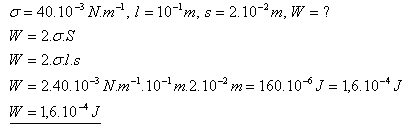
Pri posunutí priečky treba vykonať prácu 1,6.10–4J.
12.Rámček s pohyblivým ramenom s hmotnosťou 1,2g je v zvislej polohe. Tiažová sila dlží rameno a blanu v rovnováhe. Aká je dĺžka ramena , ak povrchové napätie blany je 60.10-3N.m-1. Ako sa zmení povrchová energia blany, ak sa rameno posunie o 2cm.
Riešenie:
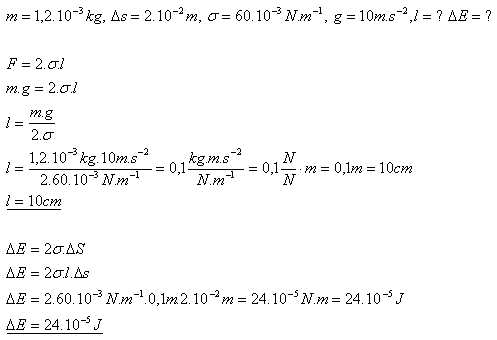
Dĺžka ramena je 10cm. Povrchová energia blany sa zväčší o 24.10-5J
13.Vodnú kvapku s polomerom 3mm rozprášime na drobné kvapôčky s polomerom 3.10-5mm. Koľkokrát sa pri tom zväčší povrchová energia vodných kvapiek?
Riešenie:
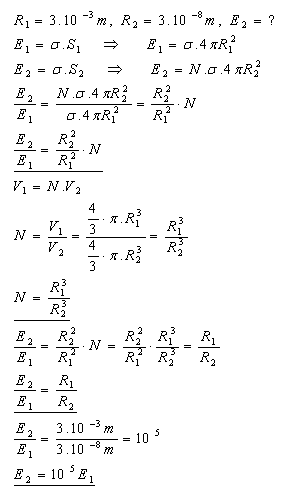
14.Aký tlak má vzduch v mydlovej bubline s polomerom 2 mm, ak atmosférický tlak je 101325 Pa?
Riešenie:
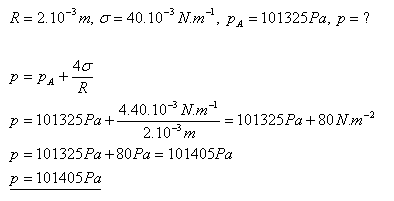
Tlak vzduchu v mydlovej bubline je 101405 Pa.
15.V kapiláre vystúpil petrolej do výšky 13mm a v inej kapiláre s rovnakým polomerom poklesla ortuť o 13,9mm. Aké je povrchové napätie ortuti, ak hustota ortuti je 13,6.103kg.m3. Povrchové napätie petroleja je 27.10-3N.m-1 a jeho hustota je 0,8.103kg.m-3.
Riešenie:
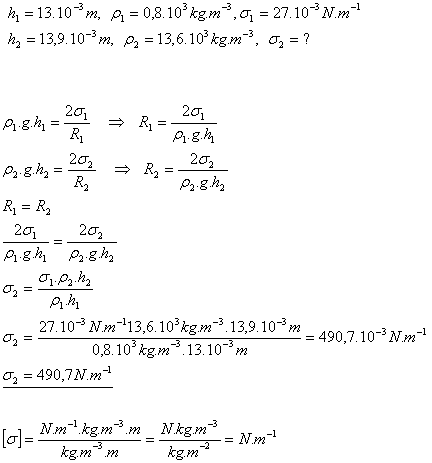
Povrchové napätie ortuti je 491 N.m-1.
16. V kapiláre s priemerom 2 mm je voda. Aký vysoký stĺpec vody zostane v kapiláre, ak obidva jej konce zostanú otvorené.
Riešenie:
Stĺpec vody budú udržiavať dva menisky, vrchný a spodný. Každý pôsobí na vodu povrchovou silou F, ktorá je v rovnováhe s tiažovou silou vody.
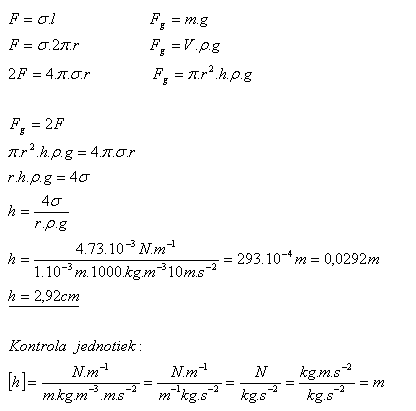
Stĺpec vody v kapiláre bude 2,92 cm vysoký.
17.Z kapiláry odkvapkali 100 kvapiek vody celkovej hmotnosti 2,4g. Hmotnosť 50 kvapiek glycerínu z tej istej kapiláry je 1,1g. Aký je pomer povrchových napätí obidvoch kvapalín?
Riešenie:
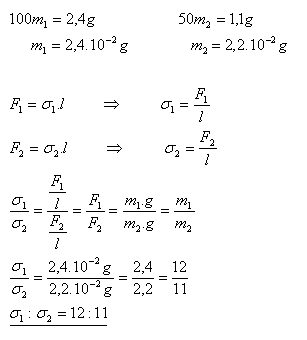
Pomer povrchových napätí obidvoch kvapalín je 12:11
18. Aké je povrchové napätie glycerínu? (Použite výsledok príkladu 17)
Riešenie:
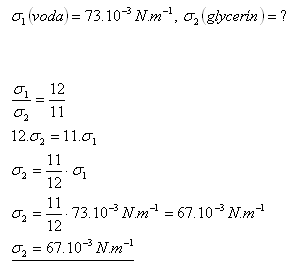
Povrchové napätie glycerínu je 67.10–3N.m-1
19.Pri spojení N vodných kvapiek s polomerom 2.10–6m do jednej kvapky s polomerom 2.10–3m sa uvoľní 3,668 mJ energie. O koľko sa voda ohreje?
Riešenie:
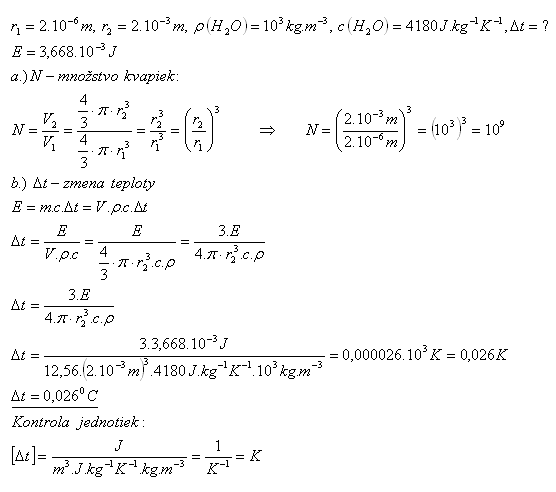
Voda sa ohreje o 0,0260C.
20.Vypočítajte povrchovú energiu kvapky ortuti, ktorá má objem 1cm3.
Riešenie:
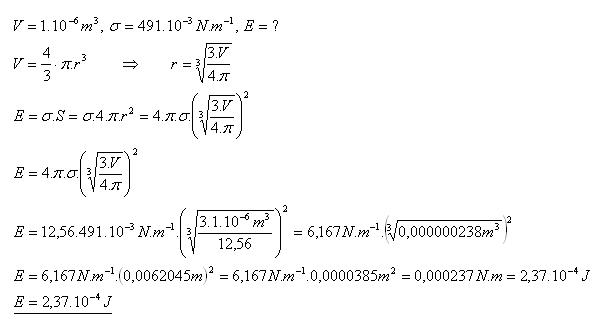
Povrchovú energia kvapky ortuti je 2,37.10–4J.