Ludolfovo číslo v starom Grécku
V pokračovaní nášho predchádzajúceho príspevku sa pozrieme, ako sa jednotlivé národy staroveku vyrovnali s hodnotou pre Ludolfovo číslo π.
Starogrécka matematika.
Tháles z Milétu, Demokritos z Abdéry, Pythagoras zo Samu, Euklides boli zvučné mená geniálnych filozofov a matematikov tohto obdobia. Hlavne dielo Euklida „Základy“ bolo považované za „najučenejšie dielo hneď po Biblii“. Archimedes zo Syrakúz (asi 287 – 212 pred n.l.) v diele „Meranie kruhu“ predpokladá, že „pomer obsahu kruhu a štvorca jeho priemeru je približne rovný 11:14“.
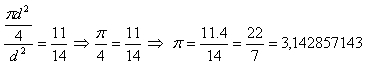
Claudius Ptolemajos (85 – 165 n. l.), známy svojou geocentrickou sústavou vesmíru, vydal okolo roku 140 dielo „Veľká zbierka“ známe pod arabským názvom „Almagest“. V ňom autor uvádza :
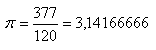
Odbočme teraz od starogréckych matematikov a položme si otázku: „Môže nesprávny matematický postup viesť k približne správnemu výsledku?“ Môže !!! Holandský matematik Valentín Otho (1550 – 1603) iste poznal Archimedovu aj Ptolemajovu hodnotu čísla π. Netradičným, nesprávnym odčítaním týchto hodnôt dostal:
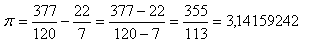
Dosiahol presnosť na šesť desatinných miest.
Rímska matematika.
Rímsky prínos k matematike je skoro nulový. V.P. Marcus (50 pred n. l.- 15 n. l.) v svojom diele „Desať kníh o architektúre“ tvrdí: „U kolesa, ktorého priemer je štyri a jedna šestina stopy, obvod činí dvanásť a jedna polovica stopy“.
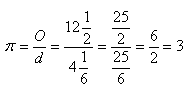
V tomto diele môžeme pozorovať, ako matematické vedomosti v Európe začali stále viac upadať. Ťažisko matematického bádania sa začalo presúvať do Číny, Indie a do Strednej a Malej Ázie.