Extrémy – slovné úlohy
1.Číslo 32 rozložte na dvoch sčítancov tak, aby ich súčin bol najväčší.
Riešenie:
Prvý sčítanec : x x = 16
Druhý sčítanec : 32 – x 32 – 16=16
y = x.(32 – x)
y = 32x – x2
y‘ = 32 – 2x
32 – 2x = 0
2x = 32
x =16
y‘‘ = -2 < 0 - maximum
Prvý sčítanec je 16, druhý tiež 16
2.Číslo 16 rozložte na dvoch sčítancov tak, aby súčet druhých mocnín týchto sčítancov bol najmenší.
Riešenie:
Prvý sčítanec : x x = 8
Druhý sčítanec : 16 – x 16 – 8 = 8
y = x2 + ( 16 – x )2
y = x2 + 256 -32x +x2
y = 2x2 – 32x + 256
y‘ = 4x – 32
4x - 32 = 0
4x = 32
x = 8
y‘‘ = 4 > 0 - minimum
Prvý sčítanec je 8, druhý tiež 8.
3.Nájdite také kladné číslo x, aby súčet tohto čísla a jeho prevrátenej hodnoty bol najmenší.
Riešenie:
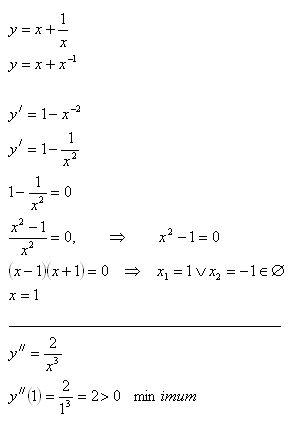
Hľadané číslo je x = 1.
4.Z drôtu dĺžky l = 120 cm máme urobiť model kvádra so štvorcovou podstavou. Aké má mať rozmery, aby povrch bol maximálny?
Riešenie:
Hrana štvorcovej podstavy : a = b =x
Výška kvádra : c
8x + 4c = l
8x +4c =120/:4
2x + c = 30
c = 30 – 2x
S = 2( ab + ac + bc )
S = 2( x.x + x(30 – 2x) + x(30 – 2x))
S = 2(-3x2 +60x )
S = -6x2 +120x
S‘ = -12x + 120 S‘‘ = -12 < 0 maximum
-12x + 120 = 0
12x = 120
x = 10
c = 30 -2x = 30 – 2.10 = 10
x = 10 cm, c = 10 cm .
Kváder musí mať tvar kocky s hranou x = 10 cm
5. Záhrada tvaru obdĺžnika má obvod 200 m. Určite rozmery záhrady tak, aby jej obsah bol maximálny.
Riešenie:
a = x
O = 2a + 2b
200 = 2x +2b/:2
100 = x + b
b = 100 – x b = 100 – x = 100 – 50 = 50
b = 50 m
S = a.b
S = x.(100 – x )
S = 100x – x2
S‘ =100 – 2x S‘‘ = -2 < 0 - maximum
100 – 2x = 0
2x = 100
x = 50
a = 50 m
Záhrada bude mať maximálny obsah ak bude tvaru štvorca o strane a = b = 50 m.
6.Kedy má kváder s objemom V = 63 cm3 a výškou v = 7 cm najmenší povrch?
Riešenie:
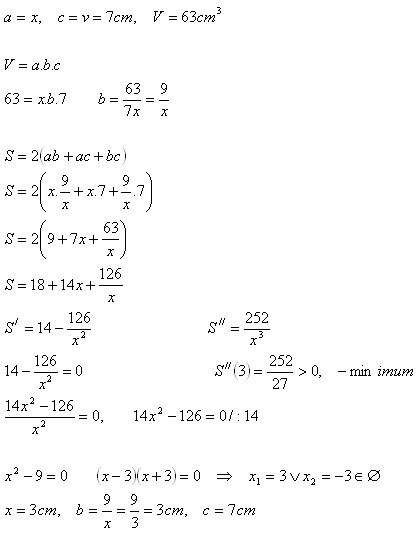
Rozmery hľadaného kvádra sú a = 3 cm, b = 3 cm, c = 7 cm
7.Na brehu rieky treba oplotiť záhradu obdĺžnikového tvaru (jednu stranu obdĺžnika tvorí rieka) pletivom dlhým l = 800 m. Aké rozmery musí mať záhrada , aby jej výmera bola maximálna ?
Riešenie:
800 = 2a +b
a = x
b = 800 – 2a = 800 – 2x
S = a.b
S = x.(800 – 2x)
S = 800x – 2x2
S‘ =800 – 4x S‘‘ = -4 < 0 - maximum
800 – 4x = 0
4x = 800
x = 200
x = 200 m
b = 800 – 2x
b = 800 – 400 = 400
b = 400 m
Rozmery záhrady sú a = 200 m, b = 400 m.
8.Aké sú rozmery otvoreného bazéna so štvorcovým dnom, ak bazén má objem V = 32 m3 a ak na jeho vymurovanie sa má spotrebovať minimálne množstvo materiálu.
Riešenie:
V = 32 m3, x – hrana štvorcovej podstavy, v – výška kvádra
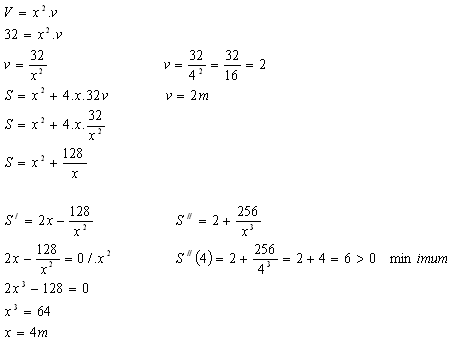
Rozmery: a=4m, b=4m, v=2m
9. Drôt s dĺžkou 5 m ohnite do pravého uhla tak, aby vzdialenosť obidvoch koncov bola minimálna. Kde treba drôt ohnúť?
Riešenie:
Odvesny a = x, b = 5 – x
Prepona c = y
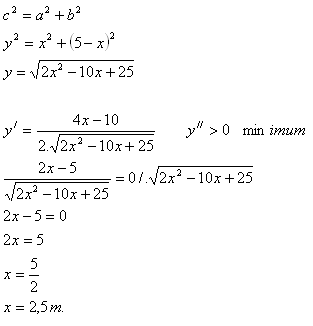
Drôt treba ohnúť v prostriedku.
10. Z plechu tvaru štvorca so stranou 30 cm treba v rohoch vystrihnúť štyri rovnaké štvorčeky , zvyšok prehnúť tak, aby vznikla otvorená škatuľa. Určite stranu odstrihnutých štvorčekov x tak, aby objem škatule bol maxi-málny.
Riešenie:
a = 30 – 2x, b = 30 – 2x, c = x
V = a.b.c
V = (30 – 2x)(30 – 2x).x
V = 4x3 – 120x2 +900x
V‘ = 12x2 – 240x +900 V‘‘ = 24x -240
12x2 – 240x +900 =0 /:12 V‘‘(5) = 24.5-240 = -120 < 0 maximum
x2 - 20x + 75 = 0
( x – 5 )( x -15 ) = 0 x1 = 5 x2 = 15 -nevyhovuje
x = 5 cm
Strana odstrihnutého štvorčeka je x = 5 cm.
11.Jama s objemom 500 m3 má tvar kvádra so štvorcovou podstavou so stranou x a hĺbkou h. Pri akých rozmeroch x a h bude mať jama minimálny povrch?
Riešenie:
Rozbor:
V = 500 m3, x = ?, h = ?
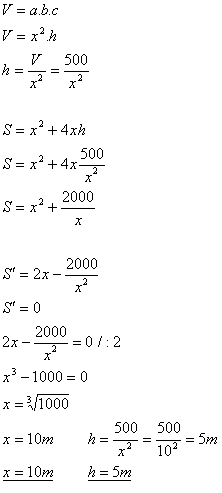
Jama má podstavu štvorec o strane x = 10m a výšku h = 5m.
12.Daná je parabola y = 4 – x2. Nájdite vrcholy obdĺžnika ABCD s najväčším obvodom, ktorého vrcholy A,B ležia na osi x , vrcholy C,D majú kladné y-ové súradnice a ležia na parabole.
Riešenie:
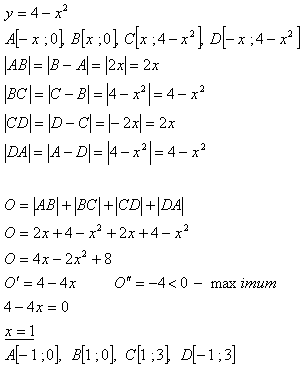
Body sú: A[-1;0], B[1;0], C[1;3], D[-1;3]
13.Určite rozmery (r, v) valcovej nádoby bez veka, ktorej povrch je S = 27π tak, aby jej objem bol najväčší.
Riešenie:
Rozbor:
S = 27π, r = x
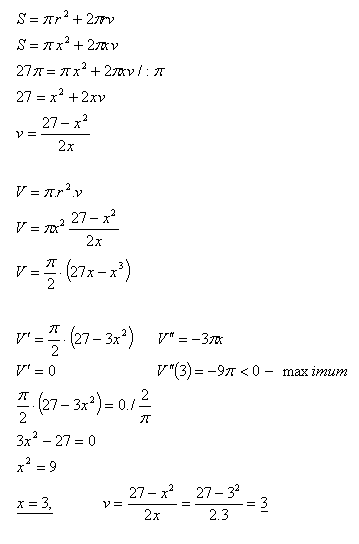
Rozmery nádoby sú r = x = 3j, v = 3j.
14.Hore otvorená nádoba tvaru valca má objem V = 3140 cm3. Určite rozmery valca (r, v) tak, aby na vytvorenie tejto nádoby sa minulo najmenej materiálu.
Riešenie:
Rozbor:
V = 3140 cm3, r = x = ?
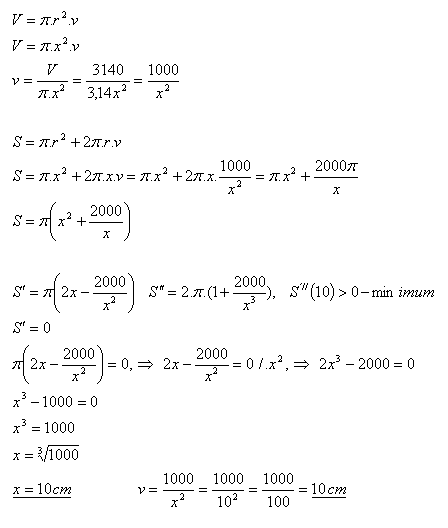
Rozmery nádoby sú r = x = 10cm, v = 10cm.
15. Aké rozmery musí mať obdĺžnik s obvodom O = 40cm, aby jeho uhlopriečka bola minimálna.
Riešenie:
Rozbor:
x = a = ?, b = ?
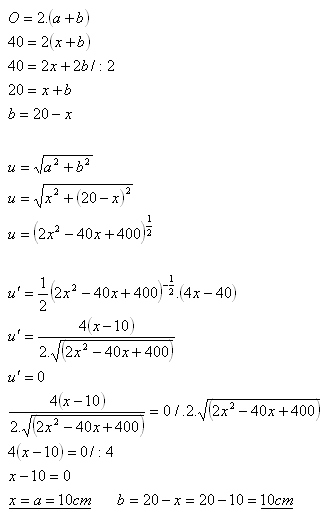
Útvar je štvorec o strane a = 10cm.