Aritmetická postupnosť
1.Charakterizujte vlastnosti aritmetickej postupnosti:
Postupnosť (a2)∞n+1 je aritmetická práve vtedy, ak existuje d є R, že pre všetky n є N platí an+1 = an + d
Číslo d sa nazýva diferencia aritmetickej postupnosti.
V aritmetickej postupnosti platí:
- an = a1 + (n-1)d
- ar = as + (r-s)d
- s = a1 + a2 + a3 + ... + an =
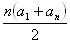
- Ak d > 0 je postupnosť rastúca
- Ak d < 0 je postupnosť klesajúca
- Ak d = 0 je postupnosť konštantná
2.Zistite, či je postupnosť aritmetická:
Riešenie:
a1 = -2, a2 = -1, a3 = 0, a4 = 1, a5 = 2 atď.
Postupnosť je aritmetická s diferenciou d = 1.
3.Napíšte prvých šesť členov aritmetickej postupnosti pre ktorú platí:
a1 + a4 + a6 = 71
a5 – a2 – a3 = 2
Riešenie:
a1 + a1 +3d +a1 +5d = 71
a1 + 4d – a1-d –a1 -2d = 2
3a1 + 8d = 71
-a1 + d =2/3
3a1 + 8d = 71
-3a1 + 3d = 6
a1 – d = -2
a1 = d - 2
a1 = 7 - 2
a1 = 5
11d = 77
d = 7
(a2)n-16 = 5;12;19;26;33;40
4.Napíšte prvých šesť členov aritmetickej postupnosti, v ktorej platí::
Riešenie:
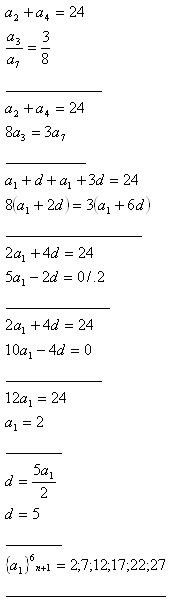
5.Osem čísiel tvorí aritmetickú postupnosť. Určite ich, ak viete, že súčet prostredných členov je 41, súčin krajných je 114.
Riešenie:

6.Medzi korene kvadratickej rovnice x2 – 16x +39 = 0 vložte štyri čísla, aby spolu tvorili aritmetickú postupnosť.
Riešenie:
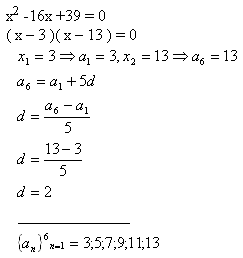
Vložené čísla sú: 5;7;9;11
7.Strany pravouhlého trojuholníka tvoria aritmetickú postupnosť. Dlhšia odvesna má 24 cm. Vypočítajte obvod trojuholníka.
Riešenie:
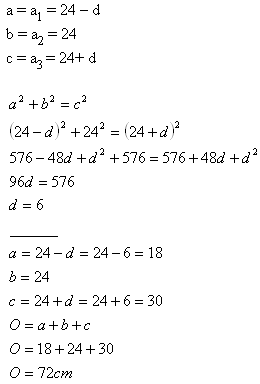
Obvod trojuholníka je 72 cm.
8.Zistite súčet prirodzených čísiel 1+2+3+4+5+6+7+.............+100.
Riešenie:
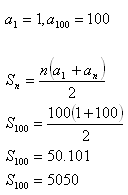
Súčet daných čísiel je S = 5050.
9.Železné rúry sú zrovnané do ôsmych radov tak, že vrchný rad má 13 rúr a každý ďalší o rúru viac. Koľko je všetkých rúr?
Riešenie:
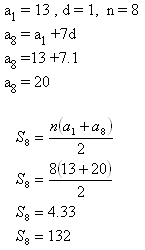
Na hromade je 132 rúr.
10.V trojuholníku uhly tvoria aritmetickú postupnosť. Určite ostatné uhly, ak najmenší uhol má veľkosť 20°.
Riešenie:
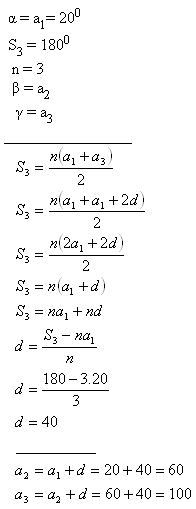
Uhly trojuholníka sú 20°, 60° a 100°.
11.Hrany kvádra tvoria tri po sebe idúce členy aritmetickej postupnosti. Aké sú veľké, ak ich súčet je 24 cm a objem kvádra je 312 cm3?
Riešenie:
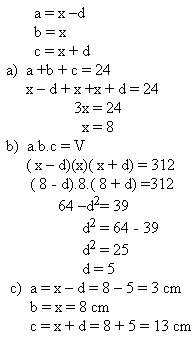
Hrany kvádra majú veľkosť 3 cm, 8 cm a 13cm.
12.Ako dlho by padal kameň do bane v Južnej Amerike hlbokej 2500 m, ak vieme, že v prvej sekunde preletí 4,904 m a za každú ďalšiu o 9,808 m viac?
Riešenie:
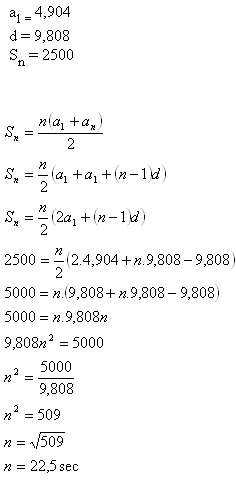
Kameň by do bane padal asi 22,5 sec.