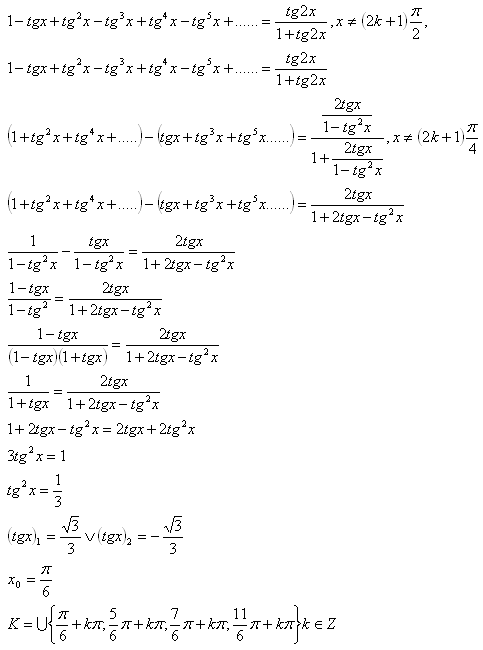Geometrická postupnosť
1.Charakterizujte vlastnosti geometrickej postupnosti:
2.Vypočítajte prvých šesť členov geometrickej postupnosti, ak platí a3 = 8 a a7 = 128.
Riešenie:
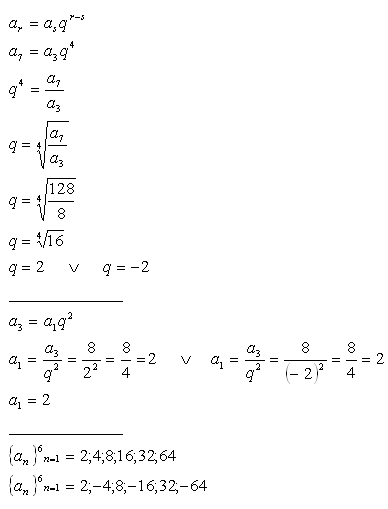
3.Ak pripočítame k číslam 2, 16 a 58 to isté číslo, dostaneme prvé tri členy geometrickej postupnosti. Určite toto číslo a napíšte prvých šesť členov tejto postupnosti.
Riešenie:
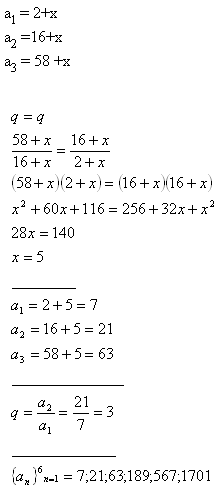
4.Medzi korene rovnice x2 -66x +128 = 0 vložte štyri čísla, aby spolu s koreňmi rovnice tvorili geometrickú postupnosť.
Riešenie:
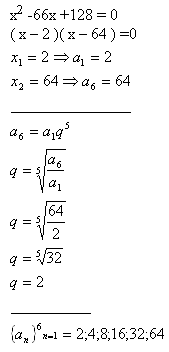
5.Napíšte prvých šesť členov geometrickej postupnosti, pre ktorú platí:
Riešenie:
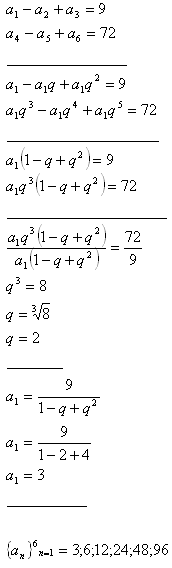
6.Kváder, ktorého hrany tvoria geometrickú postupnosť má povrch S = 78 cm2.
Súčet hrán prechádzajúcich jedným vrcholom je 13 cm. Určite objem kvádra.
Riešenie:
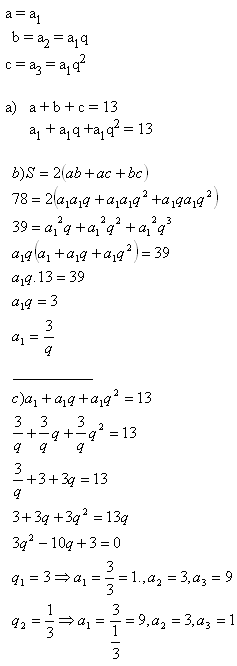
Hrany kvádra sú a = 1cm, b = 3cm, c = 9cm.
Objem kvádra je V = a.b.c
V = 1.3.9 cm
3
V = 27 cm
3
7.Jazdec sa rozhodol kúpiť koňa a zaplatiť zaň 10 000 Sk. S predavačom sa dohodol, že za prvý klinec v podkove zaplatí 1 halier, za druhý 2 haliere, za tretí 4 haliere atď.
Bola to výhodná kúpa, keď každá podkova je pripevnená piatimi klincami?
Riešenie:
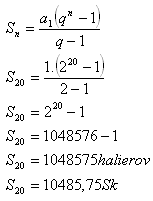
Jazdec preplatil koňa o 485,75 Sk / 16,12 €.
*Na prepočet bol použitý konverzný kurz 1 EUR = 30,1260 SKK
8.Brigádnik súhlasil, že bude pracovať, ak jeho mzda bude za prvý deň 1 Sk, za druhý deň 2 Sk, za tretí deň 4 Sk atď. Koľko dní takto pracoval, ak zarobil 4095 Sk?
Riešenie:
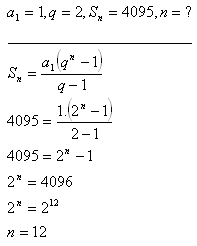
Brigádnik pracoval 12 dní.
9.Na koľko % úrok treba uložiť sumu 10000 Є, aby sme po piatich rokoch mali na účte 25 000 Є?
Riešenie:
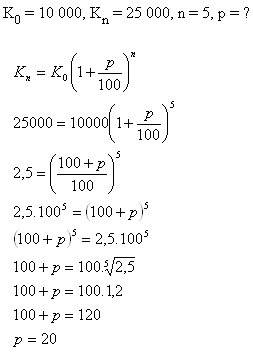
Sumu treba uložiť na 20% úrok.
10.Vypočítajte súčet nekonečného geometrického radu:
Riešenie:
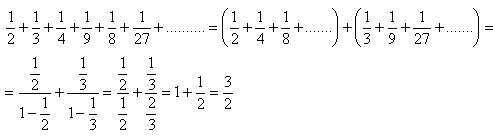
Súčet radu je 3/2.
11. Riešte v R rovnicu:
Riešenie:
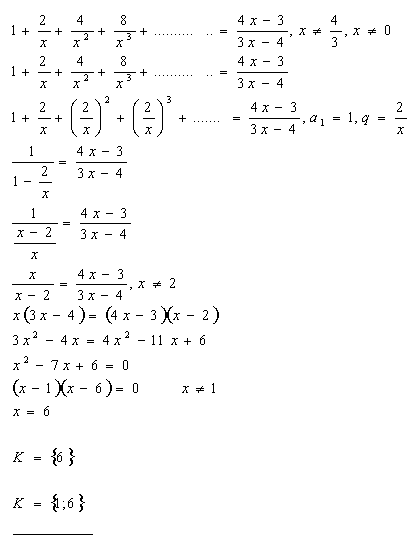
12. Riešte v R rovnicu:
Riešenie: