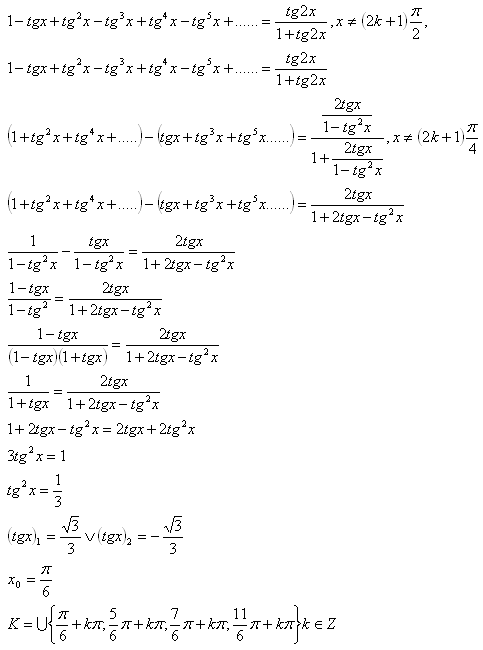Geometrická posloupnost

1.Charakterizujte vlastnosti geometrické posloupnosti.

2.Vypočtěte prvních šest členů geometrické posloupnosti, jestliže platí a₃ = 8 a a₇ = 128.

Řešení:

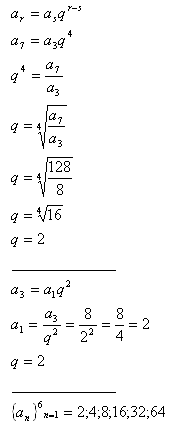
3.Přičteme-li k číslům 2, 16 a 58 stejné číslo, dostaneme první tři členy geometrické posloupnosti. Určete toto číslo a napište prvních šest členů této posloupnosti.

Řešení:

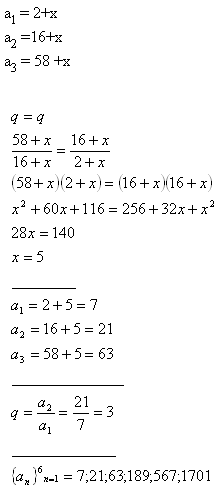
4.Mezi kořeny rovnice x²-66x +128 = 0 vložte čtyři čísla, aby spolu s kořeny rovnice tvořily geometrickou posloupnost.

Řešení:

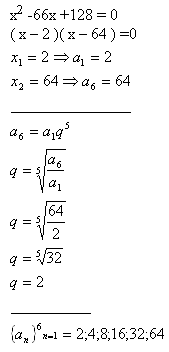
5.Vypočtěte prvních šest členů geometrické posloupnosti, jestliže platí:

Řešení:

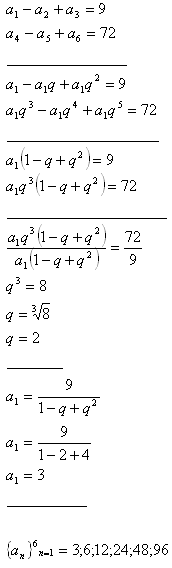
6.Kvádr, jehož hrany tvoří geometrickou posloupnost má povrch S = 78 cm².Součet hran procházejících jedním vrcholem je 13 cm. Určete objem kvádru.

Řešení:

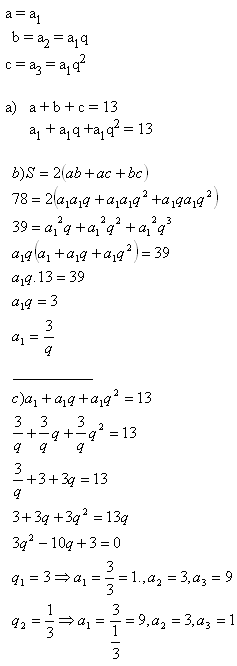
Hrany kvádru jsou a = 1cm, b = 3cm, c = 9cm.
Objem kvádru je V = a.b.c
V = 1.3.9 cm³
V = 27 cm³

7.Jezdec se rozhodl koupit koně a zaplatit za něj 10 000 Sk. S prodavačem se dohodl, že za první hřebík v podkově zaplatí 1 haléř, za druhý 2 haléře, za třetí 4 haléře atd.. Byla to výhodná koupě, když každá podkova je připevněna pěti hřebíky?

Řešení:

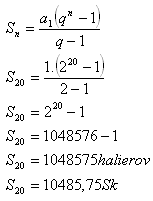
Jezdec proplatil koně o 485,75 Sk / 16,12 €.
* Pro přepočet byl použit konverzní kurz  1 EUR = 30,1260 SKK

8.Brigádník souhlasil, že bude pracovat, pokud jeho mzda bude za první den 1 Kč, za druhý den 2 Kč, za třetí den 4 Sk atd.. Kolik dní takto pracoval, pokud vydělal 4095 Kč?

Řešení:

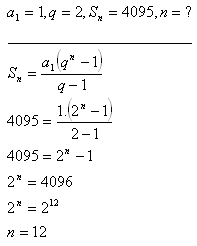
Brigádník pracoval 12 dní.

9.Na kolik% úrok třeba uložit částku 10000 Є, abychom po pěti letech měli na účtu 25 000 Є?

Řešení:

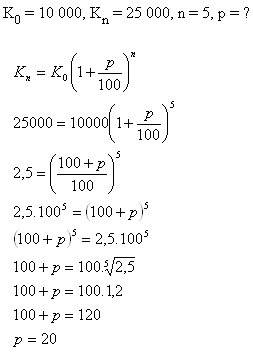
Částku je třeba uložit na 20% úrok.

10.Vypočtěte součet nekonečného geometrického řady:

Řešení:

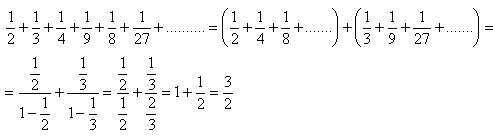
Součet řady je 3/2.

11. Řešte v R rovnici:

Řešení:

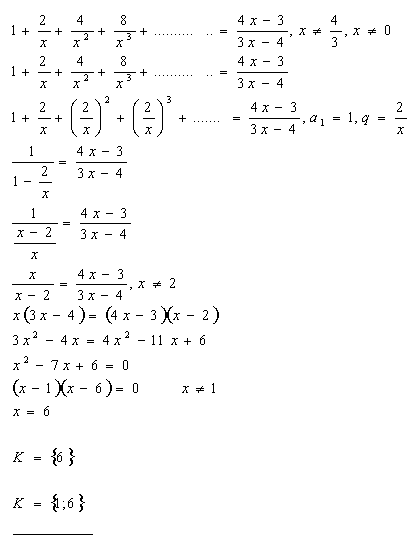
12.Řešte v R rovnici:

Řešení: