Derivace nerozvinuté funkce
1. Jak derivujeme nerozvinutých funkci?
Řešení:
Nechť je dána nerozvinutá - implicitní-funkce F [x; f (x)] = 0. Při jejím derivování derivujeme členy obsahující pouze x obyčejně, členy s y derivujeme jako složené funkce. Jejich derivaci (podle y) vynásobíme y '. Z rovnice vyjádříme y '.
Například:
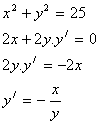
2.Derivujte funkci:
Řešení:
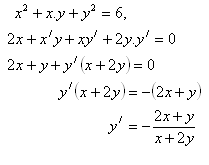
3. Derivujte funkci:
Řešení:
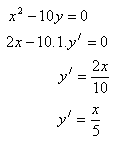
4.Derivujte funkci:
Řešení:
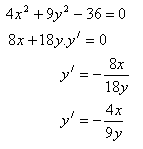
5.Pod jakým úhlem se protínají křivky x2 + y2 – 5 = 0 a y2 – 4x = 0
Řešení:
Úhel protínajících se křivek je roven úhlu jejich tečen ve společném bodě T. Společný bod T:
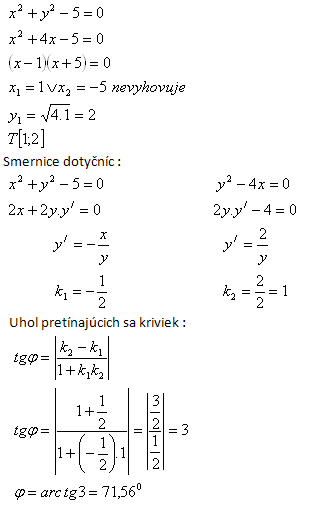
6.Zderivujte funkci x3 + y3 -3axy = 0
Řešení:
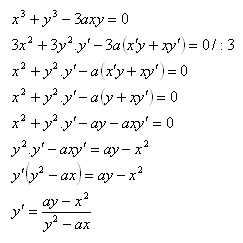
7.Zderivujte funkci ey + e–x + xy = 0
Řešení:
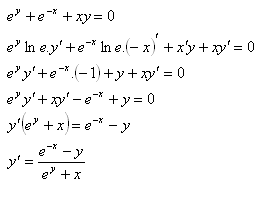
8.Vypočtěte první derivaci funkce exy-x2+y3=0 pre x=0
Řešení:
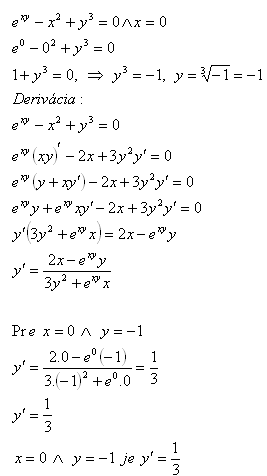
9.Napište rovnici tečny ke kružnici x2 + y2 + 4x – 4y +3 = 0 v bodě, ve kterém kružnice protíná x - ovou souřadnicovou osu.
Řešení:
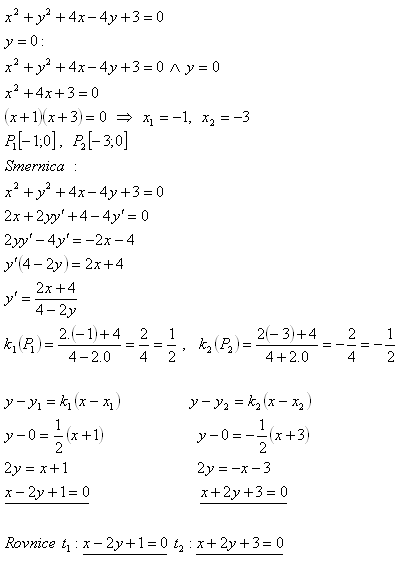
10.Napište rovnici tečny ke křivce:
Řešení:
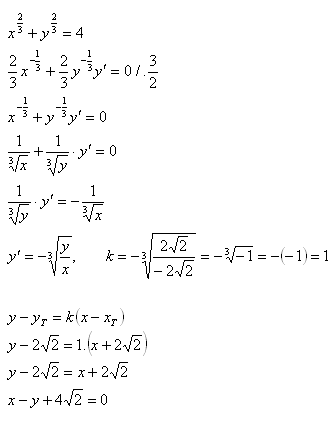
Rovnici tečny je x – y + 4√2 = 0