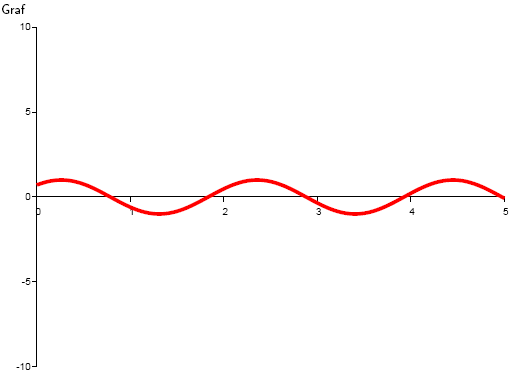
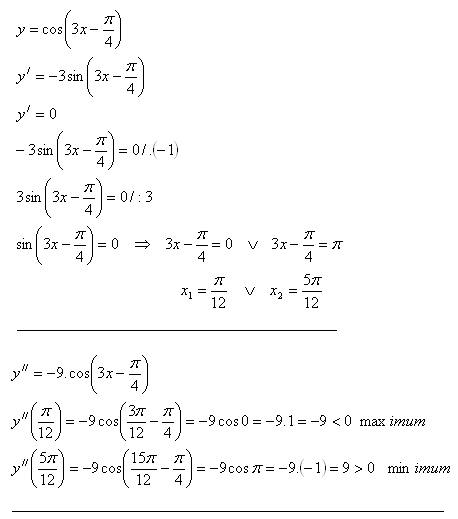Průběh funkce
1. Jak zjišťujeme průběh funkce?
Řešení:
a.) Funkce y = f(x) je v bodě x0 rostoucí pokud f‘(x0) > 0
b.) Funkce y = f(x) je v bodě x0 klesající pokud f‘(x0) < 0
c.) Funkce y = f(x) má v bodě x0 stacionární bod pokud f‘(x0) = 0
d.) Funkce y = f(x) je v bodě x0 vypouklá pokud f‘‘(x0) > 0
e.) Funkce y = f(x) je v bodě x0 vydutá pokud f‘‘(x0) < 0
f.) Funkce y = f(x) má v bodě x0 inflexní bod pokud f‘‘(x0) = 0 ^ f‘‘(x0) <> 0
g.) Funkce y = f(x) má v bodě x0 lokální minimum pokud f‘ (xo) =0 ^ f‘‘ (xo) >0
h.) Funkce y = f(x) má v bodě x0 lokální maximum pokud f‘ (xo) =0 ^ f‘‘ (xo) <0
2. Daná je funkce y = x3 – 5x2 + 3x -5. Určete pro které x je funkce rostoucí, klesající, vypouklá a vydutá.
Řešení:
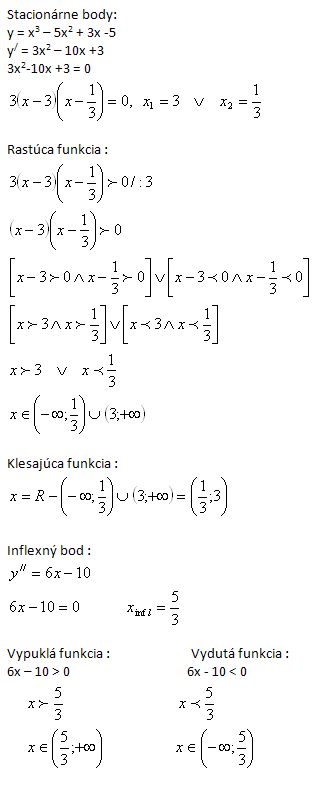
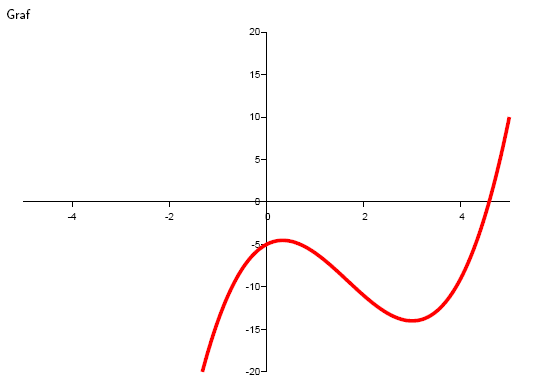
3.Zjistěte zda funkce y = x3 -5x2 +3x -5 je v bodě x0 = 2 klesající a vypuklá.
Řešení:
y = x3 -5x2 +3x -5
y‘ = 3x2 -10x +3
y‘(2) =3.22 -10.2 +3
y‘(2) = -5 < 0
Funkcia je klesajíc .
y‘ = 3x2 -10x +3
y‘‘ = 6x-10
y‘‘(2) = 6.2 – 10
y‘‘(2) = 2 > 0
Funkcia je vypuklá.

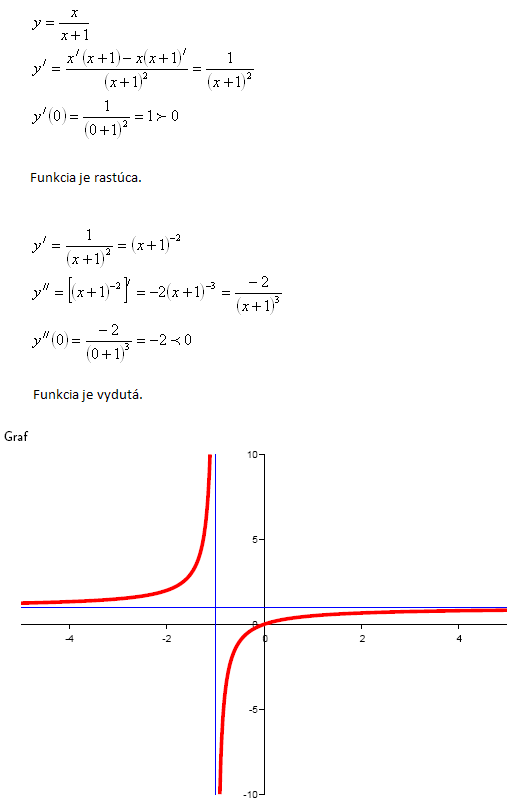
4.Zjistěte zda je funkce v okolí bodu x0 = 0 rostoucí a vydutá.
Řešení:
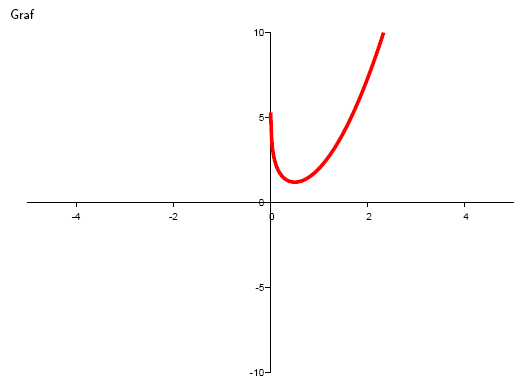
5.Daná je funkce y = 2x2 – ln x. Určete pro které x funkcia klesá.
Řešení:

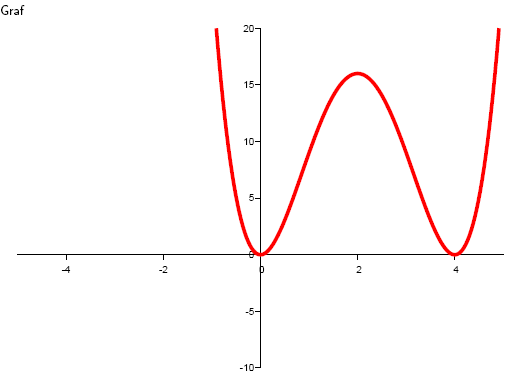
6. Určete lokální extrémy funkce y = x2(4 – x )2
Řešení:
Lokální extrémy:
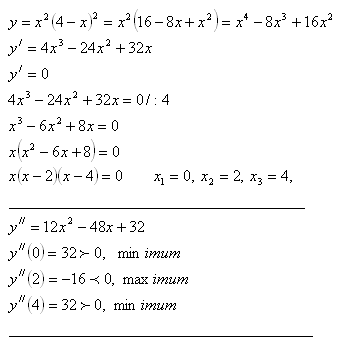
Funkce má v bodě x1 = 0 a x3 = 4 lokální minimum a v bode x2 = 2 maximum.
7. Určete lokální extrémy funkce y = sin x.(1+cos x) pro
Řešení:
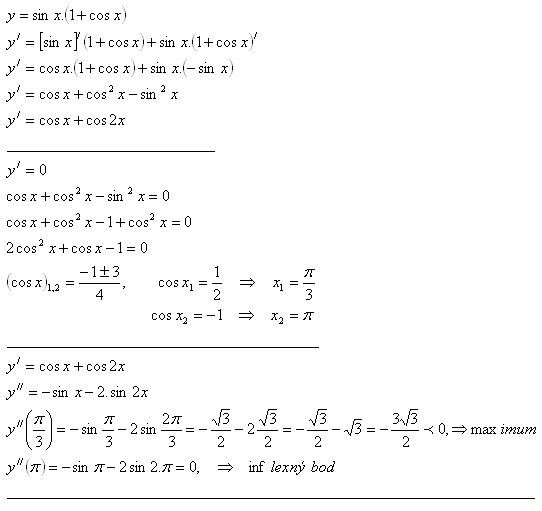
8.Zjistěte stacionární body a intervaly vzrůstu a poklesu funkce:
Řešení:

9.Pro které hodnoty a, b je bod I [1; 3] inflexním bodem funkce y = ax3 +bx2 ?
Řešení:
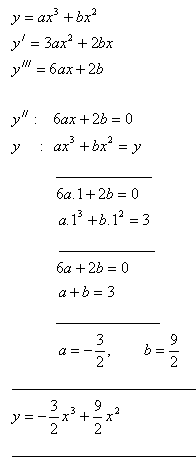
10. Najděte lokální extrémy funkce:
Řešení: