Permutace
1. Definujte a charakterizujte:
a) Permutace z n prvků
b) Permutace z n prvků s opakováním
Řešení:
Permutace
Permutace n prvků je každá uspořádaná n-tice vytvořená z těchto prvků.
Každý zn prvků se v této n-tici vyskytuje právě jednou. Jednotlivé permutace se od sebe liší pouze pořadím prvků.
P(n) = n!
Permutace s opakováním
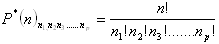
n
1 – počet stejných prvků 1. druhu
n
2 - počet stejných prvků 2. druhu
n
3 - počet stejných prvků 3. druhu, atd
n
j - počet stejných prvků j-tého druhu
Platí : n
1+n
2+n
3+.........+n
j = n
2. Dané jsou tři prvky a, b, c. Vytvořte z nich:
a) permutacie (bez opakování)
b) permutacie s opakováním, v nichž se "a" vyskytne 2 krát, "b" jednou a "c" jednou
Řešení:
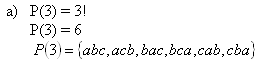
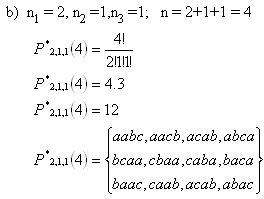
3. Kolik různých päťciferných přirozených čísel lze napsat pomocí číslic 1,2,3,4,5, pokud:
- a) číslice v čísle použije jen jednou?
- b) Kolik z napsaných čísel bude začínat číslicí 5?
- c) Kolik z napsaných čísel bude sudých?
Řešení:
a) P(5) = 5! = 5.4.3.2.1 = 120
b) P(4) = 4! = 4.3.2.1 =24
c)
končících 2: P(4) = 4! =24
končících 4: P(4) = 4! = 24
spolu : S = 2.4! = 2.24 = 48
4. Osm studentů má na internátě připraveno ubytování ve třech pokojích. Dvě jsou třílůžkové a jedna Dvoulužkový. Kolik je způsobů rozdělení studentů do pokojů?
Řešení:
První pokoj: n
1 = 3
Druhý pokoj: n
2 = 3
Třetí pokoj: n
3 = 2
n = 3 + 3 + 2 = 8
Existuje 560 způsobů rozdělení studentů do pokojů.
5. Kolika způsoby je možné hodit třemi kostkami součet 11?
Řešení:
a) permutace trojice 6,4,1 : P(3) = 3! = 6
b) permutace trojice 6,3,2 : P(3) = 3! = 6
c) permutace trojice 5,5,1 : P2,1*(3) = 3
d) permutace trojice 5,4,2 : P(3) = 3! = 6
e) permutace trojice 5,3,3 : P*1,2(3) = 3
f) permutace trojice 4,4,3 : P*2,1(3) = 3
Spolu 6+6+3+6+3+3 = 27 způsobú.
6.Čtyři české a tři slovenské knihy třeba uspořádat na poličce tak, aby byly seřazeny nejprve české a poté slovenské knihy. Kolik je způsobů jak se to dá udělat?
Řešení:
Usporiadanie českých knih: P(4) = 4! =24
Usporiadanie slovenských knih: P(3) = 3! = 6
N = P(4).P(3) = 24.6 = 144
Knihy sa dajú usporiadať 144 spôsobmi.
7. Pokud se zvětší počet prvků o 2, zvětší se počet permutací (bez opakování) 42 krát.
Kolik prvků na to potřebujeme?
Řešení:
P(x + 2) = 42.P(x)
(x + 2)! = 42.x!
(x + 2)(x +1)x! = 42x!/: x!
(x + 2)(x + 1) = 42
x2 + 3x +2 - 42 = 0
x2 +3x – 40 = 0
(x – 5)(x + 8) = 0
x1 = 5
x2 = - 8 nevyhovuje
K={5}
Potrebujeme 5 prvkov.
8. Patnáct svatebčanú se nemohlo dohodnout, kdo kde bude stát na svatební fotografii.
Ženich navrhl, aby učinily všechny možné sestavy svatebčanů na fotografiích.
- a) Kolik fotografií je třeba udělat?
- b) Kolik by fotografování trvalo, kdyby vyfotografování jedné fotky trvalo 10 sekund a fotografovali by se den i noc?
Řešení:
a)
P(15) = 15! = 1,307.10
12
Je třeba udělat 1,307.10
12 fotografií.
b)
Fotografování by trvalo 414 377 let.
9. Šestimístné kód uzavírání trezoru v bance je vytvořen ze stejných číslic jako číslo 926002.
Kolik je možností vytvoření příslušného kódu?
Jaký čas by trvalo zloději vytočit všechny možnosti, pokud vytočit jeden kód mu trvá 5 sekund?
Řešení:
n
1 = 2, n
2 = 2, n
3 = 1, n
4 = 1, n = 6
t = 180.5sec. = 900 sec. = 15 minút
Možností je 180 a zloději by to trvalo 15 minut (jestliže správný je až poslední vytočený kód).
10. Student, který se hlásí na vysokou školu musí udělat 4 zkoušky. Za každou úspěšně vykonané zkoušce obdrží podle obtížnosti 2,3 nebo 4 body. K přijetí stačí dosáhnout 13 bodů. Kolika způsoby může student udělat zkoušky, aby byl přijat?
Řešení:
Aby byl student přijat musí získat 13, 14, 15 nebo 16 bodů.
| 13 bodů: |
(3,3,3,4) |
P*3,1(4) = 4 |
| |
(4,4,3,2) |
P*2,1,1(4) = 12 |
| 14 bodů: |
(4,4,4,2) |
P*3,1(4) = 4 |
| |
(4,4,3,3) |
P*2,2(4) = 6 |
| 15 bodů: |
(4,4,4,3) |
P*3,1(4) = 4 |
| 16 bodů: |
(4,4,4,4) |
P*4(4) = 1 |
N = 4 + 12 + 4 + 6 + 4 + 1 = 31
Student má celkem 31 možností jak získat požadované body.