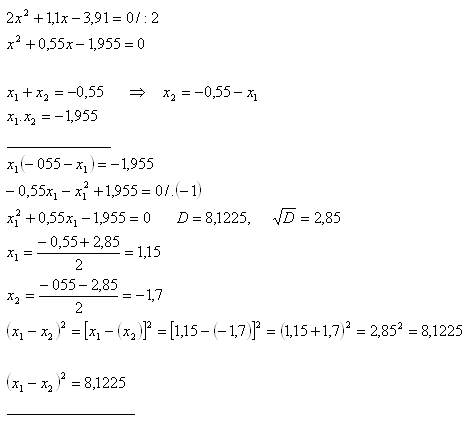Vlastnosti kořenů kvadratické rovnice
1. Zostavte kvadratickou rovnici x2 +px +q = 0 pokudp = -(x1+x2) a q = x1.x2 :
Řešení:
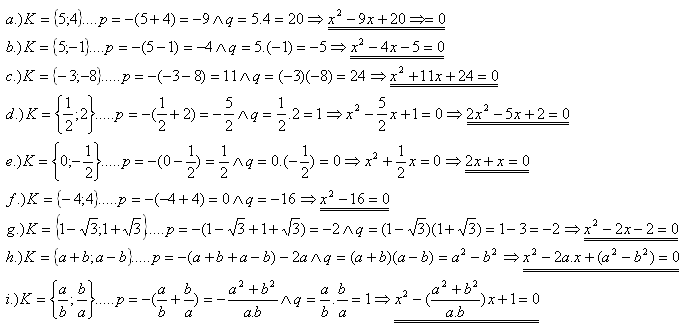
2. Určete číslo „k“ tak, aby jeden kořen rovnice x2-5x+k=0 byl x1=3
Řešení:
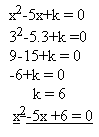
3. Určete číslo „k“ tak, aby jeden kořen rovnice kx2-15x+7=0 byl x1=7
Řešení:
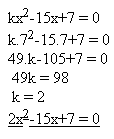
4.Určete číslo „k“ tak, aby jeden kořen rovnice x2+kx+20=0 byl x1=10
Řešení:
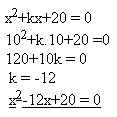
5.Určete číslo „a“ tak, aby pro kořeny rovnice platilo x2-3ax-4a2=0 a x1-x2=10
Řešení:
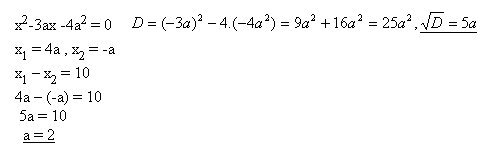
6. Pro která reálne čísla „m“ má rovnice x2+3x-2m2+m+3=0 jeden kořen rovný nule? Vypočtěte druhý kořen rovnice.
Řešení:
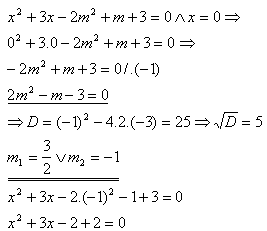
7. Daná je rovnice x2-13x+36=0. Napište rovnici s kořeny y1,y2 pro ktoré platí:
Řešení:
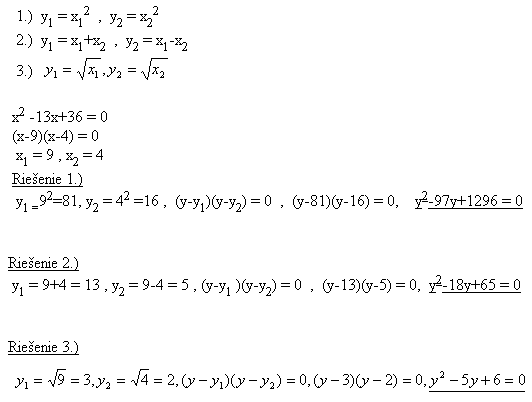
8. Daná je rovnice x2 – 6x +8 = 0. Zostavte rovnici pro kořeny které platí:
Řešení:
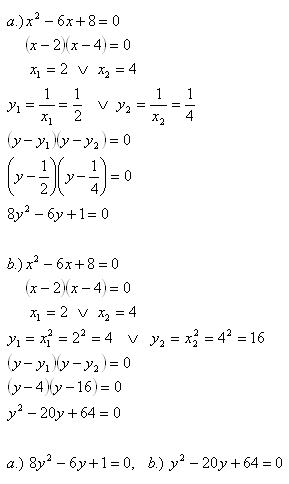
9. Rovnice x2–x .cos α + cos 2α = 0 má kořeny x1 , x2. Vyjádřete výraz
Řešení:
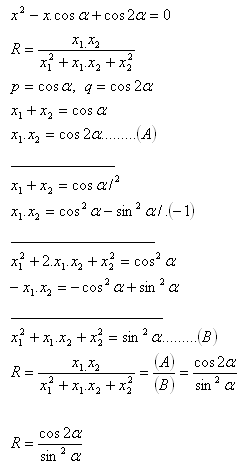
10. Jesli x1 a x2 jsou kořeny rovnice 2x2 + 1,1x - 3,91 = 0, vypočítejte (x1 – x2)2, rovnicu neriešte.
Řešení: