Výroky
1.Charakterizujte základní vlastnosti výroků.
Řešení:
Výrok je každá oznamovací věta, o níž má smysl uvažovat zda je pravdivá nebo nepravdivá. Výroky označujeme: A, B, C, D, V, ... atd..
Výrok
- a) pravdivý - "platí" má pravdivostní hodnotu (1)
- b) nepravdivý - "neplatí" má pravdivostní hodnotu (0)
Negace výroku
Ke každému výroku A lze vytvořit výrok A ', který popírá (neguje) to, co tvrdí výrok A. Výrok A 'se nazývá negace výroku A. Negaci vytvoříme tak, že před výrok dáme předponu "ne ..", "není", nebo text "není pravda že ....".
2.K daným výrokem vytvořte jejich negace. Určitě pravdivosti hodnoty původních a negován výroků.
A: Číslo 3 je prvočíslo (1)
B: Bratislava leží v Egyptě (0)
C: Prešovský kraj
D: Matematika je věda (1)
E: Číslo 22 je dělitelné 2 (1)
F: Dobrý den!
G: Existuje sněžný muž Yetti
H: Sinus 300 je - 2,1 (0)
I: Máš domácí úkol?
J: x2 -5x +6 = 0
K: Číslo 2574364 je dělitelné 4 (1)
L: Platí že (a + b)2 = a2 + b2 (0)
M: Obsah kruhu je S = π.r2 (1)
N: 42 sa rovná 18 (0)
O: Mám nové auto (1)
P: Není zde.
Řešení:
A ': Číslo 3 není prvočíslo (0
)B ': Bratislava neleží v Egyptě (1)
C: není výrok
D ': Matematika není věda (0)
E ': Číslo 22 není dělitelné 2 (0)
F: není výrok
G: nedá se rozhodnout
H ': Sinus 300 není -2,1 (1)
I: není výrok
J: není výrok
K ': Číslo 2574364 není dělitelné 4 (0)
L': Neplatí že ( a + b )2 = a2 + b2 (1)
M': Obsah kruhu není S = π.r2 (0)
N': Není pravda, že 42 se rovná 18 (1)
O': Nemám nové auto (0)
P : není výrok
3.Zopakujme si vlastnosti kvantifikovaného výroku.
Řešení:
Kvantifikovaný výrok je oznamovací věta, která udává určitý počet, nebo odhad počtu předmětů, osob atd.. se stejnou vlastností. V kvantifikovaných výroku se vyskytují slova: právě, nejvíce, každý, všichni, někteří, alespoň, žádný ... atd.., Které se nazývají kvantifikátor a číslovky.
Výrok "alespoň 5" znamená 5 a více.
Výrok "nejvíce 5" znamená 5 a méně
Pro symbolické zápisy kvantifikovaných výroků používáme:
- a) všeobecný kvantifikátor
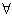- "pro každé (všechny) platí ....."
- b) existenční kvantifikátor
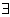- "existuje alespoň jedno ..., pro které platí ...."
Negace kvantifikovaného výroku
Každý ... je ...
|
Alespoň jeden ... není ...
|
Alespoň jeden ... je ...
|
Každý ... není ...
|
Alespoň n ... je ...(n>1)
|
Nejvíce (n-1)... je ...
|
Nejvíce n ... je ... (n>=1)
|
Alespoň (n+1)... je ...
|
Právě n ... je ...
|
Nejvíce (n-1) anebo alespoň (n+1) je... |
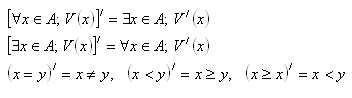
4. Negujte následující výroky:
A: Číslo 3 je kořenem rovnice x2 = 9 (1)
B : 23 -5 > 7 (0)
C: Úhlopříčky čtverce jsou na sebe kolmé (1)
D: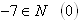 
E: Každá úloha má řešení (0)
F: Existuje alespoň jeden obdélník, který má kolmé úhlopříčky (0)
G: Existuje alespoň jeden pravoúhlý trojúhelník (1)
H: Tato kniha má nejvíce 50 stran (1)
I: Každá píseň má konec (1)
J: Na zasedání ZRPŠ bylo právě 20 rodičů (0)
K: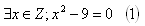 
L: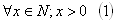 
Řešení:
A‘: Číslo 3 není kořenem rovnice x2 = 9 (0)
B‘: 23 -5 <= 7
C‘: Úhlopříčky čtverce nejsou na sebe kolmé (0)
D‘: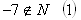 
E ': Existuje alespoň jedna úloha, která nemá řešení (1)
F ': Všechny obdélníky nemají kolmé úhlopříčky (1)
G ': Všechny trojúhelníky jsou nepravoúhlé (0)
H ': Tato kniha má alespoň 51 stran (0)
I ': Existuje alespoň jedna píseň, která nemá konec (0)
J ': Na zasedání ZRPŠ bylo nejvíce 19 nebo alespoň (nejméně) 21 rodičů (1)
K‘: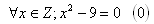 
L‘: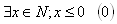 
5. Co víme o složených výrocích?
Řešení:
6.Negujte následující výroky (SK):
A: Príde Peter a Mária
B: Prší a je mokro
C: Svieti slnko alebo fúka vietor
D: Ak sa nahneváme, budeme zlí
E: Ak príde Jozef, potom príde aj Eva
F: Mám dobrú náladu práve vtedy, keď prší
G: Každý lichobežník je rovnostranný
H: Existuje aspoň jedno prvočíslo, ktoré je párne
I: V triede 1.A aspoň 8 žiakov nosí okuliare
J: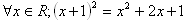 
Řešení:
A‘: Nepríde Peter alebo Mária
B': Neprší alebo nie je mokro
C': Nesvieti slnko a nefúka vietor
D': Nahneváme sa a nebudeme zlí
E': Jozef príde a Eva nepríde
F': Mám dobrú náladu a neprší alebo nemám dobrú náladu a prší
G': Existuje aspoň jeden lichobežník, ktorý nie je rovnostranný
H': Všetky prvočísla sú nepárne
I': V triede 1.A najviac 7 žiakov nosí okuliare
J‘: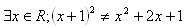 
7. Z daných výrokov A, B vytvorte:
Řešení:
8.Dané jsou výroky P: prší, S: svítí Slunce, V: fouká vítr. Vytvořte z nich složené výroky
Řešení:
P‘: Neprší
9.Zjistěte pomocí tabulky pravdivostní hodnotu formule:
Řešení:
Formula platí. Je to tautológie.
Totožnostno-pravdivý výrok nebo tautologie (z řeckého ταυτολογία tautologie) je výrok, výraz nebo formule logického kalkulu, která je pravdivá při jakýchkoliv významech pravdivosti jejich proměnných.