Statements
1.Characterize the basic properties of statements.
Solution:
A statement is any declarative sentence for which it makes sense to consider whether it is true or false. We denote statements by: A, B, C, D, P, ... etc.
Statement
- a) true – “holds,” has the truth value (1)
- b) false – “does not hold,” has the truth value (0)
Negation of a statement
For every statement A, we can form a statement A‘ that denies (negates) what statement A asserts. Statement A‘ is called the negation of statement A. We form the negation by putting before the statement a prefix like “not ...,” “is not,” or the text “it is not true that ....”
2.Create negations for the given statements. Determine the truth values of the original and negated statements.
A: The number 3 is a prime number (1)
B: Bratislava lies in Egypt (0)
C: Prešov Region
D: Mathematics is a science (1)
E: The number 22 is divisible by 2 (1)
F: Good day!
G: The abominable snowman Yeti exists
H: Sine of 300 is –2.1 (0)
I: Do you have homework?
J: x2 - 5x + 6 = 0
K: The number 2574364 is divisible by 4 (1)
L: It holds that (a + b)2 = a2 + b2 (0)
M: The area of a circle is S = π·r2 (1)
N: 42 equals 18 (0) equals 18 (1)
O: I have a new car (1)
P: He/She is not here.
Solution:
A': The number 3 is not a prime number (0)
B': Bratislava does not lie in Egypt (1)
C : not a statement
D': Mathematics is not a science (0)
E': The number 22 is not divisible by 2 (0)
F : not a statement
G : cannot be decided
H': Sine of 300 is not −2.1 (1)
I : not a statement
J : not a statement
K': The number 2574364 is not divisible by 4 (0)
L': It is not true that (a + b)2 = a2 + b2 (1)
M': The area of a circle is not S = π·r2 (0)
N': It is not true that 42 equals 18 (1)
O': I do not have a new car (0)
P : not a statement
3.Let’s review the properties of a quantified statement.
Solution:
A quantified statement is a declarative sentence that gives a certain number, or an estimate of the number, of objects, persons, etc., with the same property. In a quantified statement we encounter words such as: exactly, at most, every, all, some, at least, none ... etc., which are called quantifiers, as well as numerals.
- The statement “at least 5” means 5 or more.
- The statement “at most 5” means 5 or less.
For symbolic notation of quantified statements we use
- a) the universal quantifier
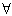 – “for every (all) it holds that.....”
– “for every (all) it holds that.....”
- b) the existential quantifier
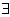 – “there exists at least one ... for which it holds that ....”
– “there exists at least one ... for which it holds that ....”
Negation of a quantified statement
Every ... is ...
|
At least one ... is not ...
|
At least one ... is ...
|
Every ... is not ...
|
At least n ... are ... (n>1)
|
At most (n−1) ... are ...
|
At most n ... are ... (n>=1)
|
At least (n+1) ... are ...
|
Exactly n ... are ...
|
At most (n−1) or at least (n+1) ... are ... |
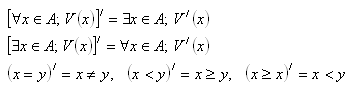
4. Negate the following statements:
A: The number 3 is a root of the equation x2 = 9 (1)
B : 23 − 5 > 7 (0)
C: The diagonals of a square are perpendicular to each other (1)
D: 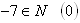
E: Every problem has a solution (0)
F: There exists at least one rectangle whose diagonals are perpendicular (0)
G: There exists at least one right triangle (1)
H: This book has at most 50 pages (1)
I: Every song has an ending (1)
J: There were exactly 20 parents at the PTA meeting (0)
K: 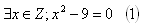
L: 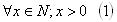
Solution:
A‘: The number 3 is not a root of the equation x2 = 9 (0)
B‘: 23 − 5 <= 7
C‘: The diagonals of a square are not perpendicular to each other (0)
D‘: 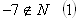
E‘: There exists at least one problem that has no solution (1)
F‘: All rectangles do not have perpendicular diagonals (1)
G‘: All triangles are non-right (0)
H‘: This book has at least 51 pages (0)
I‘: There exists at least one song that has no ending (0)
J‘: There were at most 19 or at least (no fewer than) 21 parents at the PTA meeting (1)
K‘: 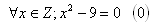
L‘: 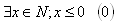
5. What do we know about compound statements?
Solution:
Compound statements arise from the connection of two simple statements A, B.
The compound statements are:
a) Conjunction ∧
b) Disjunction ∨
c) Implication ⇒
d) Equivalence ⇔
a) Conjunction
A conjunction of two statements arises from their connection with “and”, “as well”, or “at the same time”.
The conjunction is true if both statements are true at the same time.
b) Disjunction
A disjunction of two statements arises from their connection with “or”.
The disjunction is true if at least one of the statements is true.
c) Implication
An implication of two statements arises by placing the word “if” before the first statement, and the word “then” before the second statement.
The implication is false only if truth implies falsehood (by convention).
d) Equivalence
An equivalence of two statements arises from their connection with “if and only if”.
The equivalence is true exactly when both statements have the same truth value.
Truth Table
| A |
B |
A ∧ B |
A ∨ B |
A ⇒ B |
A ⇔ B |
| 1 |
1 |
1 |
1 |
1 |
1 |
| 1 |
0 |
0 |
1 |
0 |
0 |
| 0 |
1 |
0 |
1 |
1 |
0 |
| 0 |
0 |
0 |
0 |
1 |
1 |
Negation of compound statements
6.Negate the following statements:
A: Peter and Mária will come
B: It is raining and it is wet
C: The sun is shining or the wind is blowing
D: If we get angry, we will be bad
E: If Jozef comes, then Eva will come as well
F: I am in a good mood if and only if it is raining
G: Every trapezoid is equilateral
H: There exists at least one prime number that is even
I: In class 1.A at least 8 students wear glasses
J: 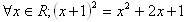
Solution:
A‘: Either Peter or Mária will not come
B': It is not raining or it is not wet
C': The sun is not shining and the wind is not blowing
D': We get angry and we will not be bad
E': Jozef comes and Eva does not come
F': I am in a good mood and it is not raining, or I am not in a good mood and it is raining
G': There exists at least one trapezoid that is not equilateral
H': All prime numbers are odd
I': In class 1.A at most 7 students wear glasses
J‘: 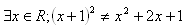
7. From the given statements A, B create:
Solution:
A: The number 20 is odd (0)
B: The number 20 ends with zero (1)
A ∧ B: The number 20 is odd and ends with zero. (0)
A ∨ B: The number 20 is odd or ends with zero. (1)
A ⇒ B: If the number 20 is odd, then it ends with zero. (1)
A ⇔ B: The number 20 is odd if and only if it ends with zero. (0)
A: The diagonals of a rectangle are equal in length (1)
B: The diagonals of a rectangle are perpendicular to each other (0)
A ∧ B: The diagonals of a rectangle are equal in length and are perpendicular to each other. (0)
A ∨ B: The diagonals of a rectangle are equal in length or are perpendicular to each other. (1)
A ⇒ B: If the diagonals of a rectangle are equal in length, then they are perpendicular to each other. (0)
A ⇔ B: The diagonals of a rectangle are equal in length if and only if they are perpendicular to each other. (0)
8.Given the statements P: it is raining, S: the Sun is shining, V: the wind is blowing. Create compound statements from them
Solution:
P‘: It is not raining
P ∧ V′: It is raining and the wind is not blowing
(P ∨ S′)′: It is not true that it is raining or the sun is not shining
(P ∧ V) ⇒ S′: If it is raining and the wind is blowing, then the sun is not shining
P′ ∧ S′: It is not raining and the sun is not shining
(P ∧ S) ⇔ V′: It is raining and the sun is shining if and only if the wind is not blowing
V ⇒ S′: If the wind is blowing, then the sun is not shining
(P ∧ S) ⇒ V′: If it is raining and the sun is shining, then the wind is not blowing
(P ∨ S) ⇔ V′: It is raining or the sun is shining if and only if the wind is not blowing
(P ∧ S) ∨ (P ∧ V′): It is raining and the sun is shining, or it is raining and the wind is not blowing
S ⇒ (P′ ∧ V′): If the sun is shining, then it is not raining and the wind is not blowing
(P′ ∨ S) ⇔ V: It is not raining or the sun is shining if and only if the wind is blowing
(P ∧ S)′: It is not true that it is raining and the sun is shining
(S′ ∧ P) ⇒ V: If the sun is not shining and it is raining, then the wind is blowing
(P′ ∧ V′) ⇒ S: It is not true that if it is not raining and the wind is not blowing, then the sun is shining
9.Determine using a truth table the truth value of the formula:
Solution:

The formula holds. It is a tautology.
A tautology is a statement, expression, or formula of a logical calculus that is true for any truth values of its variables.