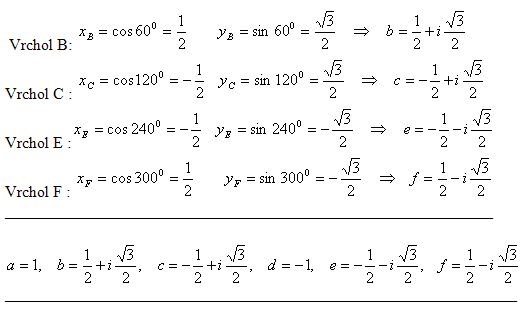Properties of complex numbers
1.Given complex numbers a = 1+2i , b = 2 – i. Determine a + b, a – b, a·b, a / b, |a|, further
Determine whether the number
is a complex unit.
Solution:
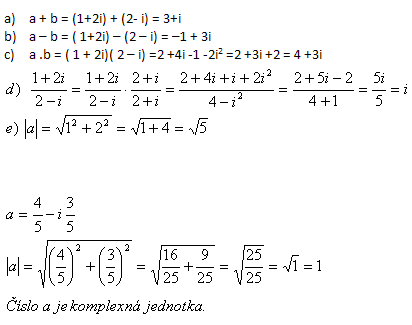
2.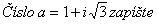
- a) in trigonometric form
- b) in exponential form
- c) calculate a5
- d) calculate √a
Solution:
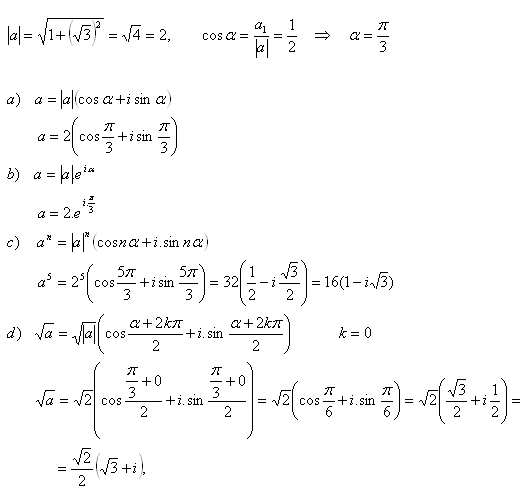
3.Calculate:
Solution:
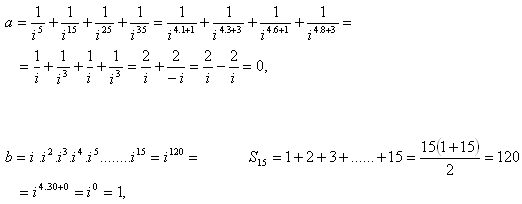
4.Calculate:
Solution:
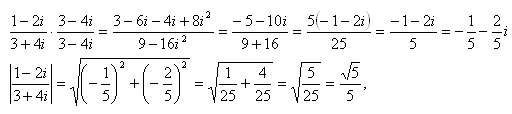
5.Find real numbers x , y such that:
(3 – 2i)·x + (5 – 7i)·y = 1 + 3i
Solution:
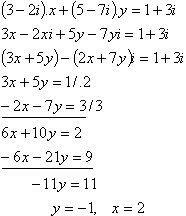
6.Calculate:
Solution:
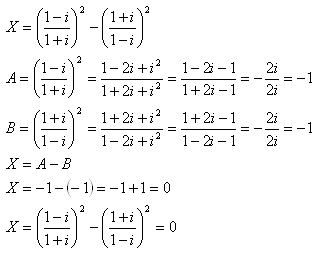
7. A square has its center at the origin of the Gaussian plane, one vertex is the image of the complex number a=4 + 3i.
- a) Which complex numbers represent the remaining vertices
- b) Determine the area of this square
Solution:

8.Calculate the length of the median tc of triangle ΔABC, if its vertices A,B,C are the images of the complex numbers a = –1 –i , b = –5 + 7i , c = 9 + 8i.
Solution:
The length of the median tc is the length of the segment CS, where S is the midpoint of segment AB
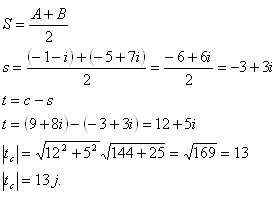
The median tc has length 13 u.
9.A regular hexagon ABCDEF has center S at the origin of the Gaussian plane and vertex A at the image of the complex unit on the real axis. Determine the complex numbers whose images are at the other vertices of the hexagon.
Solution:
Vertex A : a = 1
Vertex D : d = –1
The other vertices lie in individual quadrants of the Gaussian plane.
Triangle Δ SAB is equilateral SA = SB = AB = 1