Sieve of Eratosthenes

From the set of natural numbers N, it is possible to select a subset that has troubled mathematicians for centuries. It is the set of prime numbers. By definition, a prime number is a natural number that is divisible only by one and itself. The number one is not considered a prime. The first problem is how to select the set of prime numbers from the set N. This question was successfully solved by ERATOSTHENES of Cyrene (275 – 195 BC), a Greek mathematician. He developed a method of gradually eliminating composite numbers. This method was named the Sieve of Eratosthenes.

The method consists of the following:

We write down several natural numbers, for example 1 – 20. We skip one, circle two, and underline every second number starting from two. We circle three and underline every third number starting from three. We circle five and underline every fifth number starting from five, and so on. Some numbers will be underlined multiple times. The circled numbers are prime numbers.

 

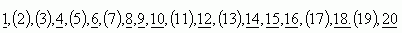
In the first twenty natural numbers, there are 8 prime numbers: 2, 3, 5, 7, 11, 13, 17, 19. Using this method, prime numbers lying between 1 and 10,000,000 were determined. Diligent calculators worked out all the prime numbers in this interval and found that there are exactly 664,579 primes. Prime numbers are arranged in various tables. There are even tables stored on microfilms containing 6 million prime numbers, with the largest being 104,395,301.

Literature: Opava, Z.: Mathematics Around Us, Prague, Albatros 1989

---