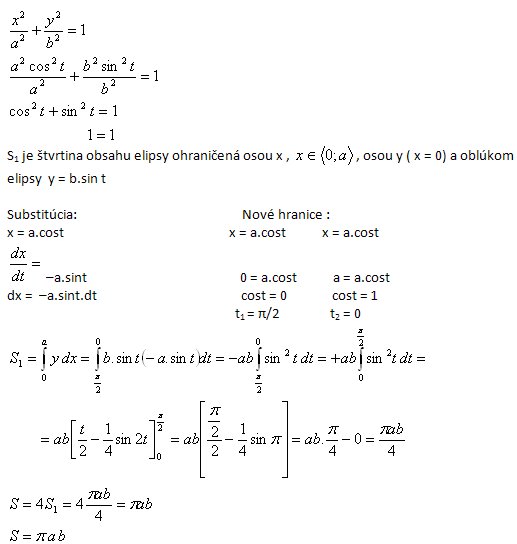Squaring
1.Explain the term “quadrature”
Solution:
Quadrature is the calculation of the area of a plane figure that is bounded by the x-axis, two lines parallel to the y-axis at the points x1 = a, x2 = b, and a line (straight or curved) with the equation y = f(x).
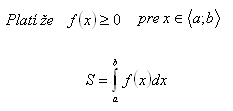
2.Using a definite integral, derive the formula for calculating the area of
Solution:
a) Square
The square is bounded by the x-axis, the line y = a, and lines parallel to the y-axis at the points a = 0, b = a.
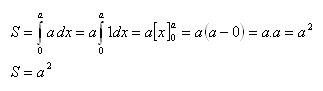
b) Rectangle
The rectangle is bounded by the x-axis, the line y = b, and lines parallel to the y-axis at the points a = 0, b = a.
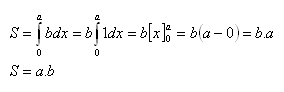
3.Using a definite integral, derive the formula for calculating the area of
- a) an isosceles triangle
- b) an isosceles trapezoid
Solution:
a) Isosceles triangle
The isosceles triangle has a base a and height v. Let S1 be half of the area of this triangle, which is bounded by the x-axis, lines parallel to the y-axis at the points a = 0, b = v, and the line
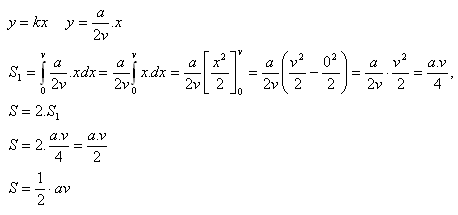
b) Isosceles trapezoid
The isosceles trapezoid has an upper base a, a lower base b, and height v. Let S1 be half of the area of this trapezoid, which is bounded by the x-axis, lines parallel to the y-axis at the points a = 0, b = v, and the line
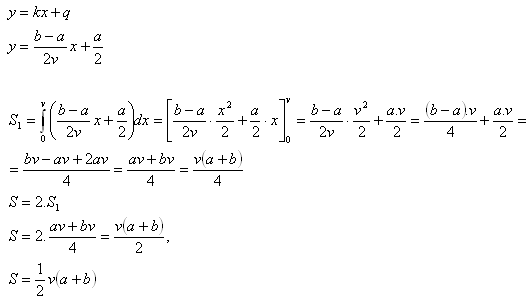
4.Calculate the area of the figure bounded by the parabola y = x2 + 1 and the line y = 5.
Solution:
The intersections of the line y1 = 5 and the parabola y2 = x2 + 1 are the limits of the integral.
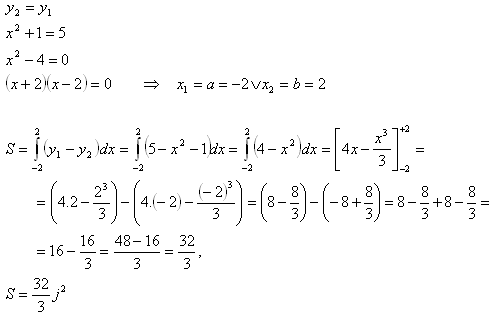
5.Using a definite integral, calculate the area of the plane figure bounded by the parabolas
y = 6 – 4x + x2 and y = –3 + 8x – 2x2.
Solution:
The intersections of the parabolas y1 = 6 – 4x + x2 and y2 = –3 + 8x – 2x2 are the limits of the integral.
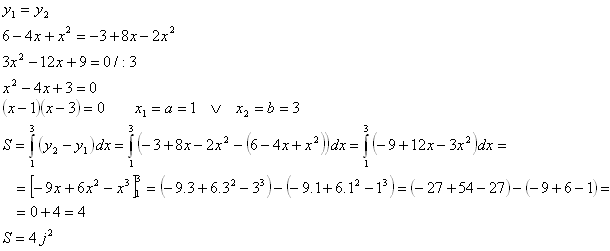
6. Derive the formula for calculating the area of a circle with radius r.
Solution:
First, let us prove that the equations x = r·cos t and y = r·sin t are parametric equations of a circle.
Proof:
x2 + y2 = r2
r2cos2t + r2sin2t = r2
r2(cos2t + sin2t) = r2
r2·1 = r2
r2 = r2 – the statement holds
S1 is one quarter of the circle, which is bounded by the x-axis, the y-axis (x = 0), and the circular arc y = r·sin t
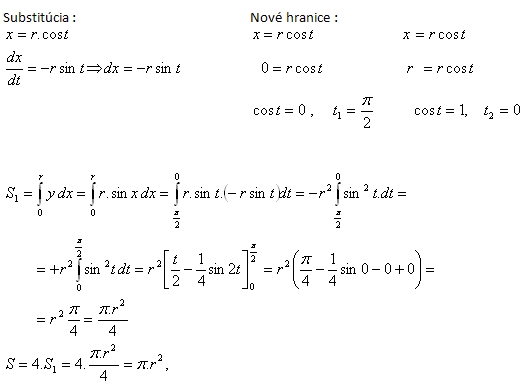
7.Derive the formula for the area of an ellipse with semi-axes “a” and “b”.
Solution:
First, let us prove that the equations x = a·cos t and y = b·sin t are parametric equations of an ellipse.
Proof: