sk|cz|de|

Physics

Acoustics

1.What is acoustics?

Solution:

Acoustics is the branch of physics that deals with physical phenomena involved in the transmission of sound. A source of sound is any body that can vibrate.

Sound:
a) Tone – a regular sinusoidal waveform (human vocal cords, strings, air columns, musical instruments)
b) Noise – an irregular waveform (banging, rustling, creaking)

Sound intensity:

I=PS=Wt⋅S,[I]=W m−2I=\frac{P}{S}=\frac{W}{t\cdot S},\qquad [I]=\mathrm{W\,m^{-2}}

Threshold of hearing I0=10−12 W m−2, threshold of pain Ib=10 W m−2

Sound intensity level:

L=10⋅log⁡ ⁣(II0),[L]=dB (decibel)L = 10 \cdot \log\!\left(\frac{I}{I_0}\right),\qquad [L]=\mathrm{dB}\ \text{(decibel)}

Pitch – determined by the frequency of vibration

fz=v2lf_z=\frac{v}{2l}

Timbre (tone color) – determined by the presence of higher harmonic frequencies

fk=k⋅v2lf_k = k\cdot \frac{v}{2l}

Speed of sound in air:

v=(331.8+0.61 t) m s−1v = (331.8 + 0.61\,t)\ \mathrm{m\,s^{-1}}

(where t tis temperature in °C)

String:

l=kλ2  (k=1,2,3,…),fz=v2ll = k\frac{\lambda}{2}\ \ (k=1,2,3,\ldots), \qquad f_z=\frac{v}{2l}

Open pipe:

l=kλ2  (k=1,2,3,…),fz=v2ll = k\frac{\lambda}{2}\ \ (k=1,2,3,\ldots), \qquad f_z=\frac{v}{2l}

Closed pipe:

l=kλ4  (k=1,3,5,…),fz=v4ll = k\frac{\lambda}{4}\ \ (k=1,3,5,\ldots), \qquad f_z=\frac{v}{4l

  

2.Calculate the speed of sound in air

  • a.) at temperature t = 0o C
  • b.) at temperature t = 15o C
  • c.) at what temperature is the speed of sound in air v = 351.32 m·s-1? The speed of sound in air as a function of ambient temperature is given by v = 331.8 + 0.61·t  (m·s-1).

Solution:

a.) t = 0oC, v0 = (331,8 + 0,61·0) m·s-1 = 331,8 m·s-1 => v0 = 331,8 m·s-1

b.) t = 15oC, v15 = (331,8 + 0,61·15oC) m·s-1 = 340 m·s-1 => v15 = 340 m·s-1

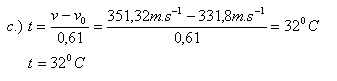
fyzika-akustika-2.gif 

The speeds of sound in air are v0 = 331,8 m·s-1, v15 = 340 m·s-1.

The speed of sound in air v = 351,32 m·s-1 is reached at temperature t = 32oC.

The speed of sound in air v15 = 340 m·s-1 is used when solving problems (unless stated otherwise).

3.Calculate the wavelengths corresponding to the limits of the audible frequency range 16 Hz – 20,000 Hz. v = 340 m·s-1.

Solution:

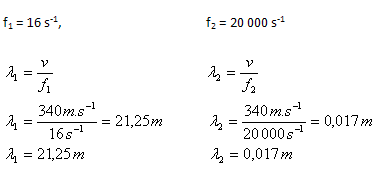
fyzika-akustika-3.gif 

The wavelengths corresponding to the limits of audibility are 0.017 m – 21.25 m.

4.Four sea ...

  • a.) On the sea surface there are two boats at a mutual distance of 11.6 km. The first sends a sound signal through the water and simultaneously a light signal above the water. The second boat receives both signals, the sound one 8 s later than the light. Determine the speed of sound in seawater.
  • b.) A sailor on a boat heard thunder 10 s after he saw the flash. At what distance did the lightning strike?
  • c.) Sound reflected from a pod of whales returned to the boat after 1 second. How far are the whales from the boat?
  • d.) On one boat the sea depth was measured with ultrasound. What is the depth there if the reflected ultrasonic signal returned to the boat after 0.8 s?

Solution:

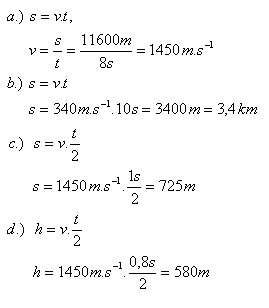
fyzika-akustika-4.gif

5.An observer standing at the edge of the Macocha Abyss dropped a stone into it and heard it hit the bottom after 5.6 s. Determine the depth of the abyss!

t1 – time of the stone’s fall,  t2 – time of sound propagation after the impact at the bottom

Solution:

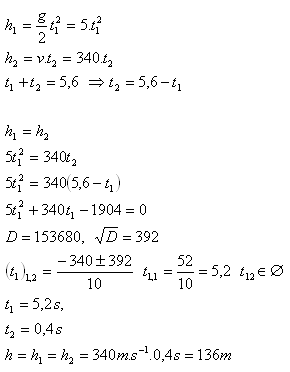
fyzika-akustika-5.gif 

The depth of the Macocha Abyss is about 136 m.

6.If we shorten the length of a string (with unchanged tension) by 10 cm, its fundamental frequency changes by a factor of 1.5. Determine the original length of the string l.

Solution:

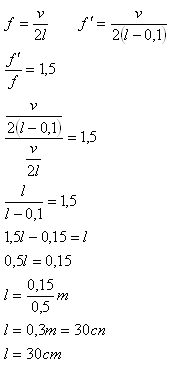
fyzika-akustika-6.gif 

The original length of the string was l = 30 cm.

7. What length must

  • a.) an open pipe have
  • b.) a closed pipe have
if they produce a tone with frequency f = 130.5 Hz at temperature t = –5oC?

Solution:

Analysis:

v = 331,8 + 0,61·t

v–5 = (331,8 + 0,61·(–5)) m·s-1 = 328,75 m·s-1 

a.) Open pipe:

f=v2lf = \frac{v}{2l}l=v2f=328.75 m⋅s−12⋅130.5 s−1=1.26 ml = \frac{v}{2f} = \frac{328.75\ \mathrm{m·s^{-1}}}{2 \cdot 130.5\ \mathrm{s^{-1}}} = 1.26\ \mathrm{m}

b.) Closed pipe:

f=v4lf = \frac{v}{4l}l=v4f=328.75 m⋅s−14⋅130.5 s−1=0.63 ml = \frac{v}{4f} = \frac{328.75\ \mathrm{m·s^{-1}}}{4 \cdot 130.5\ \mathrm{s^{-1}}} = 0.63\ \mathrm{m}

 

 The open pipe must be 1.26 m long, the closed one 0.63 m.

8.By how many decibels does the sound intensity level increase if the sound intensity increases 100,000 times? What will this increased intensity be?

Solution:

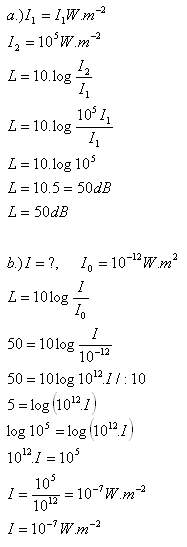
fyzika-akustika-8.gif 

The sound intensity level increases by 50 dB.

The increased sound intensity will be I = 10-7 W·m-2.

9.What is the Doppler principle (effect)?

Solution:

The Doppler principle explains the change in the observed frequency of sound waves caused by the relative motion of the sound source and the observer.

Let v – speed of sound, u – speed of the observer,

w – speed of the sound source, f – frequency emitted by the source,

f‘ – frequency perceived by the observer.

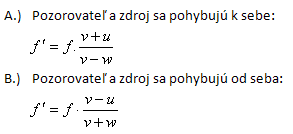
A.) The observer and the source are moving toward each other:

f′=fv+uv−wf' = f \frac{v + u}{v - w}

B.) The observer and the source are moving away from each other:

f′=fv−uv+wf' = f \frac{v - u}{v + w

Note: Johann Christian Doppler (1803 – 1853) Austrian mathematician and physicist. He worked in Vienna, Prague, and at the Mining Academy in Banská Štiavnica (1847).

10.
John is standing by a highway along which an ambulance is moving at speed w = 20 m·s-1. The siren of the ambulance emits a steady tone of frequency 1,000 Hz. What frequency does John register when the ambulance

  • a.) is approaching
  • b.) is receding. 
The air temperature is t = 20oC

Solution:

Analysis:

v = 331,8 + 0,61·20 = 344 m·s-1, w = 20 m·s-1, f = 1,000 Hz, u = 0

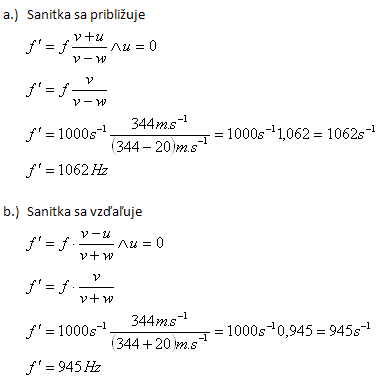
a.) The ambulance is approaching:

f′=fv+uv−w,and since u=0f' = f \frac{v + u}{v - w}, \quad \text{and since } u = 0f′=fvv−wf' = f \frac{v}{v - w}f′=1000 s−1344 ms−1(344−20) ms−1=1000 s−1×1.062=1062 s−1f' = 1000\,\text{s}^{-1} \frac{344\,\text{m·s}^{-1}}{(344 - 20)\,\text{m·s}^{-1}} = 1000\,\text{s}^{-1} \times 1.062 = 1062\,\text{s}^{-1} f′=1062 Hzf' = 1062\,\text{Hz}

b.) The ambulance is moving away:

f′=fv−uv+w,and since u=0f' = f \frac{v - u}{v + w}, \quad \text{and since } u = 0f′=fvv+wf' = f \frac{v}{v + w}f′=1000 s−1344 ms−1(344+20) ms−1=1000 s−1×0.945=945 s−1f' = 1000\,\text{s}^{-1} \frac{344\,\text{m·s}^{-1}}{(344 + 20)\,\text{m·s}^{-1}} = 1000\,\text{s}^{-1} \times 0.945 = 945\,\text{s}^{-1}f′=945 Hzf' = 945\,\text{Hz}

 


John registers a frequency of 1062 Hz in the first case and 945 Hz in the second.