Practical Problems
1.A triangle has a perimeter of 35 cm. One of it‘s sides is four times greater than the second one and 1 cm greater than the third one. Determine the size of it‘s sides.
Solution:
Analysis:
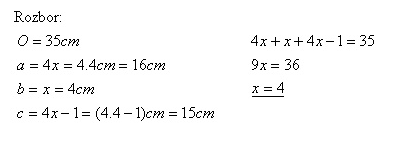
The sizes of the triangle‘s sides are: a = 16 cm, b = 4 cm a c = 15 cm
2.In the class there are 30 pupils. On the final exams nobody had worse grade than 2 (B). The average grade of the class in mathematics was 1.4. Determine the count of the pupils who had 1 (A) from the mathematics.
Solution:
Analysis:
Number of grade A students:
Number of grade B students:
In the class there are 18 pupils who had 1 (A) and 12 pupils who had 2 (B).
3.One quarter of the competitors were faster than John, two thirds of the competitors were slower than John. How many competitors were running?
Solution:
All competitors:
In front of John:
Behind John:
John:
There were 12 competitors.
4.There are 30 boys and an unknown number of girls in a class. All the girls and 28 boys, what translates to 95% of all the pupils, went to a ski trip. What is the percentage of girls in the class?
Solution:
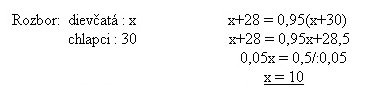
In the classroom there are 10 girls, 25% of 40 pupils.
5. 120 litres of vine are stored in 141 bottles. Some of them have volume of 1 litre, the other have volume of 0.7 litre. How many of each bottles were used?
Solution:
Analysis:
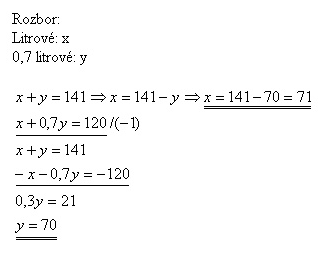
There are 71 1l bottles, and 70 0,7l bottles.
6.One bricklayer can build a wall in 30 hours. Each of the two apprentices can do in 40 hours. How many hours do they need to build the wall together?
Solution:
-
The master in 1 hour builds of the wall, in x hours of the wall.
-
The first apprentice in 1 hour builds of the wall, in x hours of the wall.
-
The second apprentice in 1 hour builds of the wall, in x hours of the wall.
Together in x hours they build one whole wall:
Together they can build the wall in 12 hours.
7. The perimeter of a rectangle is 82 m, the length of his diagonal is 29 m. Determine the sizes of the sides of the rectangle.
Solution:
Analysis:
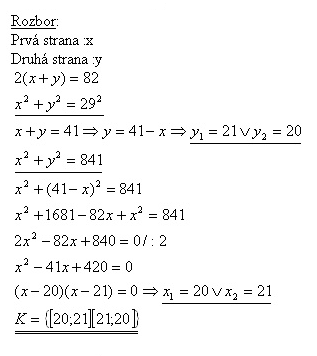
The sizes of the sides are 20 m and 21 m.
8.The perimeter of a right triangle is 84 cm, the hypotenuse is 37 cm long. Determine the lengths of the catheties.
Solution:
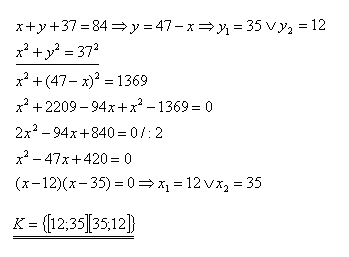
The catheties are 12 cm and 35 cm long.
9.Two resistors connected in line have final resistance of 18 Ω, parallely 4 Ω. Determine the resistance of each resistor.
Solution:
Analysis:
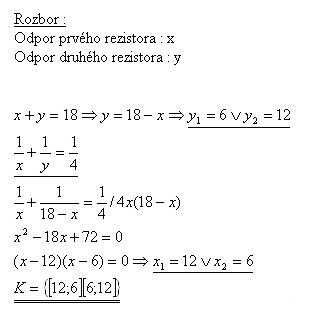
The resistances of the resistors are 12 Ω and 6 Ω.
10.The area of a right triangle is S = 180 m2, one of it‘s catheties is 31 m longer than another one. Determine lengths of the sides.
Solution:
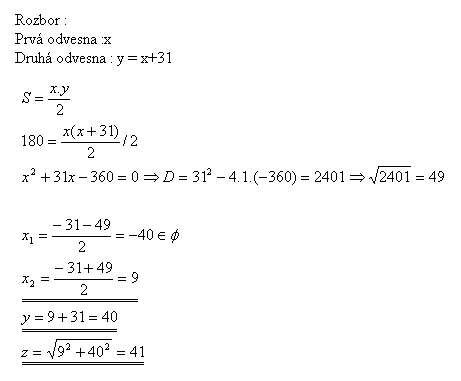
The catheties are 9 m and 40 m long, the hypotenuse is 41 m long.
11.The size of the resultant force of tho forces interacting in right angle is 25 N. If you amplify the weaker force by 8 N and lower the greater force by 8 N, the resultant power will remain unchanged. Determine both forces.
Solution:
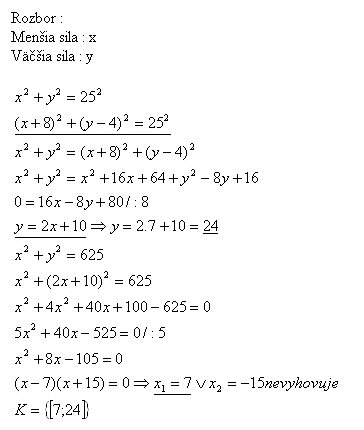
The forces are 7 N and 24 N.
12. Which x-gon has 54 diagonals?
Solution:
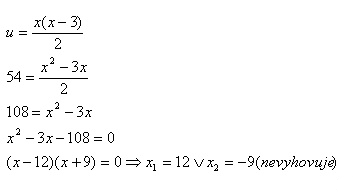
The 12-gon has 54 diagonals.
13.We‘d like to have a rectangular flowerbed of area 8 m2 on a rectangular area with sides 12 m and 10 m long, so that it‘s borders would have the same distance from the borders of the area. Determine the sides of the flowerbad.
Solution:

Sides of the flowerbed are 4 m and 2 m long.
14. Two polygons have 24 sides and 109 diagonals together. How many sides has each of them?
Solution:
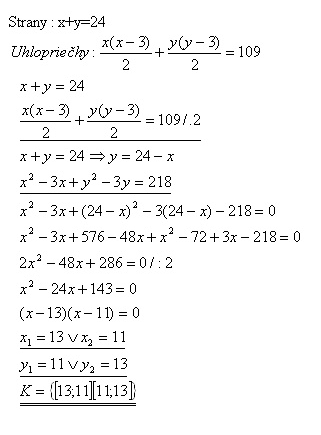
The polygons have 13 and 11 sides.
15.A right triangle has a hypotenuse 65 m long. The difference of lengths of the catheties is 23 m. Determine the perimeter of the triangle.
Solution:
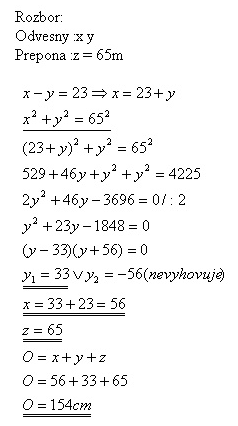
The perimeter of the triangle is 154 cm.
16.The distance between the centres of two tangent circles is 12 cm. Sum of their areas is 80 Pí cm2. Determine the radius of both circles.
Solution:
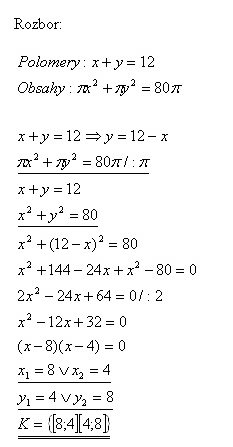
Radius of the first circle is 8 cm, radius of the second circle is 4 cm.
17.The stairway is 3,6 m high. If the number of stairs raised by 3, the height of one stair would lower by 4 cm. How many stairs are there?
Solution:
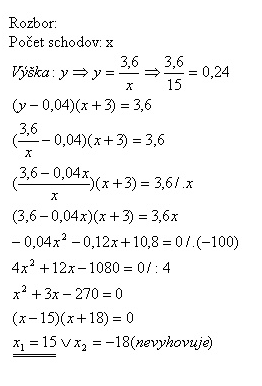
There are 15 stairs, each 0,24 m height.
18.If the 2 digits number is multiplied by the sum of it‘s digits, we gain 1666. Number of tens in the number is greater than the number of ones by 1. What‘s the number?
Solution:
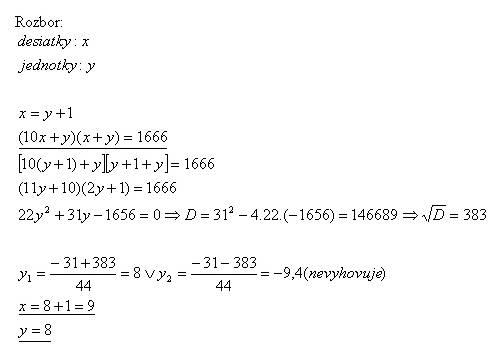
It‘s number 98.
19.The difference between the areas of two cubes is 19272 cm2. One cube‘s side is 22 cm longer than the other‘s. Determine length of sides of both the cubes.
Solution:
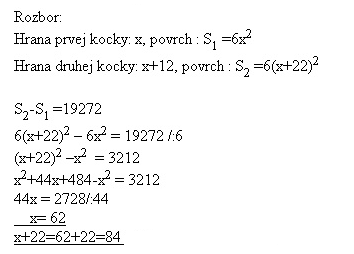
The lengths of sides are 62 cm and 84 cm.
20.The side of one cube is greater than the side of the second cube by 2 cm. The volume difference is 728 cm3. Determine lengths of the sides of both the cubes.
Solution:
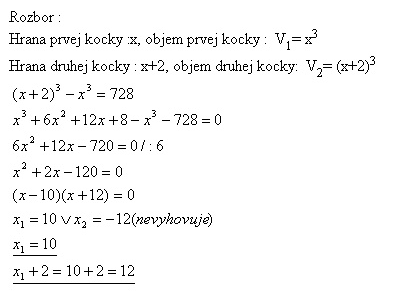
The length of the first cube‘s side is 10 cm, the length of the second cube‘s side is 12 cm.
21.In the cuboid-shaped water tower there is 1500 hl (150 m3) of water. The height of the water level is 2.5 m. One side of the bottom is 4 m greater than the other one. Determine the dimensions of the bottom rectangle.
Solution:
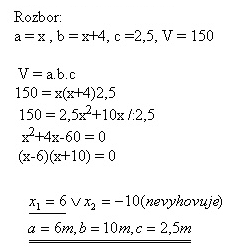
Bottom dimensions are 6 m and 10 m.
22.A cilinder‘s radius is 2 cm shorter than it‘s height, it‘s area is 704 cm2. Determine the volume of the cylinder.
Solution:
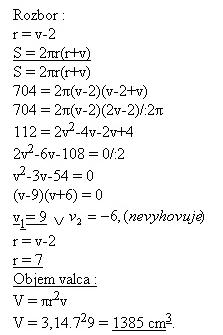
The volume of the cilinder is 1385 cm3.
23.A diamond has a perimeter of 104 cm, area of 480 cm2. Determine the lengths of the diagonals.
Solution:
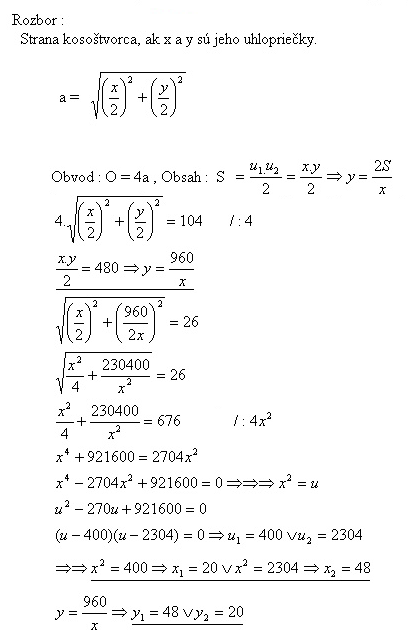
The lengths of the diagonals are 20 cm and 48 cm.