Radioactivity
1. What is radioactivity?
Solution:
Radioactivity is the transformation (decay) of atomic nuclei. The nucleus of one element gradually changes into the stable nucleus of another element, while energy is emitted. Natural radioactivity (M. Becquerel and P. Curie) is the spontaneous decay of unstable nuclei. Artificial radioactivity (I. and F. Joliot Curie) arises from artificially prepared nuclear reactions.

2.Determine the sequence of radioactive transformations in the thorium decay series.
Solution:
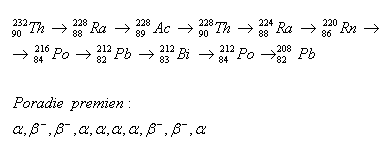
3. Determine the composition of the nucleus of the isotope of the element that arises from uranium.
Solution:
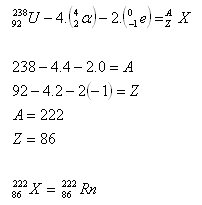
The element sought is an isotope of radon. [Determined using tables].
4.Complete the nuclear reaction equations:
Solution:
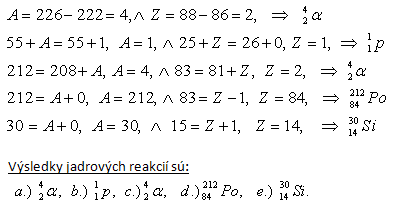
5.Determine the half-life of uranium if its decay constant is λ = 4.33·10-4 year-1.
Solution:
Analysis:
λ = 4.33·10-4 year-1
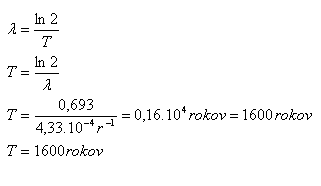
After 1600 years, exactly half of the uranium nuclei will have decayed.
6.A nuclide has a half-life of 2400 seconds. What percentage of nuclei decay in 300 seconds?
Solution:
Analysis:
T = 2400s, t = 300s, ln2 = 0.693, e = 2.718282, N = ?, N‘ = ?
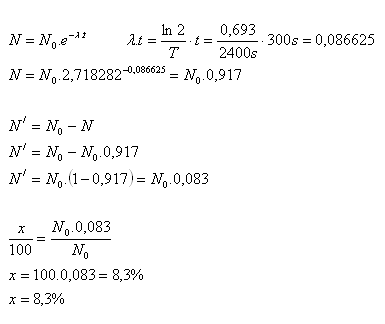
In 300 seconds, 8.3% of the nuclei decay.
7.The number of decays in 1 gram of radium is 3.7·1010s-1. Determine the half-life.
Solution:
Analysis:
m = 1g = 10–3kg, N‘ = 3.7·1010s-1, A = 226, mu = 1.6605·10–27kg, T = ?, 1 year = 3.15·107s
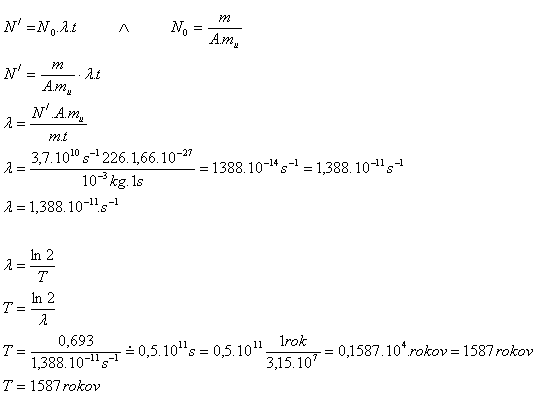
The half-life of radium is about 1587 years.
8.After what time will half of the nuclei of a radionuclide decay if its decay constant is λ = 1.42·10–11s-1?
Solution:
Analysis:
λ = 1.42·10–11s-1, 1 year = 3.1536·107s, ln e = 1, ln 0.5 = –0.693, t = ?
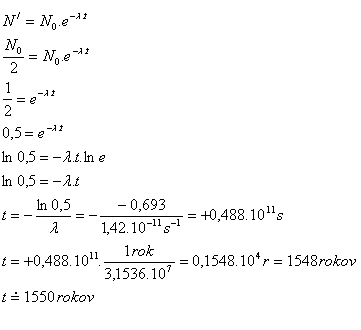
Half of the radionuclide nuclei will decay in about 1550 years.
9.When determining the age of the burial boat from the tomb of Sesostris III, it was found that the concentration of carbon in the wood from which the boat was made is approximately N = 0.645·N0. N0 is the concentration of carbon in present-day living organisms. Determine the age of the burial boat if the half-life of carbon is 5730 years.
Solution:
Analysis:
N = 0.645·N0, T = 5730 years, ln2 = 0.693, t = ?
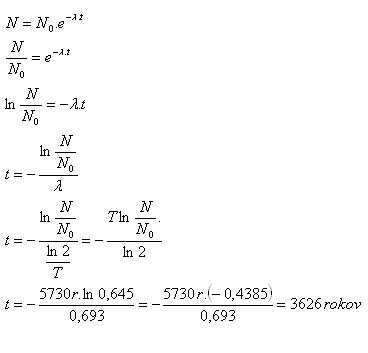
Sesostris III was buried 3626 years ago.
The so-called “carbon method” was used to determine the age of archaeological objects.
10.In September 1991, tourists discovered in the Ötztal Alps in Austria an ice-mummified human body. Using the carbon method, it was found that for the undecayed nuclei in his body N and the nuclei in the bodies of present-day people N it holds that N = 0.5268·N0. How many years ago did this man freeze, if the half-life of carbon is T = 5730 years?
Solution:
Analysis:
N = 0.5268·N0, T = 5730 years, ln2 = 0.693
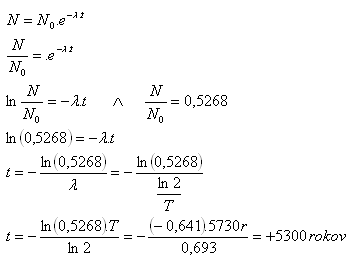
The man in the Alps froze about 5300 years ago.