Quadratic Equation by Discussion
1. Use the discriminant to find out the count of the roots of following equations:
| x2–14x +33=0 |
D=(-14)2-4.1.33=64 |
Two different roots in real numbers |
| 4x2–5x+1=0 |
D=(-5)2-4.4.1=9 |
Two different roots in real numbers |
| x2–10x+25=0 |
D=(-10)2-4.1.25=0 |
One (double) root in real numbers |
| 12x2–5x-3=0 |
D=(-5)2-4.12.(-3)=169 |
Two different roots in real numbers |
| x2–4x+13=0 |
D=(-4)2-4.1.13=–36 |
No solution in real numbers |
| x2–14x+49=0 |
D=(-14)2–4.1.49=0 |
One (double) root in real numbers |
| x2–6x+25=0 |
D=(-6)2-4.1.25=–64 |
No solution in real numbers |
2. For which „m“ do the quadratic equations have one (double) real root?
a.) x2+4x+m = 0
D = 0
b2-4ac = 0
42-4.1.m = 0
4m = 16
m = 4
x2+4x+4=0
b.) mx2+(4m-2)x+(4m+1) = 0
D = 0
b2–4ac = 0
(4m-2)2–4m(4m+1) = 0
16m2–16m+4–16m2–4m = 0
–20m = –4
m = 1/5
x2-6x+9 = 0
c.) mx2+(2m–2)x+(m+2) = 0
D = 0
b2–4ac = 0
(2m-2)2–4m(m+2) = 0
4m2-8m+4–4m2-8m = 0
–16m = –4
m = ¼
x2–6x+9 = 0
3. For which „k“ does the equation kx2+(2k+1)x+(k-1)=0 have two different roots in real numbers?
D > 0
b2–4ac > 0
(2k+1)2-4k(k-1) > 0
4k2+4k+1–4k2+4k > 0
8k > -1
k > –1/8
4. Find „k“ so that the equation x2 -5x +k = 0 wouldn‘t have a root in real numbers.
5. Find „m“ so that the equation mx2 +2x +m = 0 would have 2 roots in real numbers!
6. Find all „a“, for which one of the equation‘s roots equals null. 2(a-1)x2–(2a-4)x+2a(a-3) = 0. Find out the second root.
7. For which „m“ does the following equation have 1 (double) root in real numbers?
8.
For which „m“ does the equation mx2 +(4m –2)x +(4m+1) = 0 have one (double) root in real numbers?
Solution:
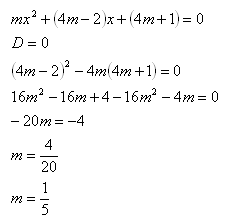
The equation has one (double) root in real numbers if and only if m = 1/5.
9.
For which parameters „a“ the equation‘s roots x2 – (3a+2)x + a2 = 0 fit the relation x1 = 9x2 ? Determine those roots!
Solution:
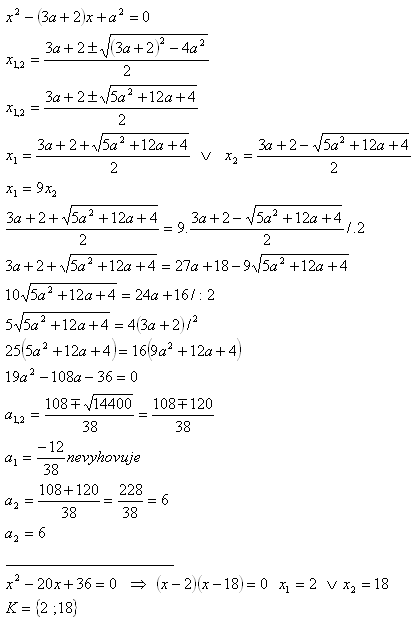
10.
For which parameters „a“ in equation 2x2 – (a+1)x+(a-1) = 0 fits x1 – x2 = x1 . x2 ?
Solution:
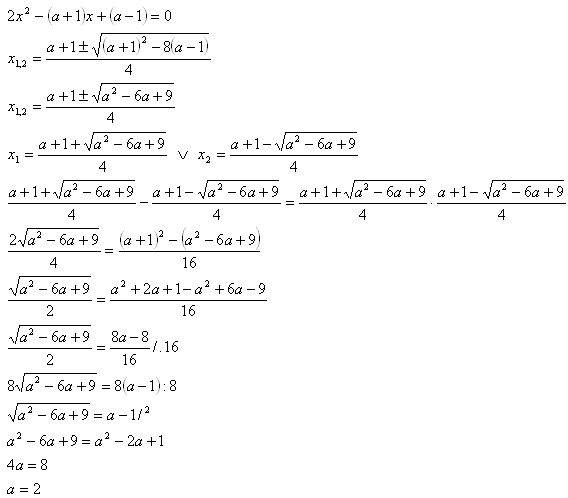
The parameter is a = 2, the equation is 2x2 – 3x+1 = 0.