Triangle
1.Characterize a triangle
Solution:

2.Prove for the exterior angles of a triangle: α*+ β*+ γ* = 360°.
Proof:
α + α* = 180°
β + β* = 180°
γ + γ* = 180°
_____________
α + β + γ + α* + β* + γ* = 540°
α* + β* + γ* = 540° – (α + β + γ)
α* + β* + γ* = 540° - 180°
α* + β* + γ* = 360°
3. A triangles‘ side size c = 10 cm. For it‘s angles stands: α:β:γ = 3:5:10.
Determine:
a) perimeter
b) area
Solution:
Perimeter
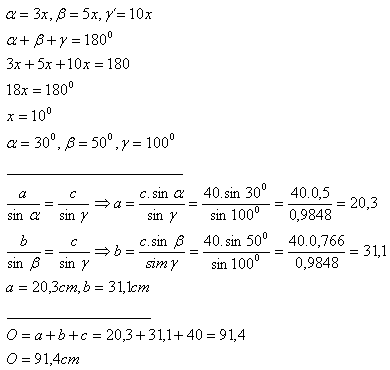
Area
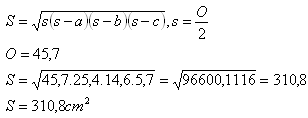
4.An equilateral triangle‘s side length a = 10 cm.
Determine the size of the area between the circumcircle and the incircle.
Solution:
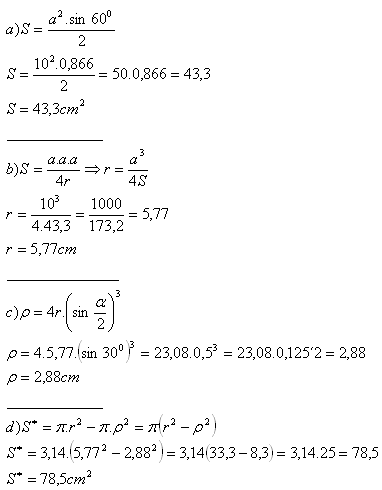
5.John stands 5 m and 8 m from the edges of a tree. He can see the tree under the angle of 60°.
Determine the length of the tree.
Solution:
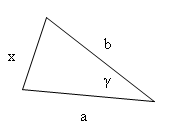
a = 5 m
b = 8 m
γ = 60°
x
2 = a
2 + b
2 -2ab.cosγ
x
2 = 5
2 + 8
2 -2.5.8.cos60°
x
2 = 25 + 64 – 80.0,5
x
2 = 25 + 64 – 40
x
2 = 49
x = 7
The tree is 7 m long.
6.There are three tangent circles with radius r1 = 2 cm, r2 = 3cm, r3 = 4cm. Centres of the circles define a triangle.
Determine the inner angles of the triangle.
Solution:
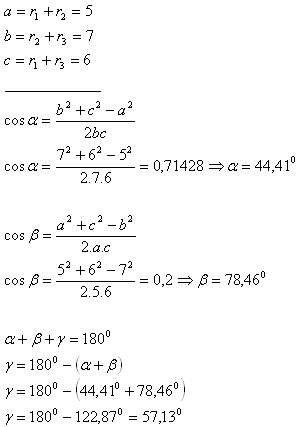
Inner angles of the triangle equal α = 44,41°, β = 78,46° and γ = 57,13°.
7.Two trains left a train station in the same time on two tracs forming the angle φ = 156°. Their speeds are v1 = 13 ms-1, v2 = 14,5 ms-1.
Determine their distance in the time t = 5 min.
Solution:
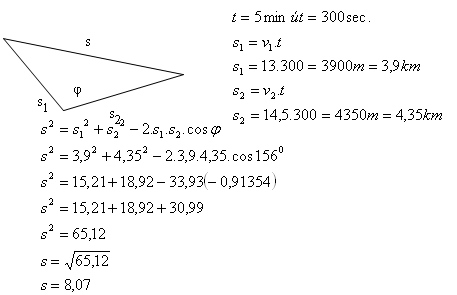
The distance between the trains after 5 minutes is 8.07 km.
8. Forces F1, F2 act from the same point of application. Angle between the forces φ = 60°.
Determine the size of the resultant power, if F1 = 42N, F2 = 35N.
Determine the angles between the forces F1, F2 and the resultant power.
Solution:
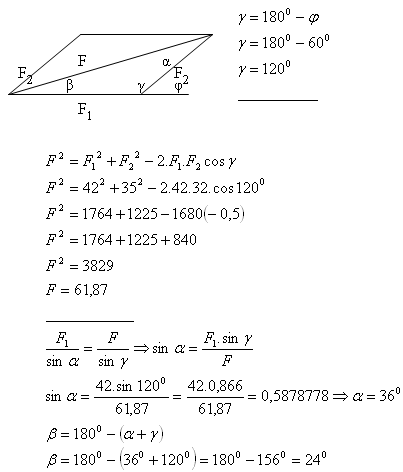
The resultant power F = 61,87N.
The angles are α = 36° and β = 24°.
9.The angle between the coasts of a river observed from a 20 m height tower which is 20 m far from the river is 15°.
Determine the width of the river.
Solution:
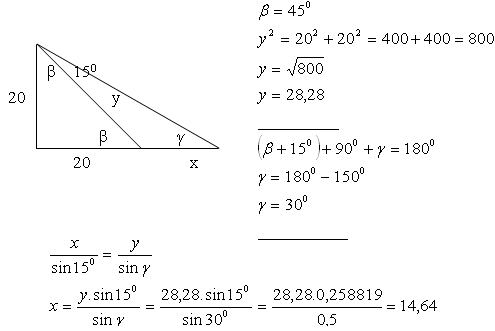
The width of the river is x = 14,64 m.
10. An object of weight m = 1563 kg hangs on a horizontal girder. It‘s fastened by two ropes of different length. The angles between a ropes and the girder equal α = 48°, β = 62°.
Determine the forces acting on the ropes. (F = 15630 N)
Solution:
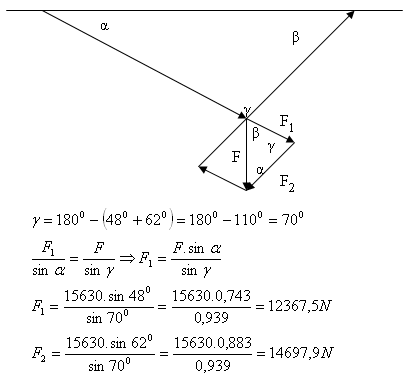
The forces acting on the ropes are F
1 = 12367,5 N and F
2 = 14697,9 N.