sk|cz|

Physics

Reflection and refraction

1.What happens when light passes through the interface of two media?

Solution:

When light passes through the interface of two media from the first medium (where it moves with velocity v1) into the second medium (where it moves with velocity v2), two cases may occur:

  • reflection of light
  • refraction of light

Reflection of Light:

Reflection of light occurs when light strikes a medium into which it cannot penetrate.

Law of Reflection:
α=α′\alpha = \alpha'
The angle of reflection α′\alpha' equals the angle of incidence α\alpha. The reflected ray lies in the plane of incidence.

Total Internal Reflection – refraction of light from an optically denser medium into an optically less dense medium. (β=90∘\beta = 90^\circ)

sin⁡αm=1n1,n2=1,αm=critical angle\sin \alpha_m = \frac{1}{n_1}, \quad n_2 = 1, \quad \alpha_m = \text{critical angle}

Refraction of Light:

Refraction of light occurs when light passes into another medium.

Law of Refraction (Snell’s Law):

sin⁡αsin⁡β=v1v2=n2n1\frac{\sin \alpha}{\sin \beta} = \frac{v_1}{v_2} = \frac{n_2}{n_1}

  • α\alpha = angle of incidence,

  • β\beta = angle of refraction,

  • n1n_1 = refractive index of the first medium,

  • n2n_2 = refractive index of the second medium.

If β<α\beta < \alpha, the ray bends toward the normal.
If β>α\beta > \alpha, the ray bends away from the normal.

Absolute Refractive Index:

n=cv=cλf=λ0λn = \frac{c}{v} = \frac{c}{\lambda f} = \frac{\lambda_0}{\lambda}

Medium Air Water Ice Glass
nn 1.00 1.33 1.31 1.51

2.The speed of red light in glass is v1 = 199,200 km.s-1 and violet is v2 = 196,700 km.s-1. Determine the refractive index for red and violet light. (c = 3.108 m.s-1)

Solution:

Analysis:

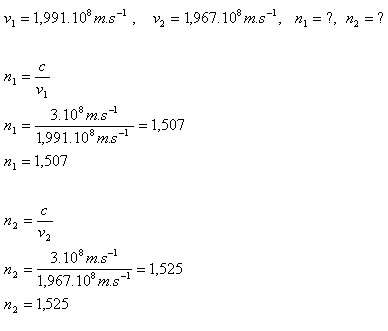
physics-reflection-and-refraction-2.gif 

The refractive index for red light in glass is n1 = 1.507, for violet light it is n2 = 1.525.

3.Light falls from air (n1 = 1) onto the wall of a diamond at an angle α = 680. The refracted ray is perpendicular to the reflected ray. Calculate:

  • the refractive index of the diamond for the used light
  • the speed of light in the diamond (c = 3.108 m.s-1)

Solution:

Analysis:

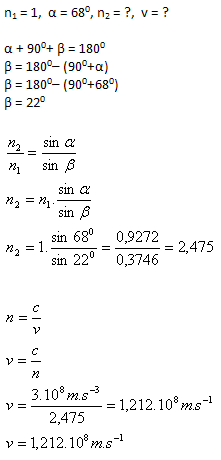
physics-reflection-and-refraction-3.gif 

  • The refractive index of diamond is n2 = 2.475.
  • The speed of light in diamond is v = 1.212·108 m.s-1.

4.Light falling from air onto the surface of water (n = 1.33) is refracted at an angle β = 300. Determine the angle of incidence α and the angle of reflection α‘.

Solution:

Analysis:

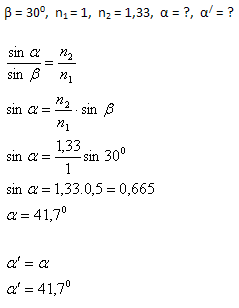
physics-reflection-and-refraction-4.gif 

The angle of incidence is α = 41.70, the angle of reflection is α‘ = 41.70.

5.At the bottom of a lake, a vertical post 1 meter long is planted so that it is completely submerged under the water surface. Determine the length of its shadow on the bottom of the lake if n1(air) = 1, n2(water) = 1.33, and the Sun is φ = 300 above the surface.

Solution:

Analysis:

l = 1m, n1(air) = 1, n2(water) = 1.33, φ = 300, t = ? α = 900– φ = 900 – 300 = 600

The post “l” and the shadow “t” form a right triangle. The angle β is the opposite angle of side “t” in this triangle.


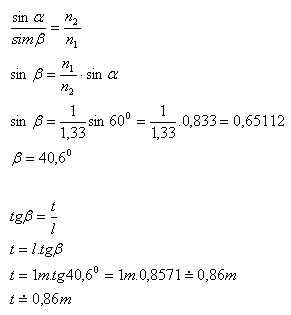
 physics-reflection-and-refraction-5.gif

The length of the shadow of the post is 0.86m.

6.A light ray falls from air onto a flat interface of air and glass, reflects at an angle of 600 and at the same time refracts into glass at an angle of 300. Determine the speed of light in glass.

Solution:

Analysis:

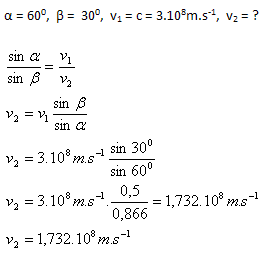
 physics-reflection-and-refraction-6.gif

The speed of light in glass is 1.732·108 m.s–1.

7.

The wavelength of yellow light in air is λ0 = 590 nm. What will be the wavelength of light in glass if n = 1.5? Also calculate the speed of light in this medium.

Solution:

Analysis:

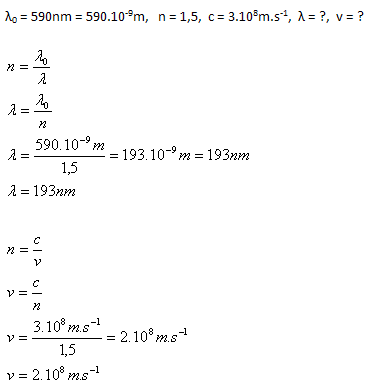
 physics-reflection-and-refraction-7.gif

The wavelength of yellow light in glass is λ = 163 nm, speed v = 2·108 m.s-1.

8.At what critical angle must light fall in order for total reflection to occur, if light passes:

  • a) from glass to air (n1 = 1.5)
  • b) from water to air (n‘1 = 1.33)
  • c) from glass to water n2(air) = 1

Solution:

Analysis:

physics-reflection-and-refraction-8.gif

The critical angles are approximately 41050‘, 48049‘, and 62027‘.

9. Determine the thickness of the soap bubble wall (n = 1.33) if white light falls on it. The first-order interference maximum is observed in green light (fZ = 5.7·1014 Hz).

Solution:

Analysis:

n = 1.33, fZ = 5.7·1014 Hz, c = 3·102 m.s-1, d = ? k = 1

This is an application of the relation for the first-order interference maximum by reflection.

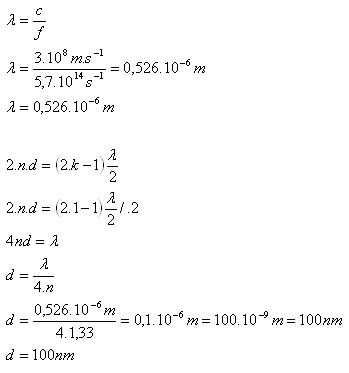
physics-reflection-and-refraction-9.gif 

The thickness of the soap bubble wall is d = 100 nm.

10.At the bottom of a stream 32 cm deep lies a pebble. A boy wants to touch it with a stick that he holds above the surface at an angle of 450. At what distance from the pebble will the stick touch the bottom of the stream after immersion? (n1=1, n2=1.33)

Solution:

Analysis:

pr-10 

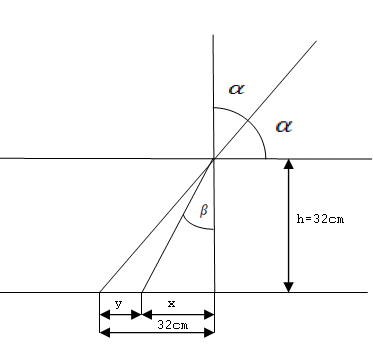
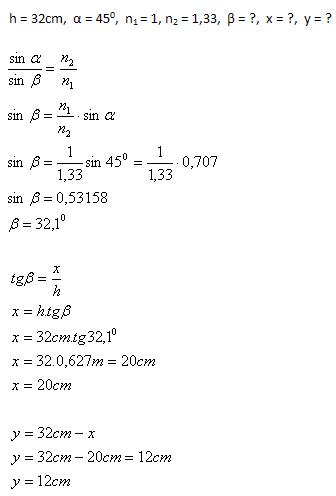
physics-reflection-and-refraction-10 

The stick will touch the bottom of the stream at a distance of 12 cm from the pebble.