Logarithms - Basics
Logarithm
Logarithm of a positive number x to the base a ( a is a positive number not equal to 1 ) is the power y to which the base a must be raised in order to produce the number x.
logax =y because ay=x a > 0 and a ≠ 1
Logarithms properties:
a.) logarithm of a product:
b.) logarithm of a quotient:
c.) logarithm of a power:
1. Rewrite to logarithm notation:
10
2 = 100 log
10 100 = 2
4
5 =1024 log
41024 = 5
13
0 = 1 log
131 = 0
10
-3 = 0,001 log
100,001 =-3
64
0,5 =8 log
648 = 0,5
5
-2 = 0,04 log
50,04=-2
2. Solve and give a reason:
log
101000 log
101000 = 3 because 10
3 = 1000
log
381 log
381 = 4 because 3
4 = 81
log
20,5 log
20,5 =-1 because 2
-1 = 0,5
log
171 log
171 = 0 because 17
0 =1
log
1111 log
1111 = 1 because 11
1 = 11
log
50,2 log
50,2 = -1 because5
-1 = 0,2
log
150 log
150 =
log
5(-25) log
5(-25) = n0
log
0,40,4 log
0,40,4 = 1 because 0,4
1 =0,4
log
149 log
149 = 0 undefined
3. Determine x:
log
2x = 3 x = 2
3 =8
log
10x = -4 x = 10
-4 = 0,0001
log
16x = 0,5 x =16
0,5= 4
log
20x =1 x = 20
1=20
log
25x = -0,5 x =25
-0,5 = 0,2
log
0.2487x = 0 x =0,2487
0 =1
4. Determine a:
loga25 =2 a = 5
loga81 = 4 a = 3
loga100000 =5 a = 10
loga512 = 3 a = 8
loga0,01 = -2 a = 10
loga5 = 0,5 a = 25
loga36 = 2 a = 6
loga64 = 1 a = 64
5. Logarithmize following expressions (to the base a)
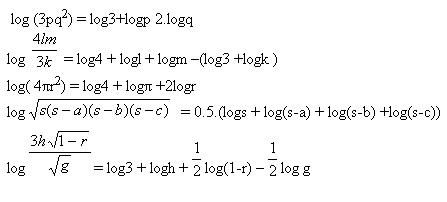
6. Determine x:
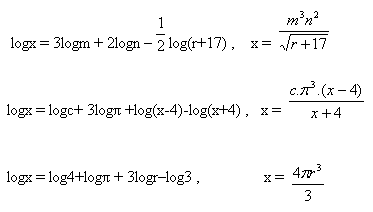
7. Enumerate the expression:
Solution:
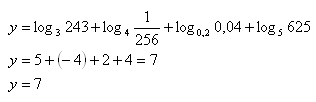
Reason:
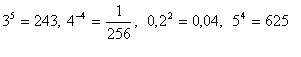
8. Logarithmize the expression (to the base a):
Solution:

9. Enumerate the expression:
Solution:
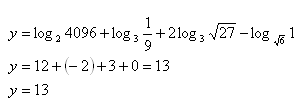
Reason:
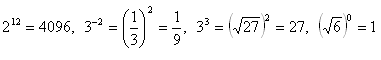
10. Enumerate the expression:
Solution:
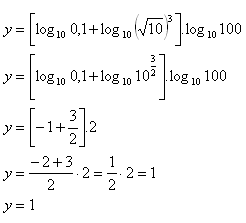
Reason:
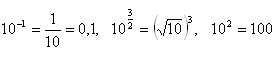
11. Use the decadic logarithm to solve the equation:
Solution:
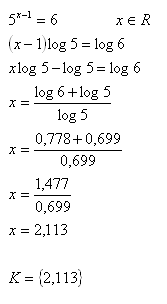
12.Use the decadic logarithm to solve the equation:
Solution:
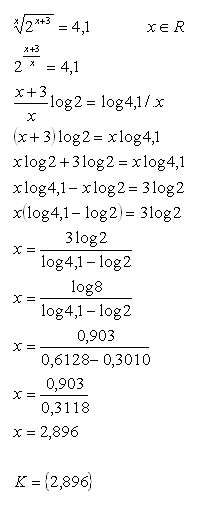
13.Use the decadic logarithm to solve the equation:
Solution:
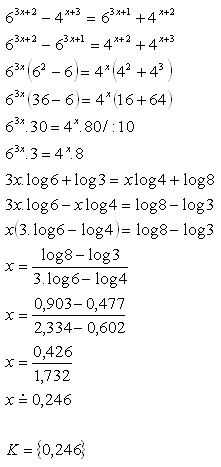
14.During t = 50 hours the activity of radioactive sodium lowers to 1/10 of the initial value. Determine the half life of the nuclide using a natural logarithm.
Solution:

Half life of a sodium nuclide equals T = 15 hours.