Density
1.Calculate the density of nitrogen in g.dm-3 under normal conditions.
Solution:
We substitute the values from the task and from tables into the equation for calculating density from the state equation.
Ar (N)=14.01
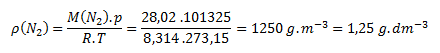
The density of nitrogen N2 under normal conditions is 1.25 g.dm-3.
2.Calculate the density of mercury in g.cm-3 at 20°C, if the molar volume of mercury at this temperature is 0.0148 dm3.mol-1.
Solution:
From tables we find M(Hg) = 200.59 g.mol-1. Substitute the values into the formula:
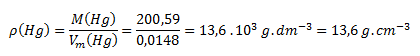
The density of mercury at 20°C is 13.6 g.cm-3.
3.Determine the molar mass of a gas that has a density of 1.429 kg.m-3 under normal conditions.
Solution:
From the density we can logically infer that 1000 liters of gas has a mass of 1.429 kg. Under normal conditions 1 mol of gas occupies 22.41 liters.
1000 l of gas.......................1.429 kg
22.41 l of gas......................x kg
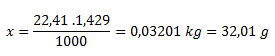
The molar mass of the unknown gas is 32.01 g.mol-1. From tables we see that it is oxygen.
4.It was measured that the density of an unknown gaseous saturated hydrocarbon is 21.88 times higher than the density of hydrogen under the same experimental conditions (pressure and temperature). Calculate the molar mass of the hydrocarbon and identify it using tables.
Solution:
For the density of gaseous hydrocarbon CxHy and hydrogen the following relations hold:
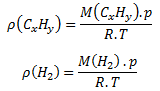
By dividing these two equations we obtain:
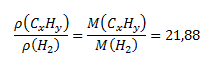
From this:
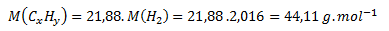
The molar mass of the unknown gaseous hydrocarbon is 44.11 g.mol-1. This corresponds to three carbons and eight hydrogens, i.e. propane C3H8.
5.Calculate the density in kg.m-3
- a) oxygen O2 under normal conditions
- b) ozone O3 under normal conditions
Solution:
a) Values from tables M(O2)= 31.998 g.mol-1 are substituted into the formula:
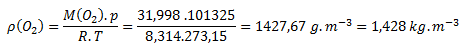
The density of oxygen under normal conditions is 1.428 kg.m-3.
b) Similarly for ozone, M(O3) = 47.997 g.mol-1
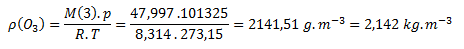
The density of ozone under normal conditions is 2.142 kg.m-3.
6.1 m3 of nitrogen has a mass of 1.25 kg under normal conditions. At what temperature and constant pressure will the density of nitrogen be halved?
Solution:
For the initial state of the gas:
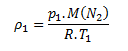
In the final state the density is:
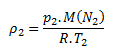
Since p1=p2, for the ratio of the two densities we have:
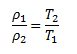
From this:
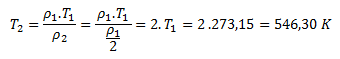
The density of the gas will be halved at a temperature of 546.3 K, i.e. 273.15 °C.
7.Calculate the relative molecular mass of a gaseous substance whose relative density compared to air is 1.586.
Solution:
The relative density of a gas is given by the relation:
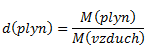
From this the molar mass of the gas:
M(gas)=d(gas).M(air)=1.586 .28.950=45.915 g.mol-1
The relative molecular mass of the gaseous substance is 45.915.
8.What is the relative density of natural gas compared to air, if this gas contains 75 vol.% CH4, 15 vol.% C2H4, 7 vol.% H2, 1 vol.% CO and 2 vol.% CO2.
Solution:
To calculate relative density we must calculate the molar mass of the gas:
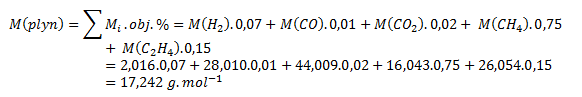
Relative density of natural gas:
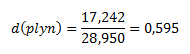
The relative density of natural gas compared to air is 0.595.
9.1 m3 of oxygen has a mass of 1.43 kg at 0°C and a pressure of 101.325 kPa. Calculate the density of oxygen at 23°C and a pressure of 95.99 kPa.
Solution:
We substitute the values from the task together with the molar mass of oxygen M(O2) = 31.998 g.mol-1 into the formula:
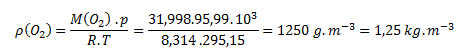
The density of oxygen under the given conditions is 1.25 kg.m-3.
10.1 m3 of gas has a mass of 1.33 kg at 100 kPa and 17°C. What will be the mass of 500 ml of the gas at 85.33 kPa and 37°C?
Solution:
First we need to determine the molar mass of the gas from the known data of the first system at 17°C.
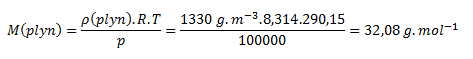
We rearrange the equation for calculating density from the state equation into the form:
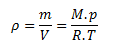
From which we calculate the mass:
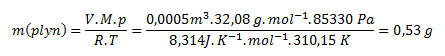
The mass of the gas under the given conditions is 0.53 g.