Golden ratio and Fibonacci

To divide a line segment in the golden ratio means to divide it in the ratio 1 : 0.618. The number τ is called the “golden number.” It is an irrational number. Calculated to eight decimal places, τ = 0.61803398..... This number has two interesting properties:

First property:

 

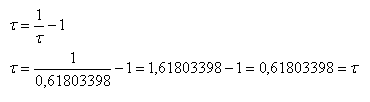
Second property:

The Italian mathematician Fibonacci (1170 – 1250) created a sequence of natural numbers named after him. The Fibonacci sequence is a sequence of natural numbers in which each subsequent term (except the first two) equals the sum of the two immediately preceding terms.

1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 989, ............. n

The ratio of two consecutive terms of the Fibonacci sequence approaches τ as n increases.

 

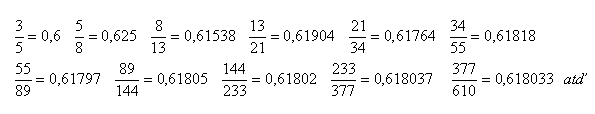
Interesting!

---