Line in a plane
1. Explain the different types of line equations in a plane.
- parametric form
- general form
- slope-intercept form
- distance from a point to a line
Solution:

2. Write the equation of the line passing through points A[2;7] and B[5;1] in the form:
a) parametric
b) general
c) slope-intercept
Solution:
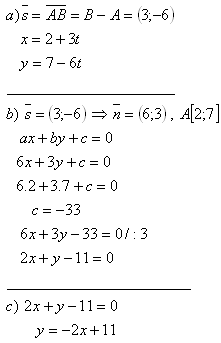
3. Write the equation of the line on which the midpoint of segment AB lies, if A[1;5] and B[7;3].
Solution:
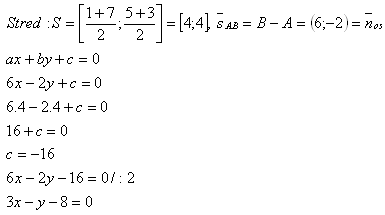
4. Write the equation of the line on which the altitude vc lies in triangle A[5;6], B[-2;4], and C[6;-1].
Solution:
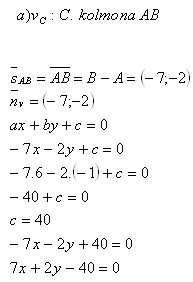
5. The line (2–m)x + 3my + (2m-6) = 0 is given.
Determine m so that:
a) the line passes through the origin
b) the line is parallel to the x-axis
c) the line is parallel to the y-axis
Solution:
a)
c = 0
2m – 6 = 0
m = 3
(2–3)x + 3·3y = 0
-x + 9y = 0
x – 9y =0
b)
a = 0
2 – m = 0
m = 2
3·2y + 2·2 – 6 =0
6y -2 = 0/:2
3y – 1 =0
c)
b = 0
2m = 0
m = 0
(2-0)x +(2·0 – 6) = 0
2x – 6 = 0/:2
x – 3 = 0
6. The line is given by p: 4x – 3y +6 = 0
a) find which of the points A[0;2] and B[-3;5] lies on the line
b) convert it to parametric form
c) calculate the distance from the point not on the line to the line
Solution:
a) A[0;2] lies on line p because:
4x -3y +6 = 0
4·0 -3·2 +6 = 0
0 = 0
Point B[-3;5] does not lie on line p because:
4x -3y + 6 =0
4·(-3) -3·5 +6 = -21
–21 ≠ 0
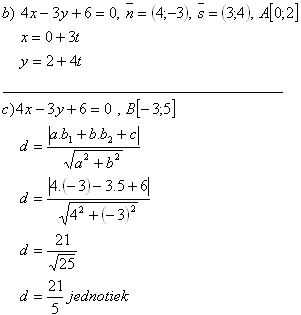
7. Write the equation of a line parallel to line p: 5x +12y -1 = 0 and at a distance d = 5 units from it.
Solution:
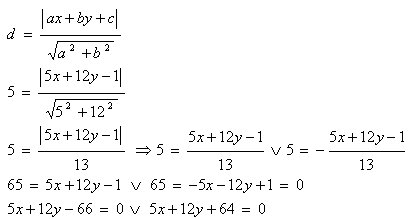
The required line equations are q1: 5x + 12y - 66 = 0 and q2: 5x + 12y + 64 = 0
8. The triangle has vertices A[-1;-5], B[9;-1], and C[1;7].
Write:
a) equation of side c = AB
b) equation of median tc
c) equation of altitude to side c, vc
Solution:
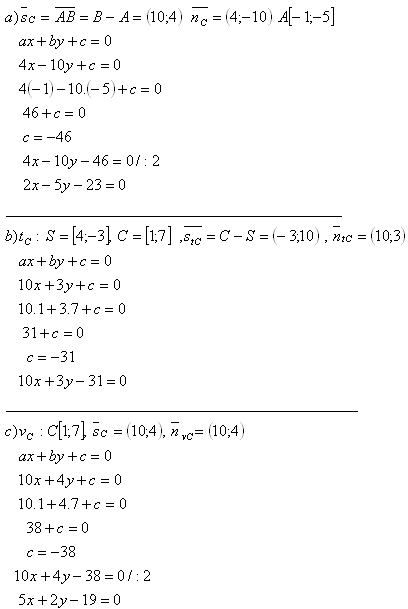
9. Write the equation of the line that makes an angle φ = 135° with the x-axis and passes through point A[3;-1].
Determine the segment the line cuts on the y-axis.
Solution:
A[3;-1]
φ = 135° = 3π/4
Slope k = tanφ = -1
y = kx + q
-1 = -1·3 + q
q = 2
y = -x + 2
10. A light beam originates from source A[-1;-5], reflects on the x-axis like from a mirror, and passes through point B[9;-5].
Write the equations of the incident and reflected beams.
Solution:

Equation for the incident beam: x – y – 4 = 0
Equation for the reflected beam: x + y – 4 = 0
11. The vertices of a triangle A and B and the intersection of the altitudes Q are given. Determine the coordinates of the triangle's vertex C if
Solution:
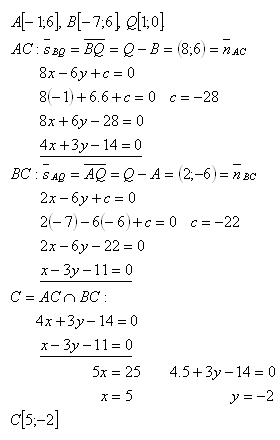
Vertex C has coordinates C [5;-2].
12. On line p, find point C, which is equidistant from points A and B.
Solution:
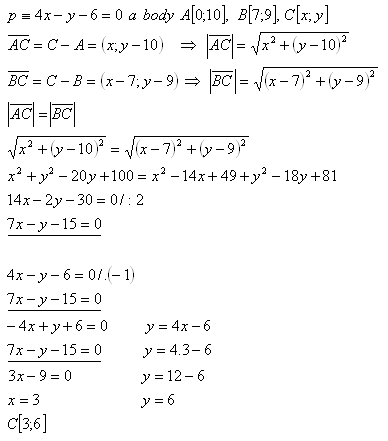
Point C[3;6] lies on line p.
13. Calculate the length of altitude va in triangle ABC if its sides have the equations
Solution:
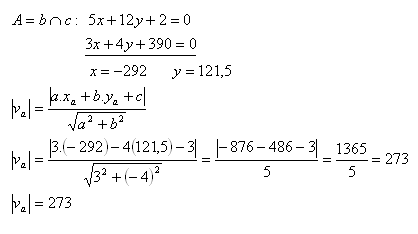
14. Opposite sides of square ABCD lie on parallel lines
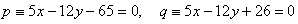
Calculate the perimeter and area of this square.
Solution:
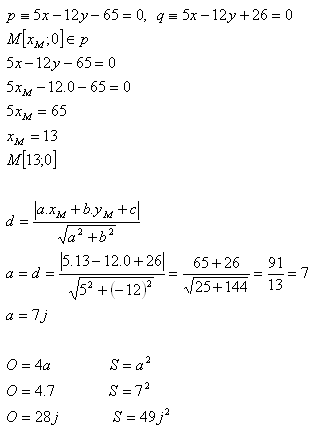
The perimeter of square ABCD is 28 units, its area is 49 units2.
15. Determine the perimeter and area of the right triangle cut by the line 3x + 4y –12 = 0 on the coordinate axes.
Solution:
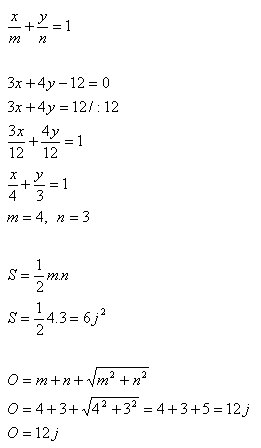
16. Write the equation of a line parallel to 5x + 12y -1 =0 and at a distance d = 5 from it.
Solution:
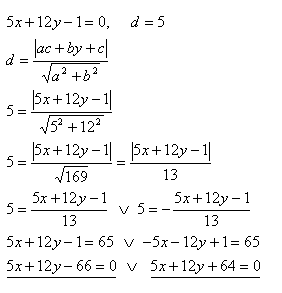
The required equations are 5x +12y - 66 = 0 and 5x +12y + 64 = 0
17. Calculate the distance from point A[2;-4] to the line 3x + 4y = 0.
Solution:
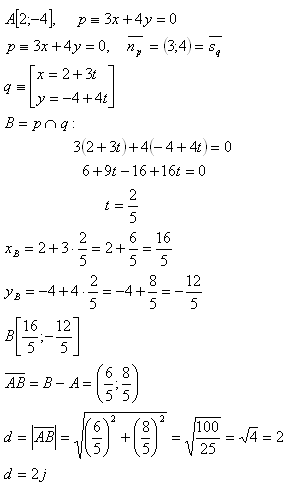
The distance from point A to line p is d = 2 units,
18. The diagonals of a rhombus u1 = 4, u2 = 6 lie on the coordinate axes (u1 on the x-axis). Write the equations of the lines on which the sides of the rhombus lie.
Solution:
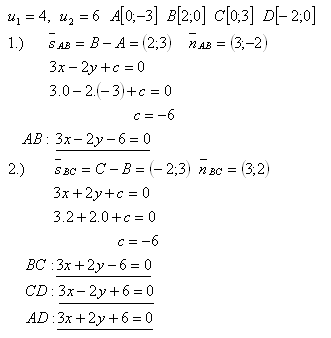
The equations of the sides of the rhombus are:
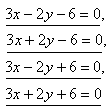
19. Determine the equation of a line passing through point [2;3] such that the segment on the x-axis is half the length of the segment on the y-axis.
Solution:
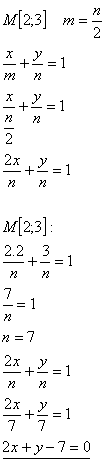
20. Given points A[3;-2], B[1;4], C[-1;-3]. Determine point D so that line CD intersects segment AB at its midpoint S and CD = 3·|CS|.
Solution:
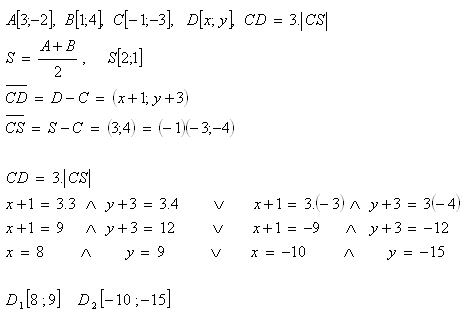
The condition is satisfied by two points D1[8 ; 9] and D2[-10 ; -15]. ⁞