Kirchhoff's laws
1.Explain the application of Kirchhoff's laws in electrical engineering.
Solution:
Kirchhoff's laws are used to solve a branched electrical circuit – (electrical network) that has multiple sources and resistors connected in various ways. A node is a point in the circuit where at least three conductors meet. A branch is a part of the electrical circuit between two nodes.
2.A current of 1.5A branches into two resistors connected in parallel R1 = 4Ώ and R2 = 6Ώ. What is the current in each resistor?
Solution:
Analysis:
I = 1.5A, R1 = 4Ώ , R2 = 6Ώ, I1 = ?, I2 = ?
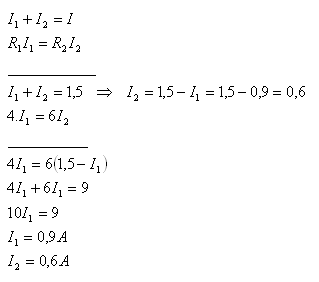
The currents through the resistors are I1 = 0.9A, I2 = 0.6A.
3.Two appliances with resistances R1 = 400Ώ and R2 = 600Ώ are connected in parallel and supplied with a voltage of 300V. Determine the electric currents through the appliances.
Solution:
Analysis:
R1 = 400Ώ, R2 = 600Ώ, U = 300V, R = ?, I = ?, I1 = ?, I2 = ?
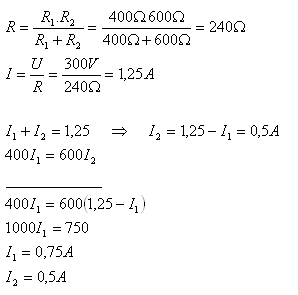
The currents through the appliances are I1 = 0.75A and I2 = 0.5A.
4.An ammeter has a range of 1.2A and a resistance of 0.02Ώ. What must be the shunt resistor so that currents up to 6A can be measured?
Solution:
Analysis:
I = 1.2A, RA = 0.02Ώ, I‘ = 6A, Rb = ?
The shunt resistor must be Rb = 0.005Ώ.
5.The voltmeter is designed for a maximum voltage of 10V and we want to measure voltages up to 100V. What will be the resistance of the series resistor if RV = 1kΏ?
Solution:
Analysis:
U‘ = 100V, U = 10V, RV = 1000Ώ, Rp = ?
The resistance of the series resistor will be 9kΏ.
6. Two resistors with resistances R1 = 5Ώ and R2 = 10Ώ are connected in parallel and connected to a constant voltage U = 4.5 V. Calculate the resulting resistance R, the total current I and the currents flowing through the individual resistors.
Solution:
7.Three resistors are connected in series. The voltage drop across resistor R1 = 36Ώ is U1 = 9V. Determine the voltage U2 across resistor R2 = 64 Ώ and the resistance R3, if the voltage at the terminals of the source is U = 120V.
Solution:
The voltage across resistor R2 is U2 = 16V. The third resistor has resistance R3 = 380 Ώ.
8.Three resistors with resistances R1 = 15Ώ, R2 = 21Ώ and R3 = 14Ώ are connected in series. What is the voltage across each resistor if the total source voltage is U = 40V? What is the magnitude of the current flowing through each resistor?
Solution:
The voltages across the individual resistors are U1 = 12V, U2 = 16.8V, U3 = 11.2V.
A current of 0.8A flows through each resistor.
9. A current I = 4A branches into three conductors with resistances R1 = 2Ώ, R2 = 5Ώ, R3 = 10Ώ. Calculate the total resistance of the circuit and the source voltage. What are the magnitudes of the currents in the individual conductors?
Solution:
The currents in the individual conductors are I1 = 2.5A, I2 = 1A, I3 = 0.5A.
10.Two resistors with resistances R1 and R3 are connected in series. The other two, R2 and R4, are also connected in series. Both branches of resistors are connected in parallel and connected to a source ( Ue = 6V, Ri = 0.2Ώ ). Calculate the currents flowing through the individual branches.
Solution:
11.From a source with voltage Ue = 150V( Ri = 0 ) a current passes through resistor R1 = 38Ώ. It then branches into resistors connected in parallel with resistances R2 = 20Ώ and R3 = 30Ώ. Calculate the currents in the individual branches of the circuit.
Solution:
12.Two bulbs with power ratings P1 = 45W and P2 = 5W are connected in parallel to a source through which a current I = 3A flows. Determine the currents that flow through the bulbs.
Solution:
The currents through the individual bulbs are I1 =2.7A and I2 = 0.3A.
13.Into how many equal parts must a wire with resistance R1 = 18Ώ be divided so that by connecting them in parallel we obtain a resistance R = 0.5Ώ.
Solution:
Analysis:
R1 = 18Ώ, R = 0.5Ώ, n = ?
Resistance of the whole wire R1, resistance of one part of the wire R = R1/n. Resistance of equal parts of the wire connected in parallel:
The wire must be divided into 6 equal parts.
14.What is the magnitude of the current in the branches if R1 = 4Ώ , R2 = 12Ώ and each cell has electromotive voltage Ue = 2V and internal resistance Ri = 0.5Ώ, n = 3
Solution:
