sk|cz|

Physics

Dynamics

1.With what magnitude of force does a person of mass 75 kg act on the floor of an elevator cabin when

  • a) the elevator is at rest
  • b) the elevator is moving vertically upward with acceleration  a = 2 m.s-2
  • c) the elevator is moving vertically downward with acceleration  a = 2 m.s-2 
      (g = 10 m.s-2)

Solution:

a)    F1 = m·g

F1 = 75 kg · 10 m.s-2 = 750 kg·m·s-2 = 750 N.

 

b) F2 = m · ( g + a )

F2 = 75 kg · 12 m.s-2 = 900 kg·m·s-2 = 900 N

 

c) F3 = m · ( g – a )

F3 = 75 kg · 8 m.s-2 = 600 kg·m·s-2 = 600 N


The acting forces are F1 = 750 N, F2 = 900 N, F3 = 600 N.

2.A constant force F = 18.2·10-20 N acts on an electron in an electric field in a vacuum. What speed will the electron acquire (me = 9.1·10-31 kg) if, starting from rest, it travels a distance of 1 cm?

Solution:

Analysis:

F = 18.2·10-20 N, me = 9.1·10-31 kg, s = 1 cm = 10–2 m.

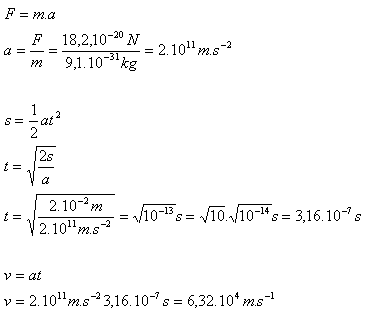
fyzika-dynamika-2 

The electron will acquire speed v = 6.32·104 m.s-1.

3.An aircraft of mass 12 t has a speed of 252 km.h-1. The engines exert a total thrust force of 20 kN on the aircraft. 30% of this force is used to overcome friction and air resistance. What must the runway length be?

Solution:

Analysis:

m = 12 t = 12 000 kg, v = 252 km.h-1 = 70 m.s-1,

F = 70% of 20 000 N = 0.7 · 20 000 N = 14 000 N

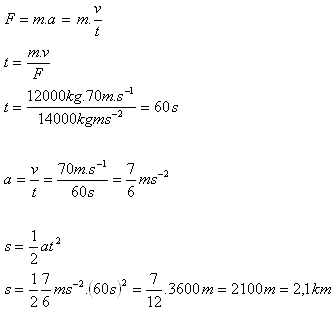
fyzika-dynamika-3

The runway length must be at least 2.1 km.

4. a) State the formulas for calculating the magnitude of the centrifugal (centripetal) force

b) What centripetal force acts on a small ball of mass 200 g attached to a string if the ball moves uniformly in a circle in the horizontal plane? The string length is 60 cm, speed 6 m.s-1.

Solution:

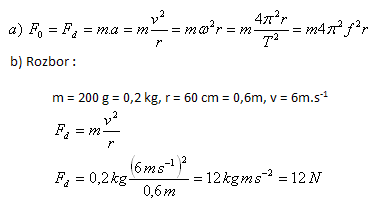
fyzika-dynamika-4

The centripetal force on the ball is 12 N.

5.During an aerobatic flight, an aircraft describes a vertical circle of radius 400 m at a speed of 360 km.h-1. With what pressing force does a pilot of mass 80 kg act on the seat at the highest and lowest points of the trajectory?

Solution:

Analysis:

v = 360 km.h-1 = 100 m.s-1, r = 400 m, m = 80 kg, g = 10 m.s-1

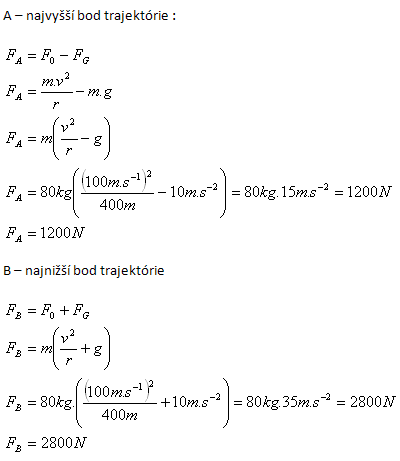
fyzika-dynamika-5
 

The pilot acts on the seat with force FA = 1200 N or FB = 2800 N.

6.A car of mass 1 000 kg has a speed of 54 km.h-1. It enters a bridge with a radius of curvature r = 50 m.

  • a)    With what pressing force did the car act on the road at the top of the bridge?
  • b)    What speed does the car have at the top of the bridge?
  • c)    What happens if the car’s speed is 90 km.h-1?

Solution:

Analysis: m = 1000 kg, v = 54 km.h-1 = 15 m.s-1, r = 50 m, v‘ = 90 km.h-1 = 25 m.s-1

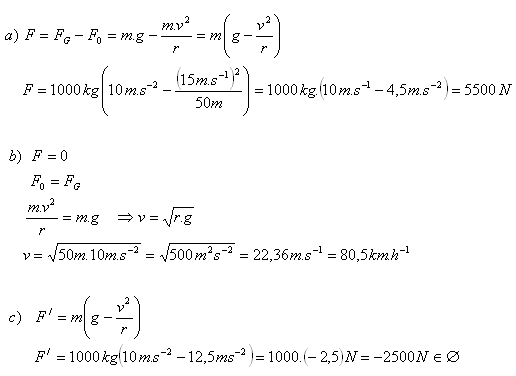
fyzika-dynamika-6 

  • a) F = 5500 N.
  • b) The speed is 80.5 km.h-1.
  • c) At 90 km.h-1 the car will lift off (a jump occurs). The car goes into projectile motion.

7.A car wheel has a mass of 6 kg. Its center of gravity is off the geometric center, therefore a centrifugal force F0 = 3.03 N acts at the center of gravity. How far is the center of gravity from the center if the wheel rotates at 96 rpm?

Solution:

Analysis:

m = 6 kg, F0 = 3.03 N, f = 96 rpm = 1.6 s-1

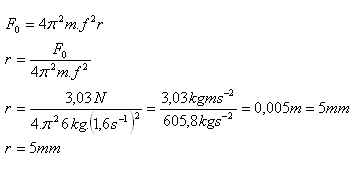
fyzika-dynamika-7

The distance of the center of gravity from the center is 5 mm.

8.Determine the acceleration of a body sliding (without friction) down an inclined plane of length l = 20 m with slope α = 5o. Also determine the speed of the body at the end of the incline.

Solution:

Analysis:

l = 20 m, α = 5o, g = 10 m.s-3

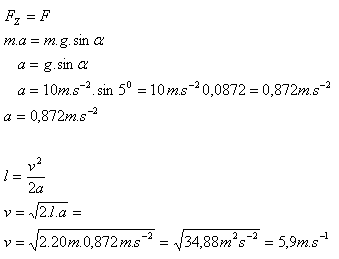
 fyzika-dynamika-8

The acceleration is a = 0.872 m.s-2. Its speed at the end of the incline is about 6 m.s-1.

9.What is the coefficient of kinetic friction between sleds of mass 400 kg and the surface if a friction force FT = 80 N must be overcome to keep the sleds moving uniformly? Also determine what load of wood the horses can pull on these sleds if their tractive force is F‘T = 1400 N.

Solution:

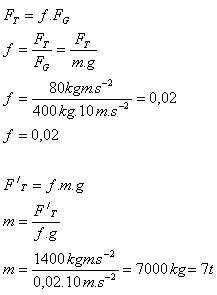
fyzika-dynamika-9 

The coefficient of friction between the sleds and snow is f = 0.02. The horses can pull 7 tonnes of wood.

10.A block of mass 5 kg is on an inclined plane with angle α = 30o and coefficient of kinetic friction f = 0.35. With what force must we act on the body so that it remains at rest?

Solution:

The equilibrium condition on an inclined plane is:

F = m g ( sin α – f cos α )

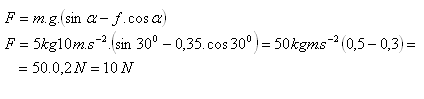
fyzika-dynamika-10 

The required force is F = 10 N.

11.Bulk material is stored in depots in cone-shaped piles. Compute the angle of slope that a freely poured material makes with the horizontal for

  • a)    coal: f = 1
  • b)    clay: f = 0.8
  • c)    sand: f = 0.68
(f – coefficient of kinetic friction)

Solution:

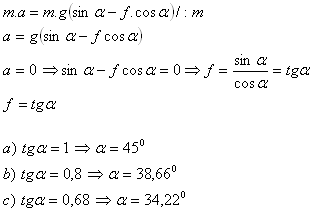
fyzika-dynamika-11 

The slope angles are: coal α = 45o, clay α = 38.66o, sand α = 34.22o.

12.Two bodies of masses m1 and m2 are connected over a pulley on an inclined plane. What must be the mass m2 if it is to keep the body of mass m1 = 8 kg at rest, when the incline angle is α = 40o and the coefficient of kinetic friction is f = 0.4 (g = 10 m.s-2)?

Solution:

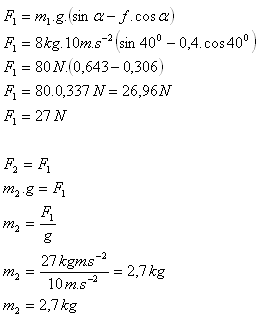
fyzika-dynamika-12 

The mass of the second body is m2 = 2.7 kg.

13.A car of mass 2 000 kg moves at constant speed uphill on a 4% grade. Determine the tractive force of the engine.

Solution:

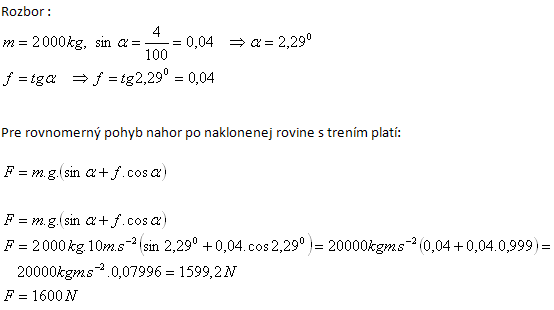
fyzika-dynamika-13 

The tractive force of the engine is 1600 N.

14.A car of mass 500 kg accelerates uphill on a 2% grade with constant acceleration a = 2 m.s-2. Determine the tractive force of the engine.

Solution:

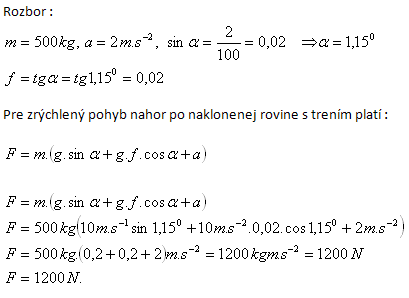
fyzika-dynamika-14 

The tractive force of the engine is 1200 N.

15.A car of mass 200 kg accelerates uphill (α = 5o, f = 0.09). What is the acceleration of the car if the engine’s tractive force is 653.3 N?

Solution:

Analysis.

m = 200 kg, F = 653.3 N, α = 5o, f = 0.09, FG = 2000 N, a = ?

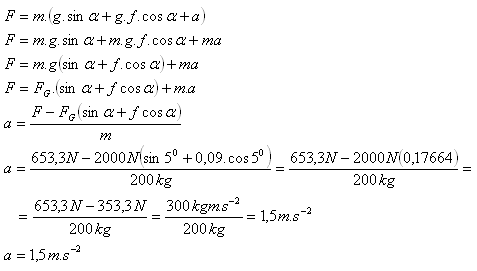
fyzika-dynamika-15 

The acceleration of the car is a = 1.5 m.s-2.

16.A bullet of mass 10 g is fired at a speed of 800 m.s-1 from a rifle of mass 4 kg. Compute the recoil speed of the rifle.

Solution:

Analysis:

m1 = 10 g = 0.01 kg, m2 = 4 kg, v1 = 800 m.s-1, v2 = ?

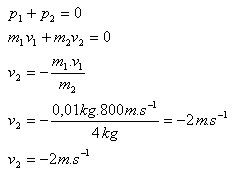
fyzika-dynamika-16

The recoil speed of the rifle is v2 = 2 m.s-1.

17.A submachine gun fires 600 rounds per minute. Each bullet has a mass of 4 g, and its speed when leaving the barrel is 500 m.s-1. Determine the average magnitude of the force with which the submachine gun presses on the shooter’s shoulder.

Solution:

Analysis:

600 / min = 600 / 60 s, 1 bullet per 60 / 600 s = 0.1 s. t = 0.1 s.

m1 = 4 g = 0.004 kg, v1 = 500 m.s-1

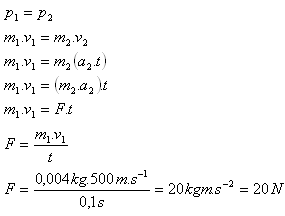
fyzika-dynamika-17 

The submachine gun presses on the shooter’s shoulder with an average force F = 20 N.

18.Two balls moving in the same direction collide. The first has mass 2 kg and moves at 2.5 m.s-1. The second has mass 8 kg. What was the speed of the second ball if after the collision they move together at 2.1 m.s-1?

Solution:


Analysis:

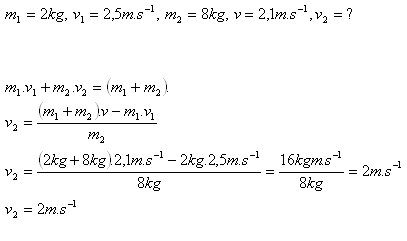
fyzika-dynamika-18 

The second ball was moving at speed v2 = 2 m.s-1.

19.A projectile of mass 100 kg flying along a railway line at 500 m.s-1 strikes a wagon with sand of mass 10 t and remains embedded in it. What speed will the wagon have after the impact if before the collision it was moving at 36 km.h-1

  • a)    against the projectile
  • b)    in the direction of the projectile

Solution:

Analysis:

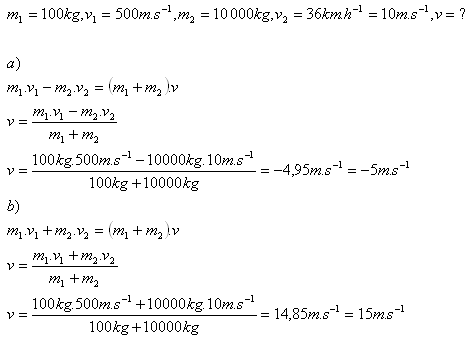
fyzika-dynamika-19

20. A boy of mass 60 kg stands on skates on smooth ice. He starts moving by throwing away an ice block of mass 6 kg at speed 3 m.s-1. How far will the boy travel due to the throw if he moves for 9 seconds?

Solution:

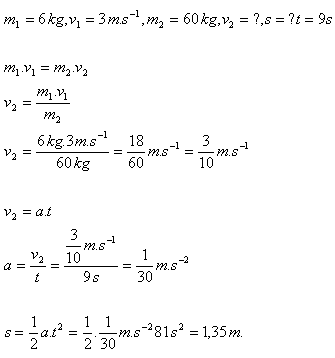
fyzika-dynamika-20 

The skater travels a distance of 1.35 m.

21.One stage of the Tour of Slovakia cycling race was a short uphill sprint. The cyclists moved along a straight road with a grade p = 7.5%. The horizontal distance between start and finish is s = 825 m. The stage winner moved at uniform speed and delivered an average power P = 350 W. The mass of the cyclist including the bike is m = 68 kg.

  • In what time t did the winner complete the stage?
  • What average speed v did he maintain during the race?

Solution:

dynamika-21a

The winner completes the stage in 120.45 s, i.e., in 2 minutes. During the race he moved at an average speed of 6.87 m.s-1, i.e., 24.7 km.h-1.

 

This solution was sent to us by Jakub Hrdina, thank you.