Ludolf's number in China

Ancient Chinese mathematics.

Babylonian and Egyptian mathematics developed along the banks of the great rivers Euphrates, Tigris, and Nile. Similarly, along the banks of the great river Yangtze lived highly civilized nations with rich mathematical knowledge — the Chinese. Around 200 B.C., Zhang Cang created the central work of Chinese mathematics, “The Nine Chapters on the Mathematical Art,” which was supplemented, commented on, and rewritten by Chinese mathematicians over several centuries. In their works, π = 3.

Zhang Heng (78–139 A.D.) came to the conclusion that “the ratio of the square of the circumference of a circle to the square of the perimeter of the square circumscribed around that circle is 5:8.”

 

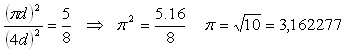
One of the greatest ancient Chinese mathematicians, the commentator and editor of “The Nine Chapters on the Mathematical Art,” Liu Hui (5th century A.D.), contributed to an approximate value of the number π. In his method, the area of a circle is replaced by the area of inscribed and circumscribed n-gons. He emphasized: “The finer we divide the sides of the n-gons, the more their perimeters will approach the length of the circumference.” In his calculation, he used 3,072-sided polygons and determined π = 3.14159.

Another prominent Chinese mathematician, Zu Chongzhi (430–501), expressed the value of π using a fraction: π = 355/113 = 3.141592, which he wrote in the decimal system as: π = 3 zhang 1 chi 4 cun 1 fen 5 li 9 hao 2 miao. The verbal notation of the place values was later omitted, and only the digits were written. The decimal point was replaced by the symbol “tien.” The entire history of mathematics in China testifies to the remarkable level of its creators. Mathematicians from Japan, India, Islamic countries, and Europe drew upon their knowledge.

---