Ludolf's number in ancient Greece

In continuation of our previous article, we will look at how different ancient nations dealt with the value of Ludolph’s number π.

Ancient Greek mathematics.

Thales of Miletus, Democritus of Abdera, Pythagoras of Samos, and Euclid were famous names of the brilliant philosophers and mathematicians of that period. Especially Euclid’s work “Elements” was considered “the most learned work after the Bible.” Archimedes of Syracuse (around 287–212 B.C.) in his work “Measurement of a Circle” assumed that “the ratio of the area of a circle to the square of its diameter is approximately equal to 11:14.”

 

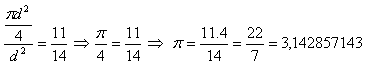
Claudius Ptolemy (85–165 A.D.), known for his geocentric model of the universe, published around the year 140 a work titled “The Great Compilation,” known by its Arabic name “Almagest.” In it, the author states:

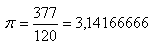
Let us now turn away from the ancient Greek mathematicians and ask ourselves the question: “Can an incorrect mathematical procedure lead to an approximately correct result?” It can!!! The Dutch mathematician Valentin Otho (1550–1603) was certainly familiar with both Archimedes’ and Ptolemy’s values of π. By using an unorthodox and incorrect subtraction of these values, he obtained:

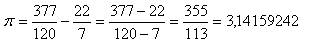
He achieved an accuracy up to six decimal places.

Roman mathematics.

The Roman contribution to mathematics is almost zero. V.P. Marcus (50 B.C.–15 A.D.) in his work “Ten Books on Architecture” stated: “For a wheel whose diameter is four and one-sixth feet, the circumference measures twelve and one-half feet.”

 

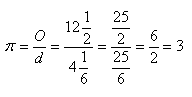
In this work, we can observe how mathematical knowledge in Europe began to decline more and more. The center of mathematical research began to shift to China, India, and Central and Minor Asia.

---