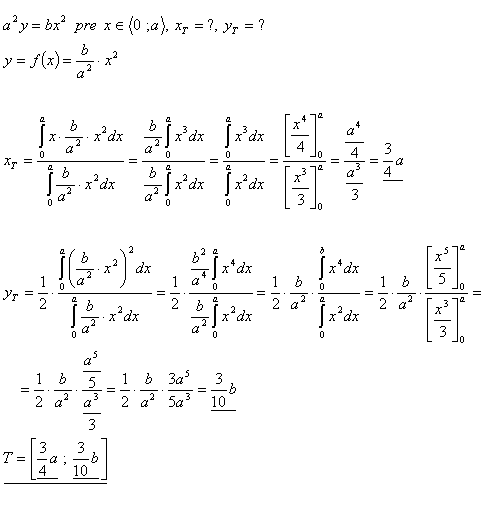Definite integral in physics
1.A particle moves in a straight line with acceleration a = 2.6 m.s-2. Determine the velocity equation and the displacement equation (if v0 = 0, s0 = 0). Calculate the velocity and displacement at time t = 2s.
Solution:
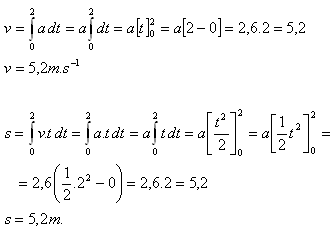
2.Determine the work required to stretch a spring by 25 cm from its unstretched state, given that a force of 16 N, parallel to the spring’s axis, stretches it by 80 cm.
Solution:
F = 16 N, x = 80 cm = 0.8 m, a = 0, b = 25 cm = 0.25 m.
The force F is directly proportional to the extension x
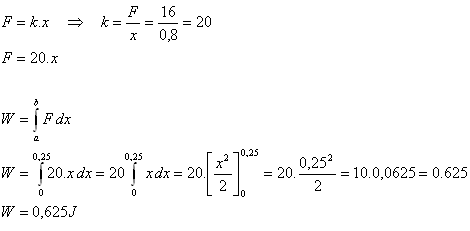
3.Determine the effective value of an alternating sinusoidal current
Solution:
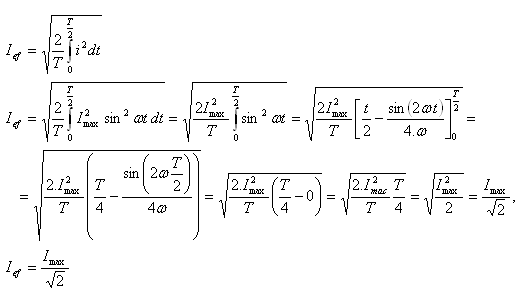
4.An alternating electric current with maximum value Imax flows through a stove coil with resistance R. Derive the formula for calculating the amount of Joule heat. The instantaneous current is: i = Imaxsin ωt.
Solution:
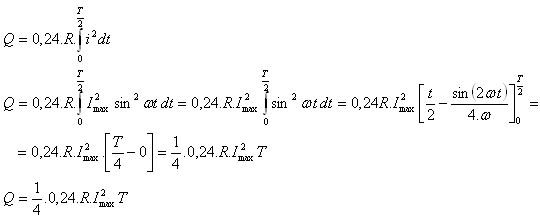
5.What distance is traveled by a body moving with velocity v = At2 + Bt + C during the first 10 seconds of motion, if:
- A = 3ms-1
- B = 1ms-1
- C = –1ms-1
Solution:
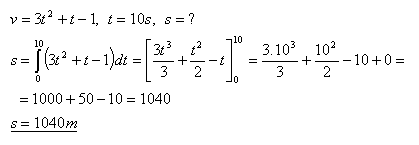
The body travels a distance of 1040 meters in 10 seconds.
6.Calculate the distance traveled by a raindrop in the first 6 seconds. Neglect air resistance.
Solution:
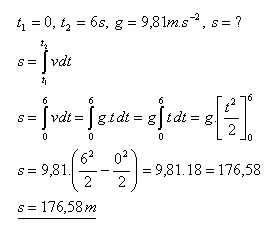
The raindrop travels 176.58 m in 6 seconds.
7. What work must be done for a body of mass m to increase its speed from v1 to v2?
Solution:
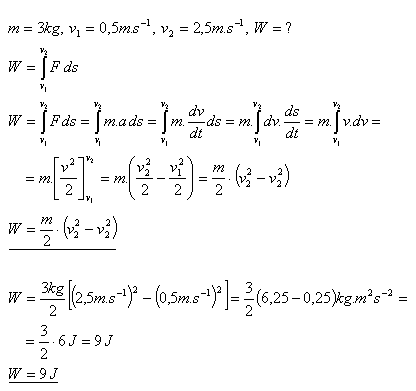
To increase the speed of the body, the work W = 9J must be done.
8.What work is done by an external force when stretching a steel rod of length l0 = 2m and cross-sectional area
S = 5mm2 by 1 mm with elastic deformation?
Solution:
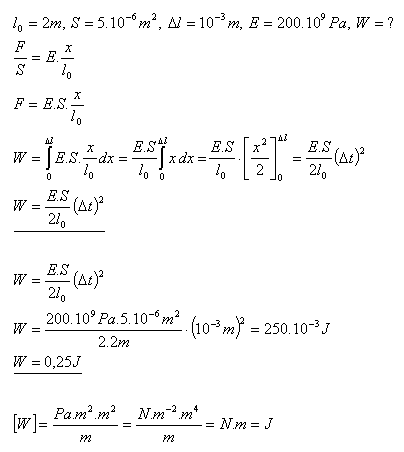
The external force does work W = 0.25J when stretching the steel rod.
9.Calculate the work required to lift a body of mass m to a height h above the Earth’s surface. Use the relation:
Solution:
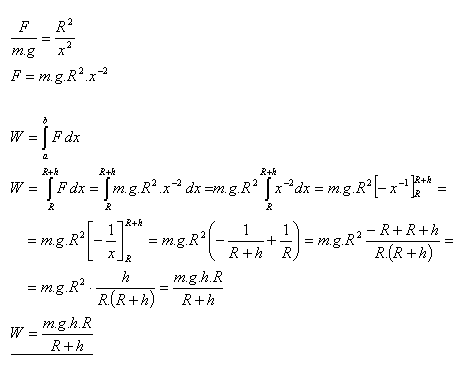
The work required to lift the body to height h above the Earth’s surface is:
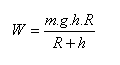
10. How long will it take for water, poured into a cylindrical vessel with base area S = 420cm2 and water height h = 40cm, to flow out through an opening at the bottom. The opening has area s = 2cm2. The outflow velocity is given by:
Solution:
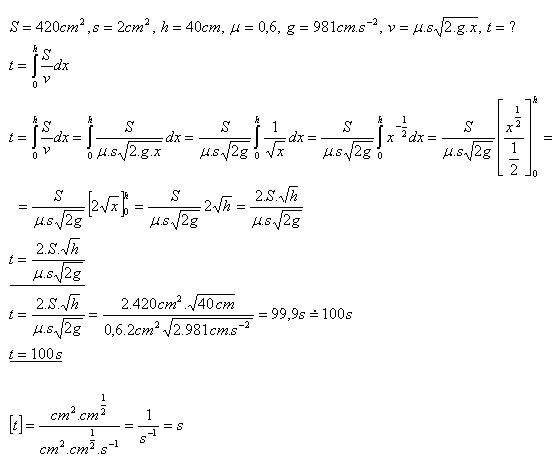
The water flows out in 100 seconds.
11.Calculate the coordinates of the centroid of a square with side a = 6 cm.
Solution:
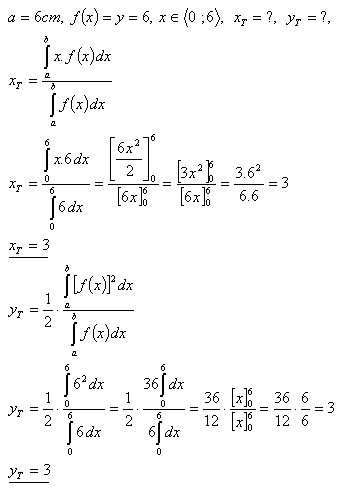
The centroid of the square has coordinates T = [3 ; 3]
12.Calculate the coordinates of the centroid of the plane figure bounded by the function:
- f(x) = y = x3, for x ∈ <0 ,1>
Solution:
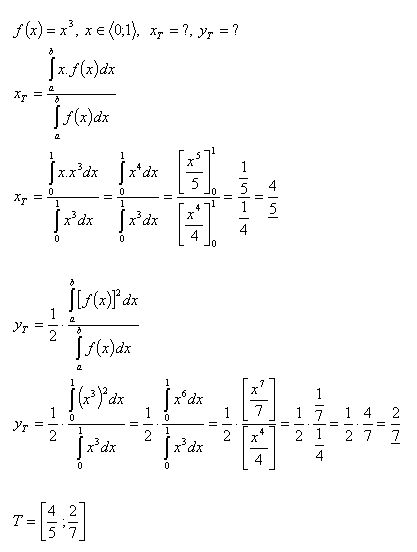
13. Calculate the coordinates of the centroid of the plane figure bounded by:
- the parabola y = x2
- and the lines y = 0, x = 1.
Solution:
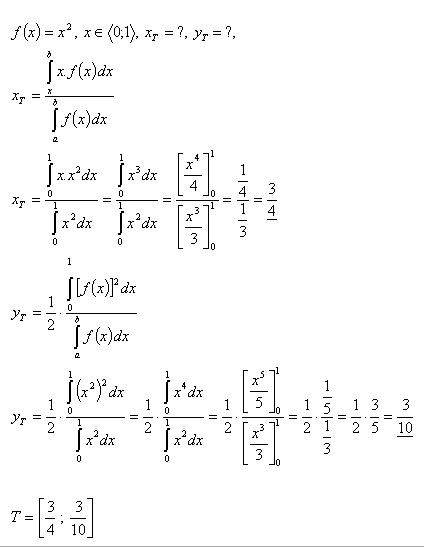
14.Determine the coordinates of triangle ΔABO formed by
- the line y = –x + 6 in the coordinate system. A[6 , 0], B[0 ,6], O[0, 0]
Solution:
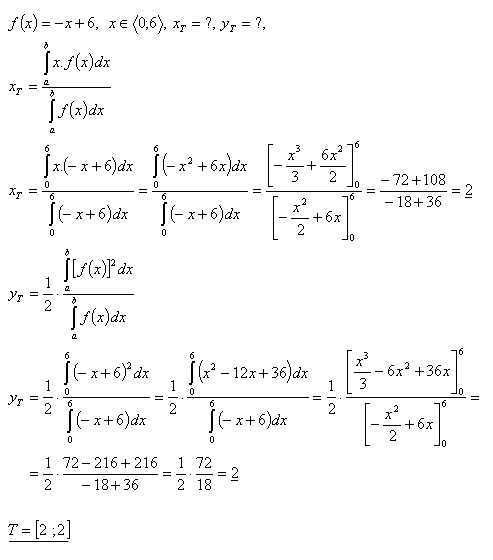
15. Find the coordinates of the centroid of the plane figure bounded by the curve:
- a2y = bx2 for x ∈ < 0 ; a >
Solution: