Extremes - practical problems
1.Split the number 32 into two addends so that their product is maximal.
Solution:
First addend: x x = 16
Second addend: 32 – x 32 – 16 = 16
y = x.(32 – x)
y = 32x – x2
y‘ = 32 – 2x
32 – 2x = 0
2x = 32
x =16
y‘‘ = -2 < 0 - maximum
The first addend is 16, the second is also 16
2.Split the number 16 into two addends so that the sum of the squares of these addends is minimal.
Solution:
First addend: x x = 8
Second addend: 16 – x 16 – 8 = 8
y = x2 + ( 16 – x )2
y = x2 + 256 -32x +x2
y = 2x2 – 32x + 256
y‘ = 4x – 32
4x - 32 = 0
4x = 32
x = 8
y‘‘ = 4 > 0 - minimum
The first addend is 8, the second is also 8.
3.Find a positive number x such that the sum of this number and its reciprocal is minimal.
Solution:
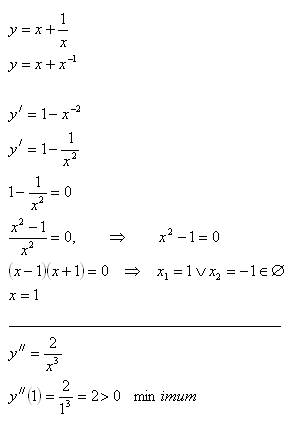
The sought number is x = 1.
4.From a wire of length l = 120 cm we must make a model of a rectangular prism with a square base. What should its dimensions be so that the surface area is maximal?
Solution:
Edge of the square base: a = b = x
Height of the prism: c
8x + 4c = l
8x +4c =120/:4
2x + c = 30
c = 30 – 2x
S = 2( ab + ac + bc )
S = 2( x.x + x(30 – 2x) + x(30 – 2x))
S = 2(-3x2 +60x )
S = -6x2 +120x
S‘ = -12x + 120 S‘‘ = -12 < 0 maximum
-12x + 120 = 0
12x = 120
x = 10
c = 30 -2x = 30 – 2·10 = 10
x = 10 cm, c = 10 cm .
The prism must be a cube with edge x = 10 cm
5.A rectangular garden has perimeter 200 m. Determine the dimensions of the garden so that its area is maximal.
Solution:
a = x
P = 2a + 2b
200 = 2x +2b/:2
100 = x + b
b = 100 – x b = 100 – x = 100 – 50 = 50
b = 50 m
S = a.b
S = x.(100 – x )
S = 100x – x2
S‘ =100 – 2x S‘‘ = -2 < 0 - maximum
100 – 2x = 0
2x = 100
x = 50
a = 50 m
The garden will have maximal area if it is a square with sides a = b = 50 m.
6.When does a rectangular prism with volume V = 63 cm3 and height v = 7 cm have the smallest surface area?
Solution:
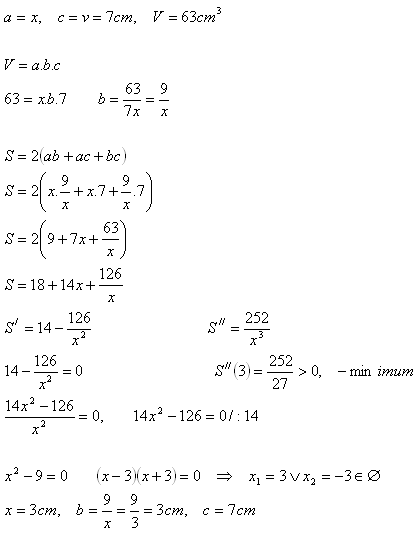
The dimensions of the sought prism are a = 3 cm, b = 3 cm, c = 7 cm
7.On the riverbank a rectangular garden must be fenced (one side of the rectangle is formed by the river) with wire of length l = 800 m. What dimensions must the garden have so that its area is maximal?
Solution:
800 = 2a + b
a = x
b = 800 – 2a = 800 – 2x
S = a.b
S = x.(800 – 2x)
S = 800x – 2x2
S‘ =800 – 4x S‘‘ = -4 < 0 - maximum
800 – 4x = 0
4x = 800
x = 200
x = 200 m
b = 800 – 2x
b = 800 – 400 = 400
b = 400 m
The garden dimensions are a = 200 m, b = 400 m.
8.What are the dimensions of an open pool with a square bottom if the pool has volume V = 32 m3 and the amount of material for its construction should be minimal.
Solution:
V = 32 m3, x – edge of the square base, v – height of the prism
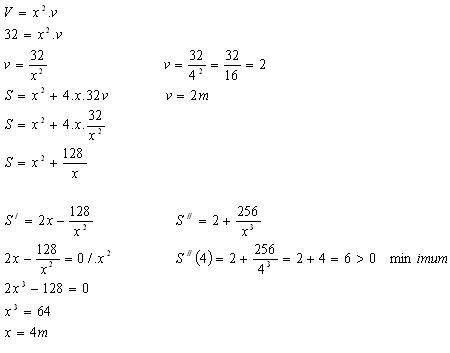
Dimensions: a = 4 m, b = 4 m, v = 2 m
9.A wire of length 5 m is bent at a right angle so that the distance between its two ends is minimal. Where should the wire be bent?
Solution:
Legs a = x, b = 5 – x
Hypotenuse c = y
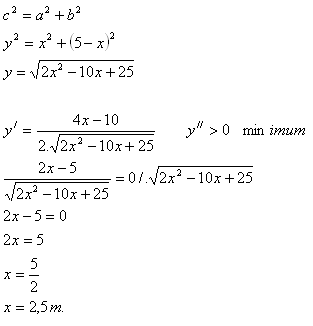
The wire should be bent at the midpoint.
10.From a square sheet of metal with side 30 cm four equal small squares must be cut out at the corners, and the remainder folded to form an open box. Determine the side x of the cut-out squares so that the box volume is maximal.
Solution:
a = 30 – 2x, b = 30 – 2x, c = x
V = a·b·c
V = (30 – 2x)(30 – 2x)·x
V = 4x3 – 120x2 +900x
V‘ = 12x2 – 240x +900 V‘‘ = 24x -240
12x2 – 240x +900 =0 /:12 V‘‘(5) = 24·5 -240 = -120 < 0 maximum
x2 - 20x + 75 = 0
( x – 5 )( x -15 ) = 0 x1 = 5 x2 = 15 - not acceptable
x = 5 cm
The side of the cut-out square is x = 5 cm.
11.A pit with volume 500 m3 has the shape of a rectangular box with a square base of side x and depth h. For which dimensions x and h will the pit have minimal surface area?
Solution:
Analysis:
V = 500 m3, x = ?, h = ?
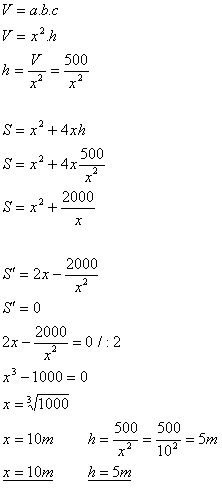
The pit has base a square with side x = 10 m and height h = 5 m.
12.Given the parabola y = 4 – x2. Find the vertices of the rectangle ABCD with the largest perimeter whose vertices A, B lie on the x-axis, vertices C, D have positive y-coordinates and lie on the parabola.
Solution:
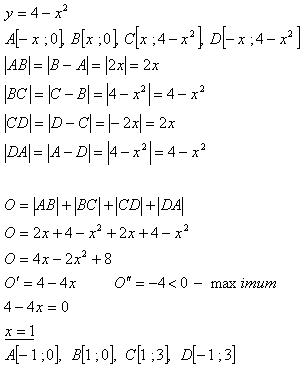
The points are: A[-1;0], B[1;0], C[1;3], D[-1;3]
13.Determine the dimensions (r, v) of a cylindrical vessel without a lid whose surface area is S = 27π so that its volume is maximal.
Solution:
Analysis:
S = 27π, r = x
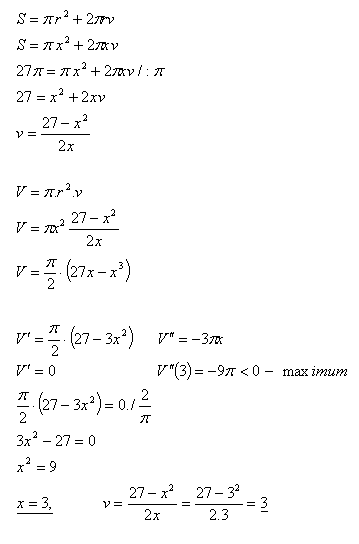
The dimensions of the vessel are r = x = 3 cm, v = 3 cm.
14.An open-top cylindrical container has volume V = 3140 cm3. Determine the cylinder dimensions (r, v) so that the least amount of material is used to make it.
Solution:
Analysis:
V = 3140 cm3, r = x = ?
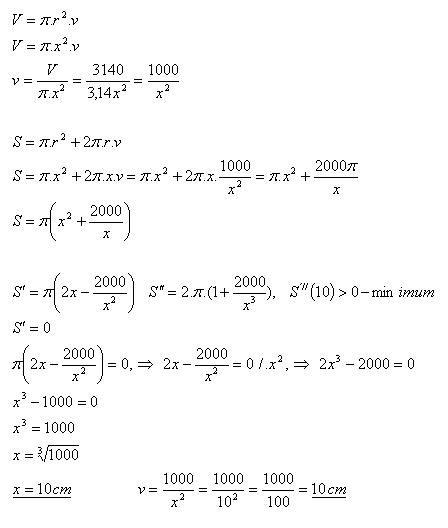
The dimensions of the vessel are r = x = 10 cm, v = 10 cm.
15.What dimensions must a rectangle with perimeter P = 40 cm have so that its diagonal is minimal?
Solution:
Analysis:
x = a = ?, b = ?
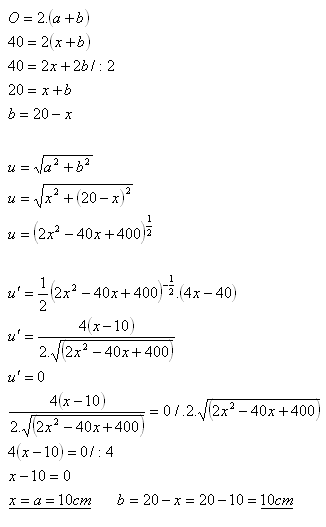
The figure is a square with side a = 10 cm.