sk|cz|

Physics

Particle charge in a magnetic field

1. Explain the behavior of a charged particle in a magnetic field!

Solution:

particle-in-magnetic-field-1
 

2. Derive the formula for the radius of the circular trajectory of a charged particle in a homogeneous magnetic field!

Solution:

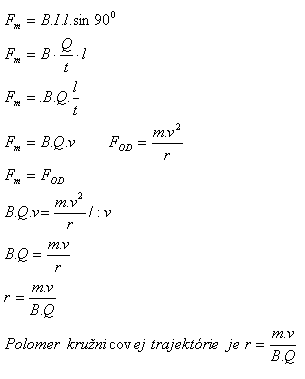
particle-in-magnetic-field-2.gif

3. With what velocity did a proton (mp = 1.673·10–27kg, Qp = 1.602·10-19C) move in a magnetic field (B = 1T) if its trajectory was a circle with radius r = 60cm? With what frequency did the proton orbit the circle?

Solution:

Analysis:

mp = 1.673·10–27kg, Qp = 1.602·10-19C,  B = 1T, r = 60cm = 0.6m,  v = ?,  f = ?

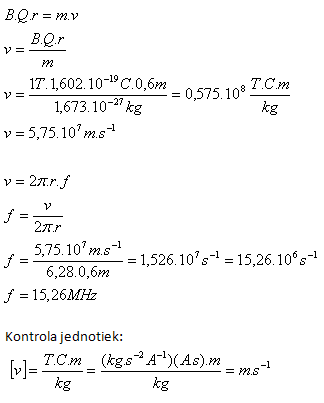
particle-in-magnetic-field-3.gif 

The velocity of the proton in the magnetic field was 5.75·107m·s-1, its frequency f = 15.26 MHz.

4. What kinetic energy does a proton (mp = 1.673·10-27kg, Qp = 1.602·10-19C) have when moving in a circle of radius r = 10cm in a homogeneous magnetic field with B = 0.1T, perpendicular to the induction lines?

Solution:

Analysis:

mp = 1.673·10-27kg, Qp = 1.602·10-19C,  r = 10cm = 0.1m,  B = 0.1T,  Ek = ?

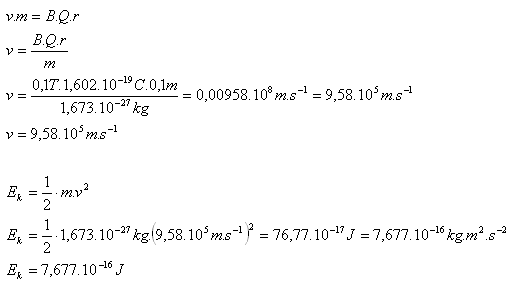
particle-in-magnetic-field-4.gif 

The kinetic energy of the proton is Ek = 7.677·10–16J.

5. An electron (me = 9.1·10–31kg, Qe = 1.602·10–19C) after being accelerated in an electric field with U = 100V enters a homogeneous magnetic field with B = 10mT perpendicular to the induction lines. Along what trajectory will the electron move?

Solution:

Analysis:

me = 9.1·10–31kg, Qe = 1.602·10–19C,  U = 100V,  B = 10mT =10–2T

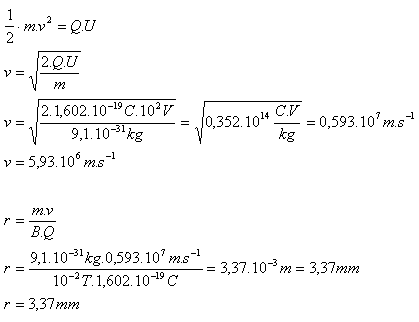
particle-in-magnetic-field-5.gif 

The electron will move in a circle with radius r = 3.37mm.

6. What magnitude must the magnetic induction of a homogeneous magnetic field have so that an electron moves in it in a circle with radius r = 40cm at velocity v = 3.8·107m·s-1? What will be the kinetic energy of the electron?

Solution:

Analysis:

r = 40cm = 0.4m,  v = 3.8·107m·s-1,  me = 9.1·10–31kg,  Q = e = 1.602·10–19C

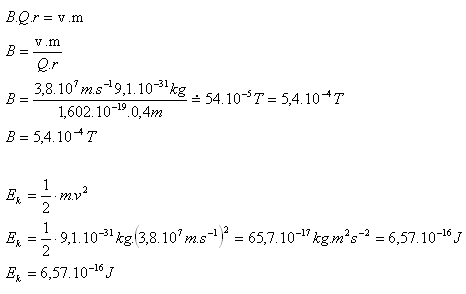
particle-in-magnetic-field-6.gif 

  • The magnetic induction must have magnitude B = 5.4·10–4T.
  • The electron has kinetic energy Ek = 6.57·10–16J.

7. With what velocity would a proton (mp = 1.673·10–27kg, Qp = 1.602·10–19C) have to move in the Earth's magnetic field (B = 5·10–5T – tables) perpendicular to the induction lines so that the magnetic force equals the gravitational force acting on it?

Solution:

Analysis:

B(Earth) = 5·10–5T,  mp = 1.673·10–27kg,  Qp = 1.602·10–19C,  g = 10m·s-2

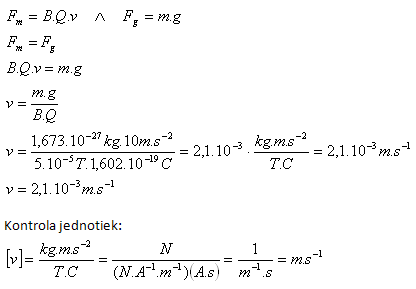
 particle-in-magnetic-field-7.gif

In the Earth's magnetic field the proton would have to move at velocity v = 2.1·10-3m·s–1.

8. Into a homogeneous magnetic field with B = 2·10–5T in a vacuum entered a proton (mp = 1.673·10–27kg, Qp = 1.602·10-19C) in a direction perpendicular to the induction lines. What will be the frequency of its circular motion?

Solution:

Analysis:

2·10–5T,  mp = 1.673·10–27kg, Qp = 1.602·10-19C,  f = ?

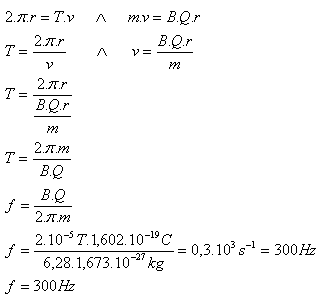
particle-in-magnetic-field-8.gif 

Check the units yourself.

The frequency of the electron’s circular motion will be f = 300Hz.

9. Two electrons moving with the same velocities entered two homogeneous magnetic fields (B1 = 0.1T, B2 = 0.2T) and began moving in circular trajectories. Determine the ratio of their orbital periods T1 : T2.

Solution:

Analysis:

B1 = 0.1T, B2 = 0.2T,  T1 : T2 = ?

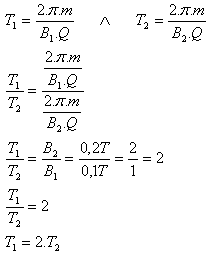
 particle-in-magnetic-field-9.gif

The ratio of the periods of the two electrons is T1 : T2 = 2 : 1

10. An electron started moving from rest and after passing through a potential difference of 220V entered perpendicularly into a homogeneous magnetic field with induction 5mT. In the magnetic field the electron moved in a circular trajectory with radius 1cm. Determine the mass of the electron.

Solution:

Analysis:

U = 220V,  B = 5·10–3T,  r = 1·10–2m,  Q = e =1.602·10–19C,  me = ?

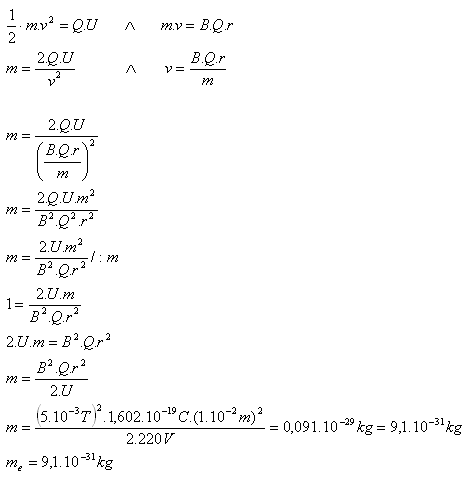
 particle-in-magnetic-field-10.gif

The mass of the electron is me = 9.1·10–31kg.

 

 


```