Astrophysics
1.How are distances, masses, and brightness of stars determined in astrophysics?
Solution:

2.How is information about stars and the universe obtained?
Characterize:
- Wien’s displacement law
- Stefan–Boltzmann law
- Radiant flux
- Radiant power
- Characteristics of the Sun
- Expansion of the universe
Solution:

Hubble’s law:
3.Calculate how long it takes light in vacuum to travel a distance equal to
- a) the diameter of the Solar System (s = 80 AU)
- b) the diameter of the Galaxy (s = 30 kpc)
Solution:
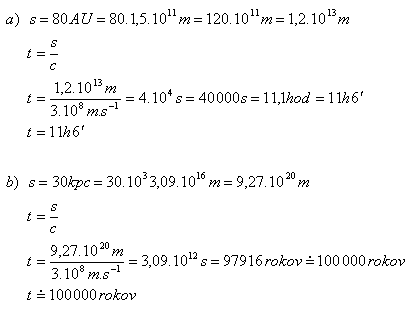
Light travels the diameter of the Solar System in 11 hours, the diameter of the Galaxy in about 100,000 years.
4.Calculate the average density of matter in the Solar System. Assume all the mass of the system is in the Sun (Mo = 2·1030kg) and that the Solar System is a sphere with radius R = 40 AU.
Solution:
Analysis:
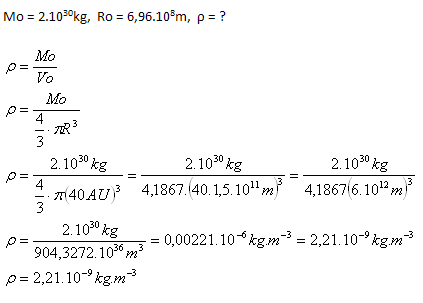
The density of matter in the Solar System is ρ = 2.21·10–9kg·m–3
5.The Sun orbits the center of the Galaxy at v = 250 km·s-1, approximately in a circle with radius r=10 kpc. Determine the orbital period of the Sun. What gravitational force attracts the Sun to the center of the Galaxy?
Solution:
Analysis:

- The orbital period of the Sun around the center of the Galaxy is about 250 million years.
- The Sun is attracted to the center of the Galaxy by a gravitational force Fg = 4·1020N.
6.Consider a globular cluster with mass MGC = 2·105Mo orbiting the center of the Galaxy (MG=1.4·1011Mo) in a circle of radius r=12 kpc. Determine:
- a) the force with which the cluster is attracted to the center of the Galaxy
- b) the centripetal acceleration of the cluster
- c) the velocity of the cluster relative to the center of the Galaxy
Solution:
Analysis:

- The force attracting the cluster to the center of the Galaxy is Fg = 5.4·1025N
- The centripetal acceleration of the cluster is a = 1.4·10–10m·s-2
- The velocity of the cluster relative to the center of the Galaxy is v = 228 km·s-1
7.Derive the formula for calculating the mass of a star (planet) using its satellite.
Solution:
Analysis:
M = mass of the star, m = mass of the satellite, r = radius of the satellite’s circular orbit, T = orbital period of the satellite, κ = 6.67·10–11N·m2·kg-2
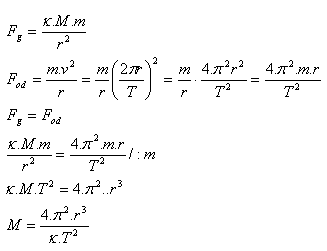
The mass of the star is calculated according to:
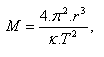
8.Calculate the mass of the planet Mars using its moon Deimos, which orbits Mars in a circle of radius r = 23.5·106m, with an orbital period of 1.26 Earth days.
Solution:
Analysis:
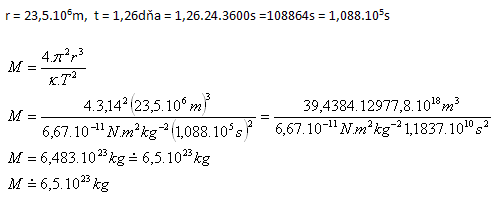
The mass of Mars is M = 6.5·1023kg.
9.Jupiter’s moon Europa orbits Jupiter in a circle with radius r1 = 6.71·108m and orbital period T = 3.88 days. Calculate how many times the mass of Jupiter is greater than the mass of Earth.
Solution:
Jupiter + Europa: M1 + m1, r1 = 6.71·108m, T1 = 3.88 days,
Earth + Moon: M2 + m2, r2 = 3.844·108m = 1 month = 30 days
m1 – negligible, m2 – negligible compared to M1 and M2
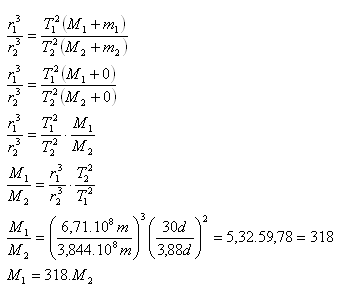
The mass of Jupiter is 318 times greater than that of Earth.
10.The total mass of a binary star is 3.5Mo, the components orbit their common center of mass with period T = 320 years. Determine the mutual position of the components perpendicular to the line of sight, which we would see under an angle π = 3.1″ and the distance of the binary star from the Sun.
Solution:
Analysis:
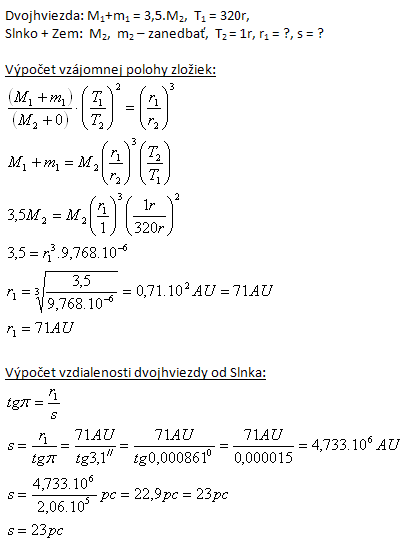
11.The apparent stellar magnitude of the Sun is -26.8m. Calculate its absolute magnitude M.
Solution:
Analysis:
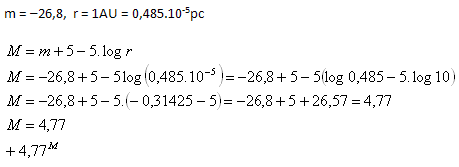
The absolute stellar magnitude of the Sun is +4.77M.
12.To what distance can we use a supernova to measure galaxy distances if its maximum absolute magnitude is –16M and we have a telescope observing stars up to apparent magnitude +22m?
Solution:
Analysis:
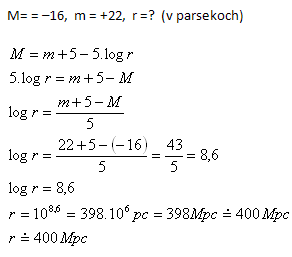
The telescope can be used up to a distance of about 400 Mpc.
13.What parallax π does a star have if the difference between its apparent and absolute magnitudes is +8?
Solution:
Analysis:

The star has a parallax π = 0.0025″.
14.What is the wavelength at which maximum radiation occurs and the intensity of radiation of a star with temperature 30,000K?
Solution:
Analysis:
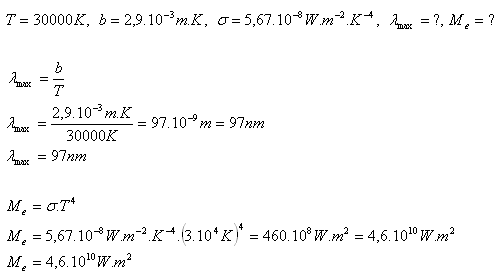
The wavelength is λ = 97nm, the intensity of radiation of the star is Me = 4.6·1010W·m2.
15.A red giant has surface temperature 3500K, radius R = 36Ro, mass M = 3.6Mo. Calculate its average density ρ and radiant power L. (σ = 5.67·10-8W·m-2·K–4)
Solution:
Analysis:

The average density of the Red Giant is ρ = 0.11 kg·m-3 and its radiant power L = 671·1028W.
16.Calculate the radius and average density of a white dwarf with mass M = 2.35Mo, surface temperature T = 12,500K, radiant power L = 0.0036Lo. Ro = 6.96·108m, T0 = 5780K
Solution:
Analysis:

The radius of the white dwarf is R = 9·106m and its average density ρ = 2.28·108kg·m–3.
17.What radiant flux from the Sun falls on an area of S = 1m2 (Radiant power of the Sun L=3.83·1026W)
- on Venus (r = 0.72AU)
- on Jupiter (r = 5.2AU)
Solution:
Analysis:
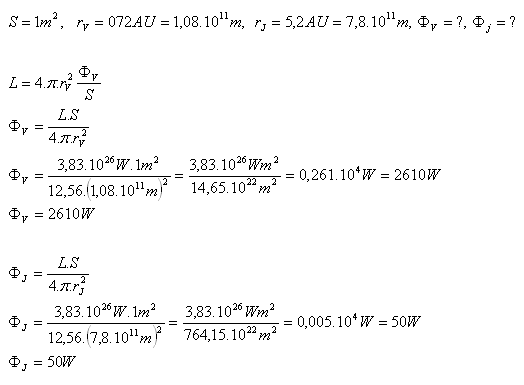
- The radiant flux on 1m2 of Venus is ФV = 2610W,
- on 1m2 of Jupiter is ФJ = 50W.
18.A star has apparent magnitude m1=4. What would be its apparent magnitude m2 if it were at twice the distance?
Solution:
Analysis:
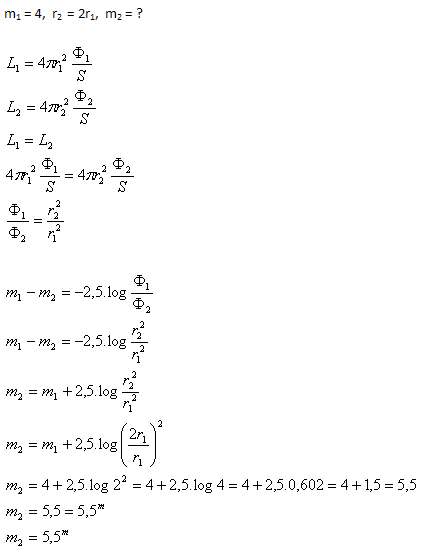
At twice the distance, the apparent magnitude of the star would be 5.5m.
19.Consider a distant galaxy that is moving away from our Galaxy with a velocity v = 6000 km·s-1. What wavelength of the hydrogen spectral line will we measure if its original wavelength is 656.3 nm? At what distance from us is this galaxy likely located?
Solution:
Analysis:
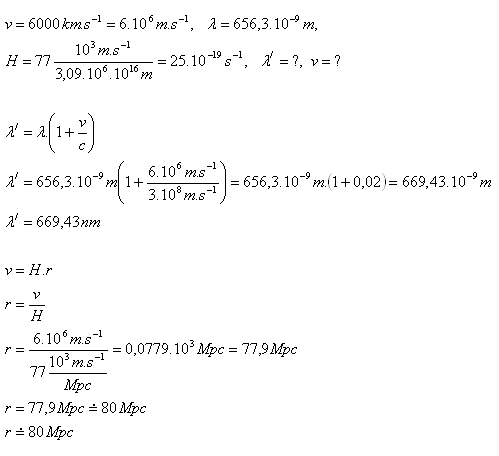
The wavelength increases to a value of λ' = 669.43 nm. The galaxy is about 80 Mpc away from us.
20.Determine the time over which our universe has been expanding. Determine the time that has elapsed from the “Big Bang” to the present.
Solution:
Analysis:
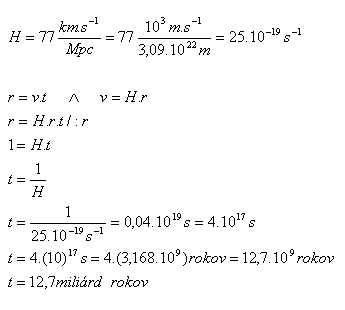
About 13 billion years have passed since the “Big Bang.” The calculation depends on the choice of the Hubble constant H.
For H it holds: 16.13·10–19s-1 < 25·10-19s-1 < 32.26·10–19s-1.