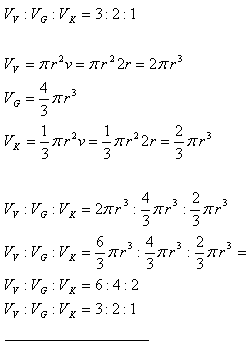Evidence
1. How do we prove the truth of a mathematical statement?
Solution:


2.Prove the statement by direct proof:
Solution:
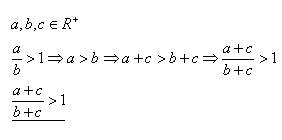
What holds according to the assumption.
3.Prove the statement by direct proof:
Solution:
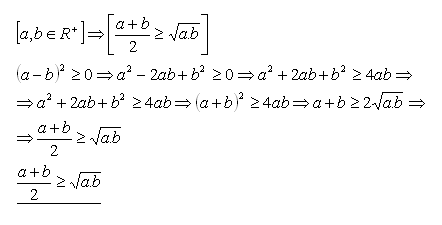
It holds for all a, b ∈ R+
4.Prove the statement by direct proof:
Solution:
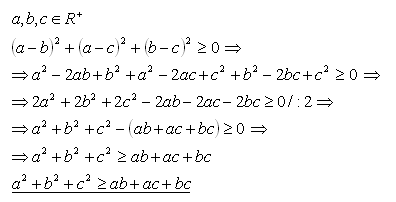
It always holds, because the sum of the squares of three real numbers is always positive. Equality holds when a = b = c.
5.Prove the statement by direct proof:
Solution:
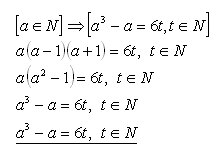
The statement holds. Of three consecutive natural numbers (a – 1), a, (a + 1), one is divisible by 2 and one is divisible by 3. Hence their product is divisible by 6.
6.Prove the statement by indirect proof: If a2 is a natural number divisible by 3, then a is a natural number divisible by 3.
Solution:
B‘ => A‘:
If a is not divisible by 3, then a2 is not divisible by 3.
1) a = 3k + 1
a2= (3k + 1 )2
a2= 9k2 +6k +1
a2= 3(3k2 + 2k) +1
a2= 3m + 1 – holds for m = 3k2 +2k
2) a = 3k + 2
a2= (3k + 2)2
a2= 9k2 +12k +4
a2= 3(3k2 +4k +1) +1
a2= 3m +1 – holds for m = 3k2 + 4k +1
Thus we have proved that the original statement holds.
7.Prove the statement by indirect proof: for a natural number a it holds: If a4 + 2 is not divisible by 3, then a is divisible by 3.
Solution:
B‘ => A‘:
If a is not divisible by 3, then a4 + 2 is divisible by 3
1)
a = 3k + 1
a4 +2 = (3k +1)4 +2
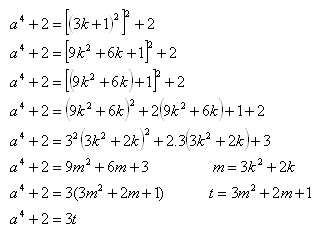
For a = 3k + 2, carry out the proof yourself.
The original statement holds.
8.Prove by contradiction the statement: For all positive real numbers a, b it holds that:
Proof:
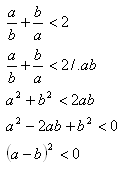
The negated statement does not hold for any positive real numbers. The original statement holds.
9.Prove by contradiction: The number √3 is irrational
Solution:
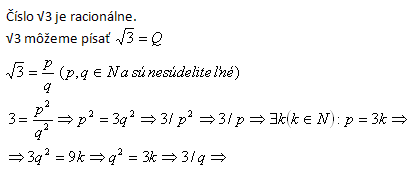
The number p is divisible by 3, the number q is divisible by 3, therefore they are not coprime. The assumption that √3 is a rational number does not hold. The original statement that √3 is irrational holds, as was to be shown.
10.Using mathematical induction, prove the statement: For all natural numbers n it holds that:
Solution:
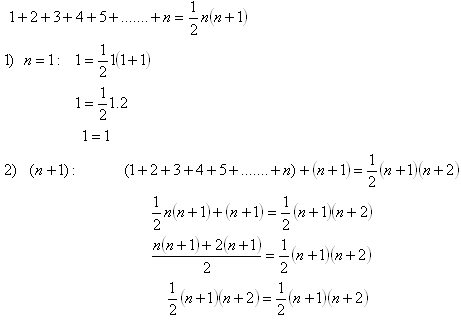
Thus we have proved the truth of the statement for all natural numbers n.
11.Using mathematical induction, prove the statement: For all natural numbers n it holds that:
Solution:
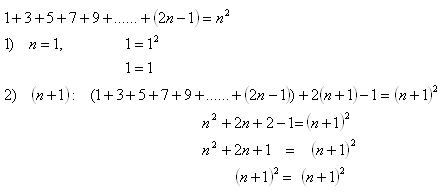
Thus we have proved the truth of the statement for all natural numbers n.
12.Using mathematical induction, prove the statement: For every natural number n it holds that:
Solution:
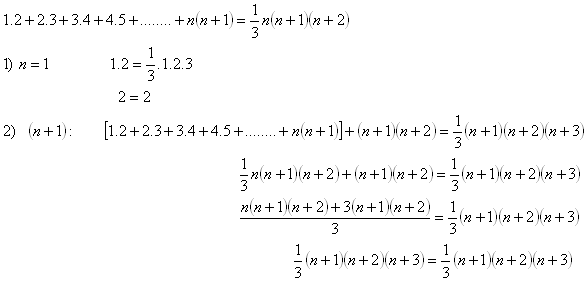
Thus we have proved the truth of the statement for all natural numbers n.
13. Using mathematical induction, prove the statement: For every natural number n it holds that:
Solution:
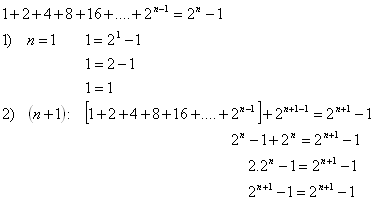
Thus we have proved the truth of the statement for all natural numbers n.
14.Using mathematical induction, prove the statement:
Solution:
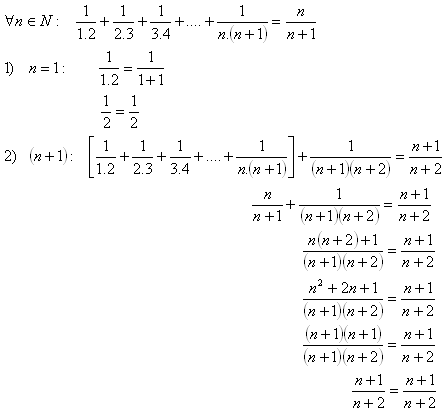
Thus we have proved the truth of the statement for all natural numbers n.
15.Using mathematical induction, prove the statement:
Solution:
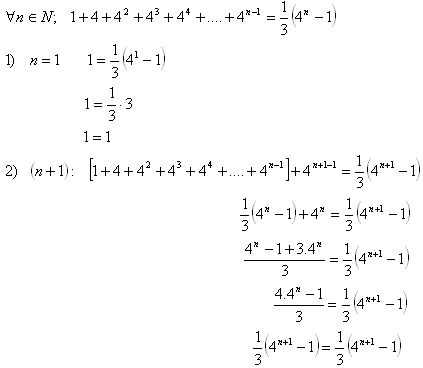
Thus we have proved the truth of the statement for all natural numbers n.
16.Using mathematical induction, prove de Moivre’s theorem
Solution:
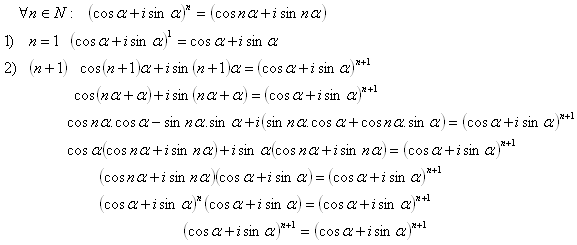
Thus we have proved the statement for all natural numbers.
17.Inside triangle ΔABC a point U is given. Prove that the following relation holds
Solution:
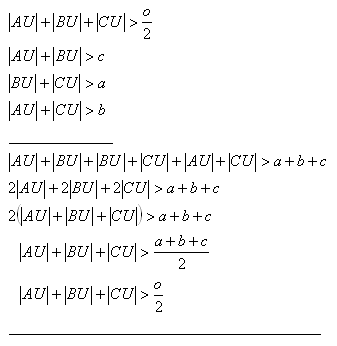
18.Prove the statement: A triangle’s median is less than half of the perimeter.
Solution:
In triangle ΔABC, |AB| = c, |AC| = b, |BC| = a. Point S is the midpoint of side a. |BS| = |SC| = a /2. The median to side a is ta = |AS|.
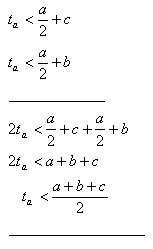
19.Prove the statement:
Solution:
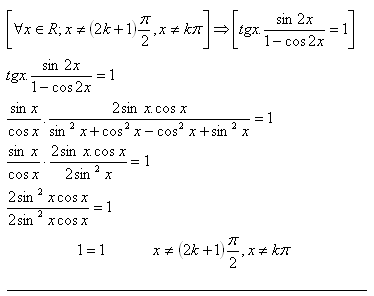
20.A sphere and a cone are inscribed in an equilateral cylinder. The base of the cone coincides with the base of the cylinder, the vertex of the cone is at the center of the other base. Show that Archimedes’ result holds. (Archimedes approx. 287–212 BC)
Solution: