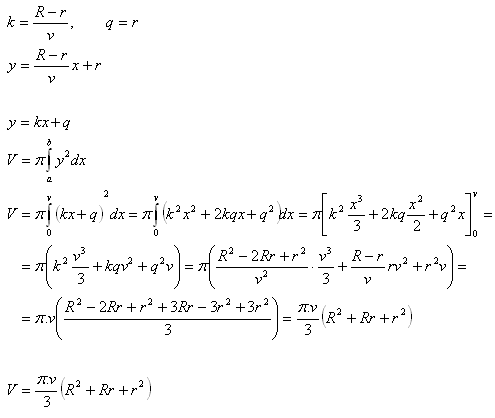Cubic volume
1.Explain the term Cubic volume – “cubature”!
Solution:
Cubic volume – Cubature is the calculation of the volume of solids of revolution. We compute the volume of a body formed by rotating a plane figure (a rectangle, triangle, trapezoid, circle, etc.) about the x-axis. The plane figure is bounded by the x-axis, the lines x1 = a, x2 = b, and the curve y = f(x).
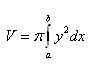
2.Derive the formula for the volume of a right circular cylinder with base radius r and height v.
Solution:
The solid is formed by rotating a rectangle about the x-axis. The rectangle is bounded by the x-axis and the lines x1=a=0, x2=b= v, y = r.
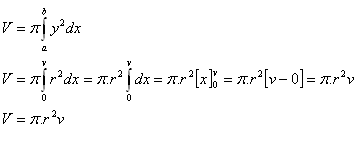
3. Derive the formula for the volume of a right circular cone whose base radius is r and height is v.
Solution:
4.Derive the formula for the volume of a sphere with radius r!
Solution:
The solid is formed by rotating the circle x2 + y2 = r2 about the x-axis.
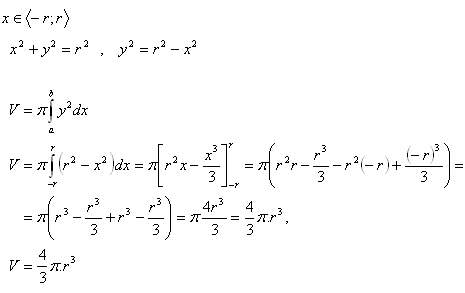
5.Derive the formula for the volume of a rotational ellipsoid with semi-axes a, b.
Solution:
The solid is formed by rotating an ellipse about the x-axis. The ellipse has the equation:
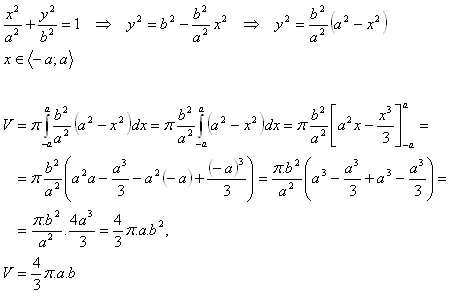
6.Derive the formula for the volume of a rotational paraboloid formed by rotating the parabola y2 = 2px about the x-axis. The paraboloid has height v.
Solution:
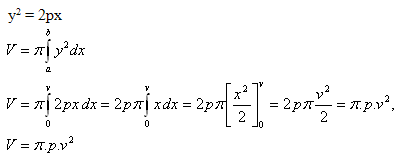
7.Compute the volume of the solid obtained by rotating the function y = cos x about the x-axis.
Solution:
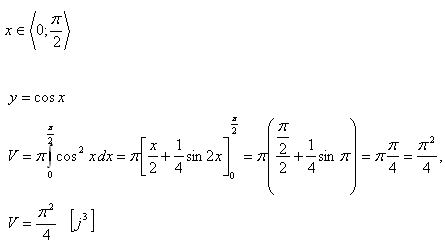
8. Derive the formula for the volume of a frustum of a cone. The lower base has radius R, the upper base r. The height of the cone is v.
Solution:
The solid is formed by rotating an isosceles trapezoid about the x-axis. The trapezoid is bounded by the x-axis, the two lines x1 = a = 0, x2 = b = v, and the line y = k.x + q, where the constants k and q denote