Determinant
1. What is a determinant and what properties does it have?
Solution:
The determinant of order n is a number D, created from n2 numbers aik, arranged into a square table with n rows and n columns of the form

a11,a12,...a1n => row of the determinant
a11,a21,...an1 => column of the determinant
a11,a22,...ann => main diagonal
Value of the determinant:
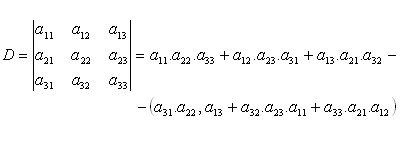
Determinant of degree n:
A determinant of degree n has n rows and n columns (n > 3). The subdeterminant (minor) Mij corresponding to the element aij is obtained from determinant D by removing the i-th row and j-th column.
Algebraic complement (cofactor):
Aij = (-1)i+j · aij · Mij
Expansion of a determinant:
a.) along the i-th row:
D = ai1Mi1 + ai2Mi2 + ... + ainMin
b.) along the j-th column:
D = a1jM1j + a2jM2j + ... + anjMnj
2. State the theorems about the value of a determinant.
Solution:
- 1) The value of the determinant does not change if we swap its rows with its columns (i.e., transpose).
- 2) The value of the determinant does not change if we add (or subtract) any multiple of another row to a given row.
- 3) The value of the determinant equals zero if all elements in some row are zero.
- 4) The value of the determinant equals zero if some row is a scalar multiple of another row.
- 5) The value of the determinant equals zero if two rows are identical.
- 6) The determinant changes sign if we interchange two rows of the determinant.
- 7) We can factor out a number “c” from the determinant that multiplies some row.
- 8) Multiplying the determinant by a number “c” means multiplying one of its rows by that number (only a single row). c <> 0
Note:
The stated properties also apply to the columns of the determinant.
3. Compute the determinants:
Solution:
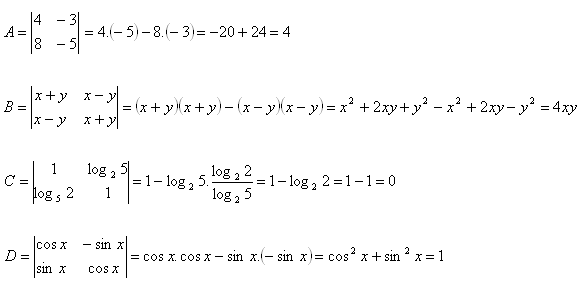
4. Compute the determinants:
Solution:
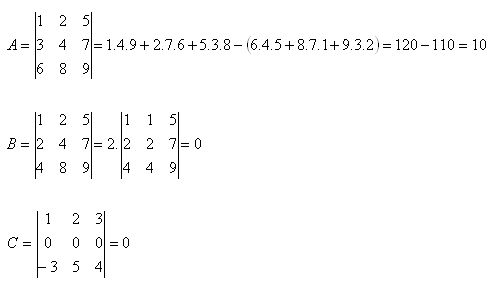
5. Compute the determinants:
Solution:
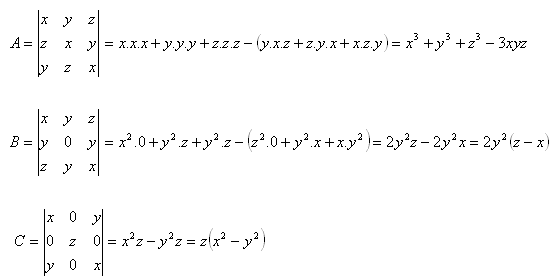
6. Solve the equations in R:
Solution:
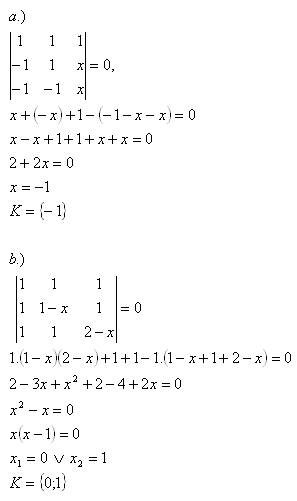
7. Solve the equations in R:
Solution:
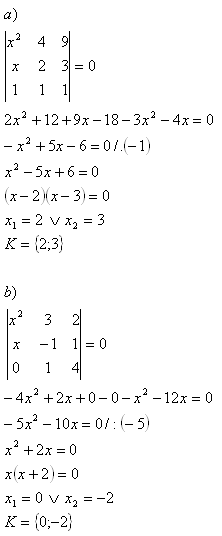
8. Calculate the area of triangle ABC with vertices:
A[3;2], B[6;3], C[4;7]
Solution:
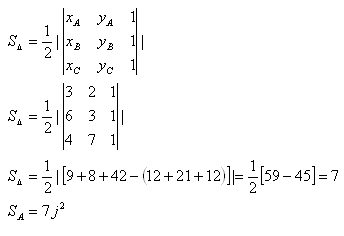
The area of triangle ABC is 7 j2
9. Calculate the area of triangle ABC whose sides have equations:
Solution:
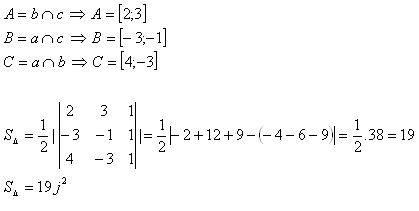
The area of triangle ABC is 19 j2
10. Determine whether points A, B, C lie on one line, if:
A[1;4], B[3;0], C[0;6]
Solution:
The condition for points A[xa;ya], B[xb;yb], C[xc;yc] to lie on the same line is
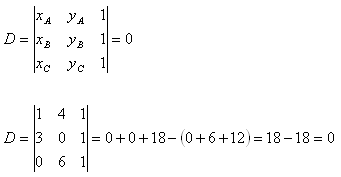
D = 0 => Points A, B, C lie on the same line
11. Determine whether points A, B, C lie on one line, if:
A[1;1], B[0;4], C[4;3]
Solution:
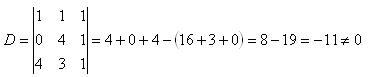
D <> 0 => The points do not lie on the same line
12. Given points A, B, C. Find the first coordinate of point B so that A, B, C lie on the same line. Given:
A[0;3], B[xB;-1], C[-3;9]
Solution:
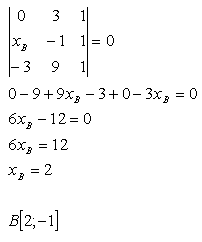
13. Write the equation of the line that passes through points A and B if:
A[3;2], B[0;4]
Solution:
Let points A[xa;ya], B[xb;yb], X[x,y] lie on line p, then
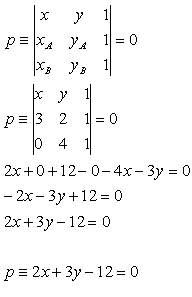
14. Write the equations of the sides of triangle ABC with vertices
A[4;2], B[7;3], C[1;6]
Solution:
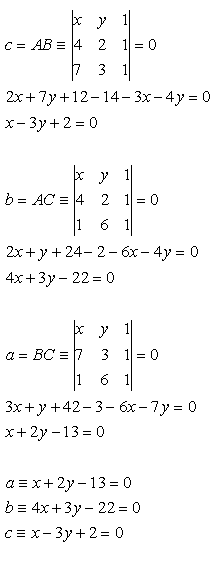
15. Compute the vector cross product of two vectors:
Solution:
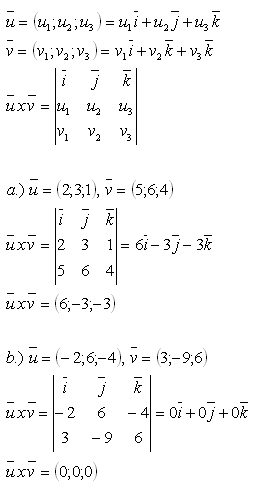
16. Solve the systems of linear equations:
Solution:
Cramer's rule 1.
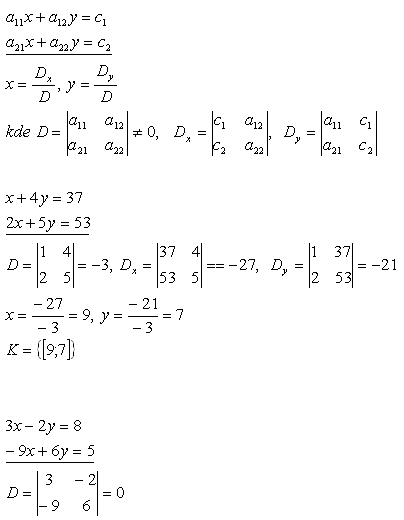
The system has no solution
17. Solve the system of linear equations:
Solution:
Cramer's rule 2.
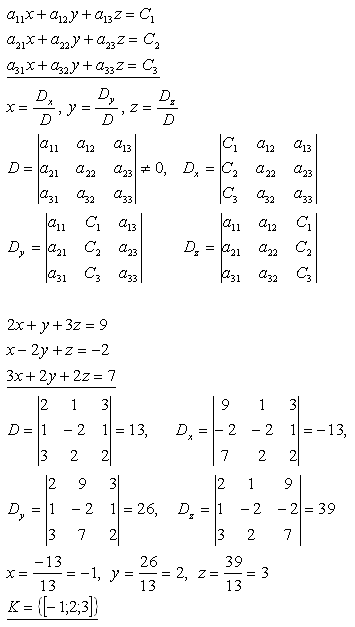
18. Solve the system of linear equations:
Solution:
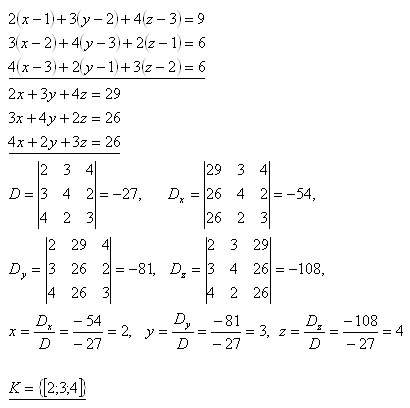
19. For the given determinant D determine the algebraic complement A23
Solution:
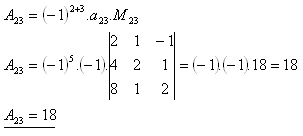
20. Compute the determinant:
Solution:
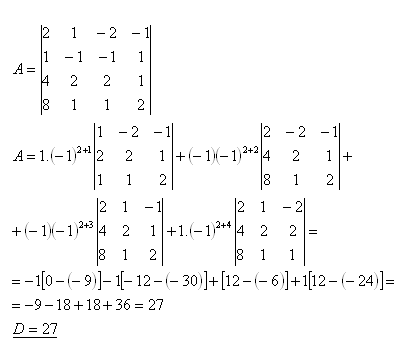
21. Compute the determinant:
Solution:
Expansion along the fourth row:
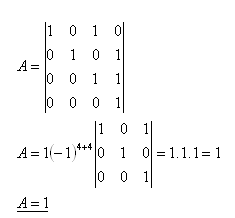
22. Determine whether points A, B, C, D lie in the same plane if:
A[2;2;-2], B[1;1;4], C[0;2;0], D[3;1;2]
Solution:
Condition:
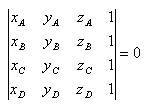
Solution:
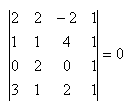
Expansion along the third row:
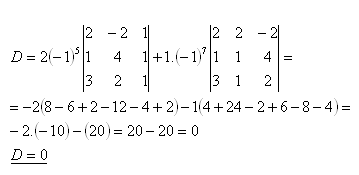
Points A, B, C, D lie in the same plane.
23. Write the general equation of the plane given by points A, B, C if:
A[0;0;5], B[-2;0;1], C[1;2;4]
Solution:
Equation of the plane:
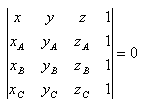
Solution:
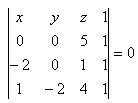
Expansion along the second row:
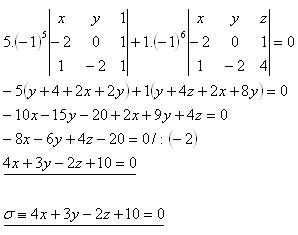
24. Write the general equation of the plane passing through points A, B, C if
A[2;1;2], B[1;-2;3], C[0;0;0]
Solution:
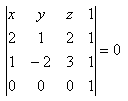
Expansion along the fourth row:
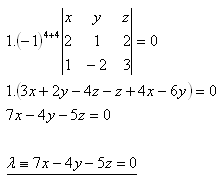
25. Solve the system of equations:
x + y + z + u = 10
x + y – z – u = 4
x – y + z – u = 2
x – y – z + u = 0
Solution:
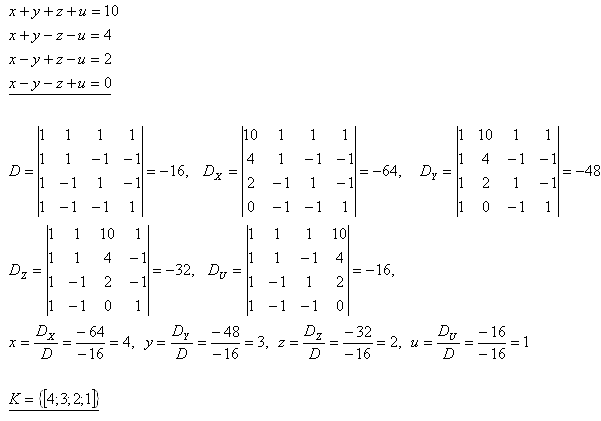
```