Point, line, and plane
1. Explain in which mutual positions the following can be:
a) a point and a plane
b) a line and a plane
Solution:
Point and plane.
Point A[a1; a2; a3] lies in plane ρ: a.x + by + cz + d = 0 if its coordinates satisfy the equation of plane ρ.
Point A[a1; a2; a3] does not lie in plane ρ: ax + by + cz + d = 0 if its coordinates do not satisfy the equation of plane ρ.
The distance of point A[a1; a2; a3] from plane ρ: ax + by + cz + d = 0 is given by:
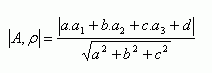
Line and plane.

2. Which of the points A [3;2;7], B[0;2;1], C[-8;-2;-1] lie in plane τ : 2x – 3y – 2z + 8 = 0. What must the value of x be so that point M[x;-6;2] also lies in the given plane?
Solution:
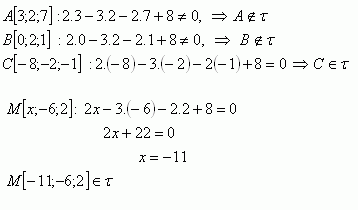
The points C [-8;-2;-1] and M [-11;-6;2] lie in plane τ.
3. Determine whether point A[9;-2;0] lies in plane ξ: 3x + 2y – 6z + 26 = 0. If it does not lie in it, calculate its distance from the given plane.
Solution:
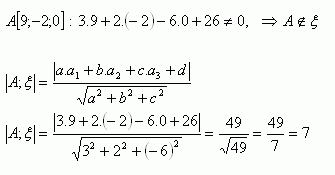
Point A does not lie in plane ξ. Its distance from this plane is 7 units.
4. Calculate the distance from the origin of the coordinate system to the plane:
Solution:
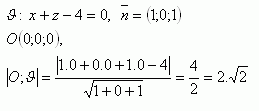
The distance from the origin of the coordinate system to plane υ is approximately 2.828 units.
5. Determine the mutual position of planes ρ and τ. If they are parallel and distinct, also find their distance. The equations of the planes are:
Solution:
Planes ρ and τ are parallel but distinct.
Determination of the distance between the planes.
In plane ρ we find any point A and determine its distance from plane τ. Point A: choose x = 1, z = 0, 11.1 - 2y - z.0 + 15 = 0 , 2y = 26, y = 13 → A[1; 13; 0]:
The planes are parallel but distinct. Their mutual distance is 4 units.
6. What must hold for the y-coordinate of point A [1;y;0] so that its distance from plane τ: 3x – 2y – 6z = 0 is 5 units?
Solution:
The points that satisfy the conditions are A[1;-16;0] and A*[1;19;0]
7. Determine the mutual position and the intersection point of the line and the plane, if they are not parallel.
Plane:
τ: x + y + z + 1
Line:
Solution:
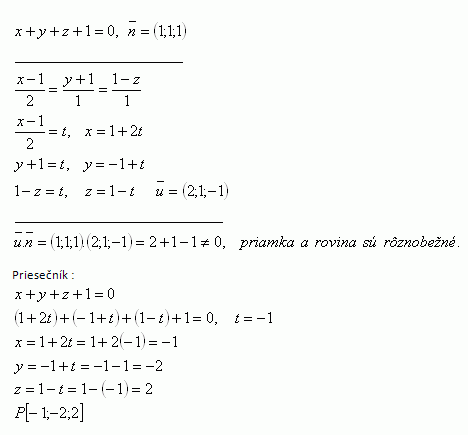
The line intersects the plane at point P [-1; -2; 2].
8. Given is line p and plane ρ. Find their common point and the angle between the line and the plane. Their equations are:
Solution:
Intersection of the line with the plane: Angle between the line and the plane:
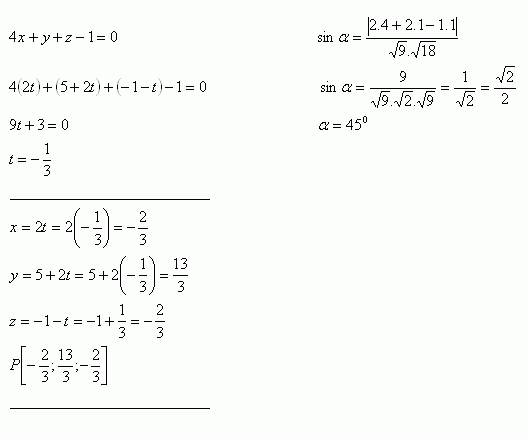
9. Determine the mutual position of planes ρ and π, whose equations are:
Solution:

10. Calculate the angle between two non-parallel planes:
Solution:
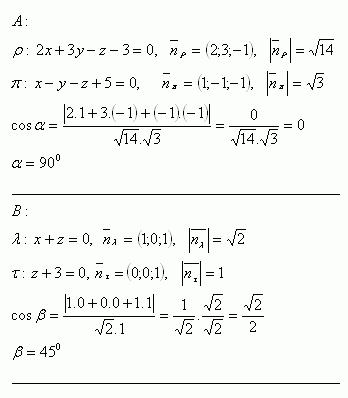
11. Determine the common point of line p and plane τ if:
Solution:
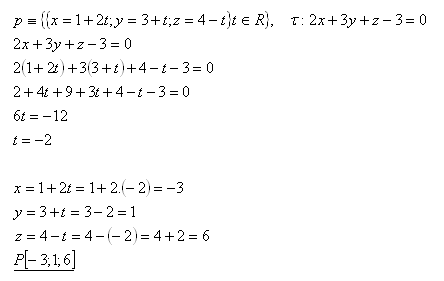
The common point of line p and plane τ is P[-3; 1; 6].
12.The distance of point A from plane σ represents the side of square ABCD. Calculate the area of this square if:
Solution:
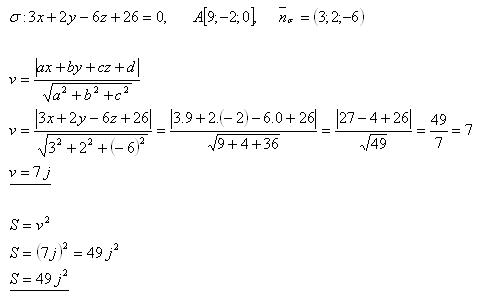
The area of square ABCD is S = 49 j2.
13. Calculate the distance of two parallel planes σ and τ if:
Solution:
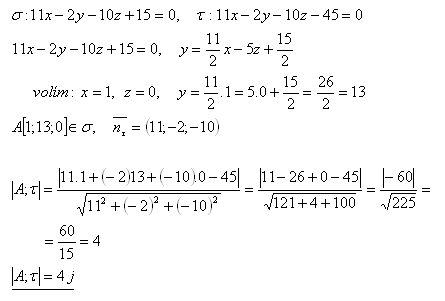
The distance of the two parallel planes σ and τ is 4 j.
14. Calculate the length of the altitude drawn from vertex V in tetrahedron ABCV, if:
Solution:
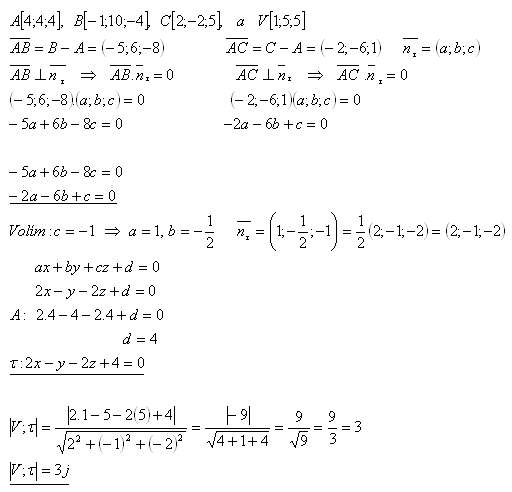
The altitude of tetrahedron ABCV is 3 units.
15. Determine real numbers a, b so that planes π and τ are parallel, given that:
Solution:
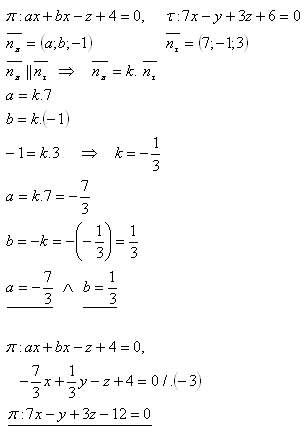
16. Determine the mutual position of planes σ and η if:
Solution:
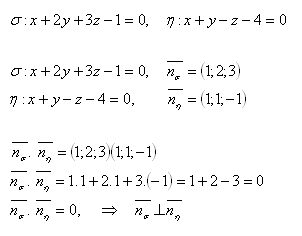
Planes σ and η are perpendicular to each other.
17. Show that the coordinate planes xy and yz are perpendicular to each other.
Solution:
Coordinate plane xy = ρ
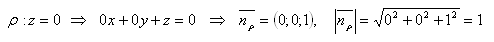
Coordinate plane yz = λ
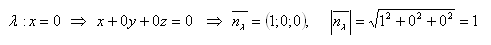
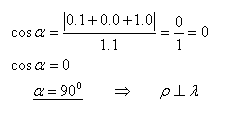
The coordinate planes xy and yz are perpendicular to each other.
18. Determine the angle between line p and plane μ if:
Solution:
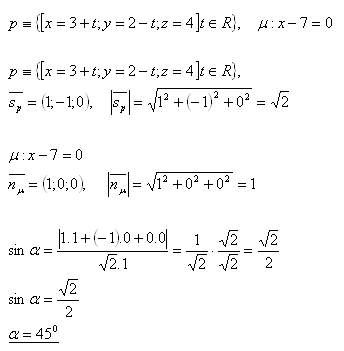
The angle between line p and plane μ is α = 450.
19.The vertices of the tetrahedron are points A, B, C, D. Determine the angle between edge AD and plane ρ = ABC if:
Solution:
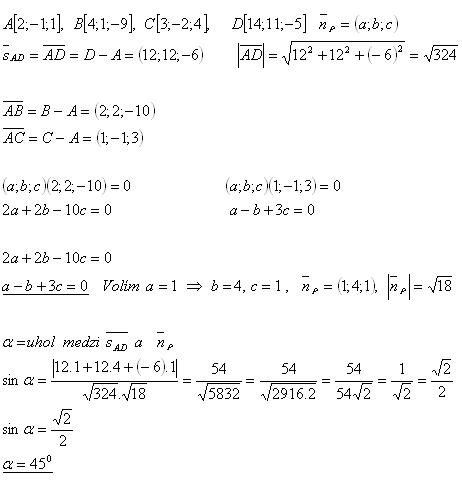
The angle between edge AD and plane ρ is α = 450.
20. Determine the mutual position of three planes if:
Solution:
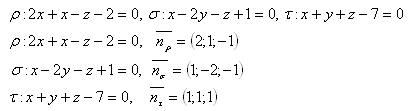
The normal vectors of the given planes are independent. The planes are not parallel.
Intersection of the planes P [x; y; z]:
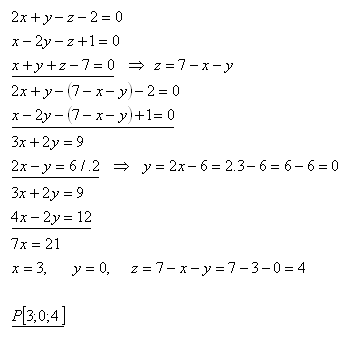
The planes ρ, σ, τ are non-parallel. They intersect at point P[3; 0; 4].