Behavior of a function
1. How do we determine the behavior of a function?
Solution:
a.) The function y = f(x) is increasing at point x0 if f‘(x0) > 0
b.) The function y = f(x) is decreasing at point x0 if f‘(x0) < 0
c.) The function y = f(x) has a stationary point at x0 if f‘(x0) = 0
d.) The function y = f(x) is convex at x0 if f‘‘(x0) > 0
e.) The function y = f(x) is concave at x0 if f‘‘(x0) < 0
f.) The function y = f(x) has an inflection point at x0 if f‘‘(x0) = 0 ^ f‘‘(x0) ≠ 0
g.) The function y = f(x) has a local minimum at x0 if f‘ (x0) = 0 ^ f‘‘ (x0) > 0
h.) The function y = f(x) has a local maximum at x0 if f‘ (x0) = 0 ^ f‘‘ (x0) < 0
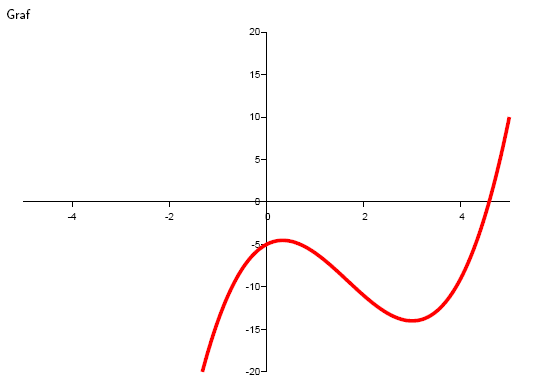
2. Given the function y = x3 – 5x2 + 3x - 5. Determine for which x the function is increasing, decreasing, convex, and concave.
Solution:
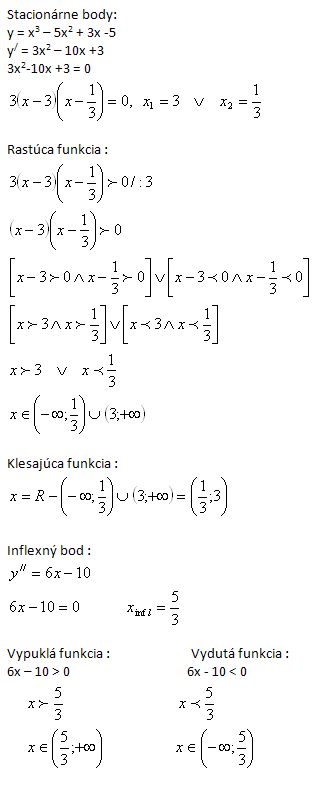
3.Check whether the function y = x3 -5x2 +3x -5 is decreasing and convex at x0 = 2.
Solution:
y = x3 -5x2 +3x -5
y‘ = 3x2 -10x +3
y‘(2) = 3·22 -10·2 +3
y‘(2) = -5 < 0
The function is decreasing.
y‘ = 3x2 -10x +3
y‘‘ = 6x - 10
y‘‘(2) = 6·2 – 10
y‘‘(2) = 2 > 0
The function is convex.

4.Check whether the function is increasing and concave in the neighborhood of x0 = 0.
Solution:
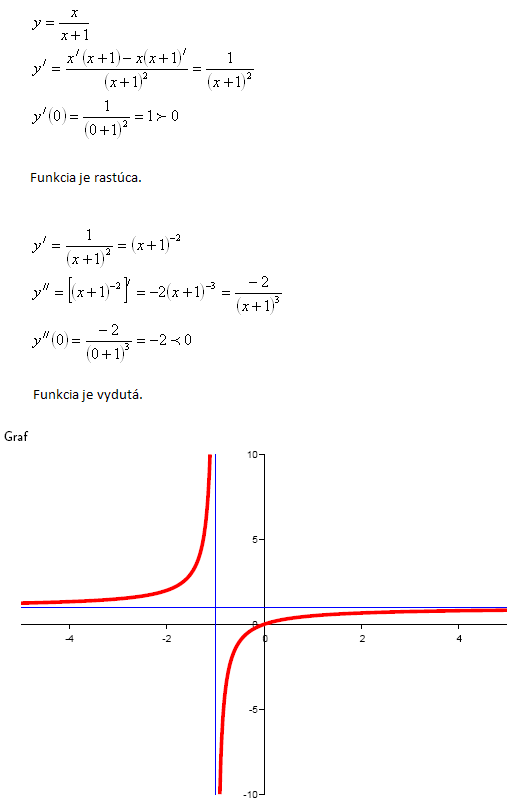
5. Given the function y = 2x2 – ln x. Determine for which x the function is decreasing.
Solution:

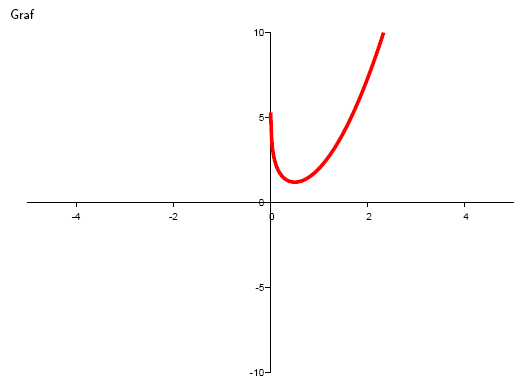
6. Determine the local extrema of the function y = x2(4 – x )2
Solution:
Local extrema:
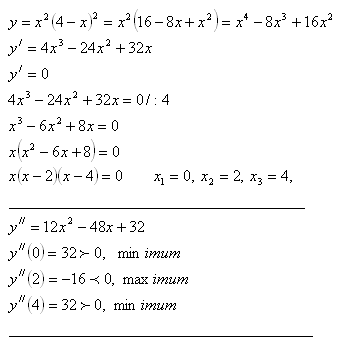
The function has a local minimum at x1 = 0 and x3 = 4, and a maximum at x2 = 2.
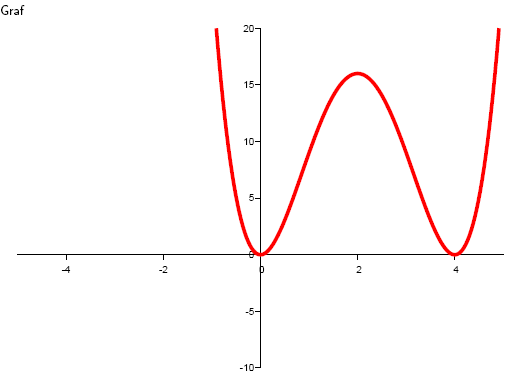
7. Determine the local extrema of the function y = sin x · (1+cos x)
Solution:
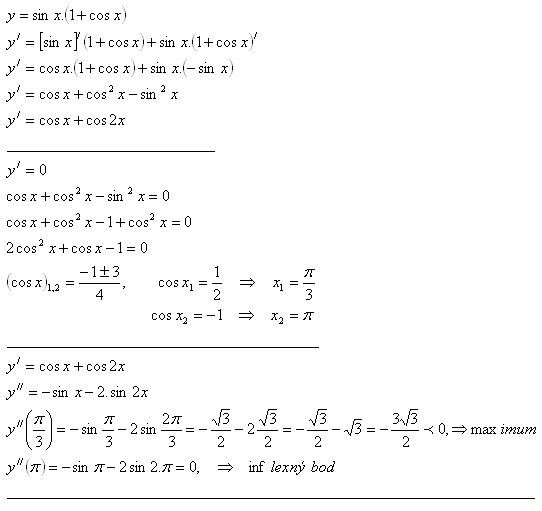
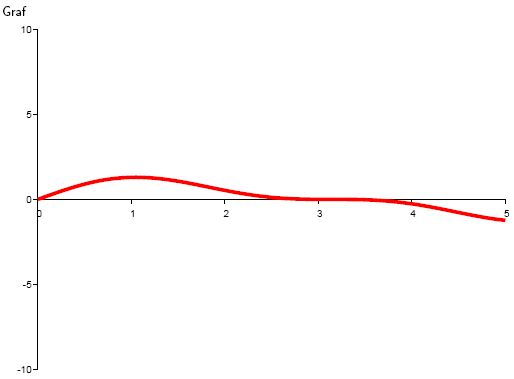
8.Find the stationary points and the intervals of increase and decrease of the function
Solution:

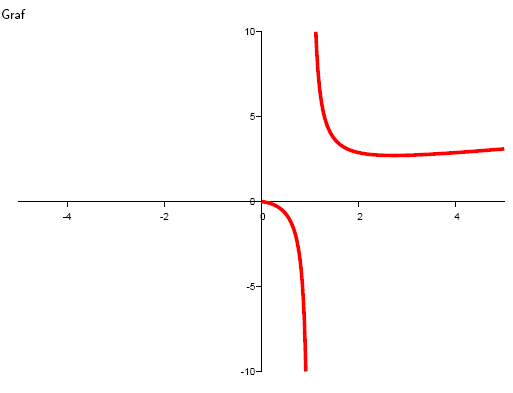
9.For which values of a, b is the point I[1; 3] an inflection point of the function y = ax3 + bx2 ?
Solution:
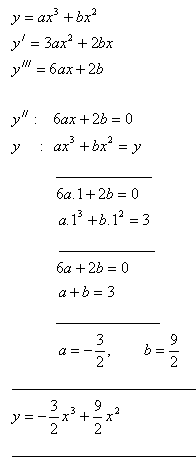
10. Find the local extrema of the function
Solution: