Mechanical work
1. Characterize mechanical work
Solution:
For a force to do mechanical work, it must move the body; it must act on the body along a path.
The force acting on the body can be
- a.) parallel to the displacement
- b.) not parallel to the displacement
Mechanical work is the product of the force and the distance the body travels under the action of the force.
a.) W = F·s
b.) W = F·s·cosα, where α is the angle between F and s
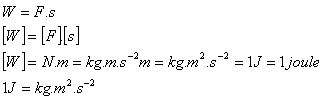
No work is done if:
- 1.) F = 0
- 2.) s = 0
- 3.) α = 90o, cos90o= 0, the force is perpendicular to the displacement
2.Determine the work that must be done to move a crate of mass 400 kg over a distance of 20 m along a horizontal floor with uniform motion
- b.) if the coefficient of friction between the floor and the crate is f = 0.15
Solution:
a.) W = Fg · s
W = m·g·s
W = 400 kg·10 m·s-2·20 m = 80 000 J = 80 kJ
b.) W = ( Fg + Ft )·s = ( m·g + f·m·g )·s = s·m·g·(1+f )
W = 20 m·400 kg·10 m·s-2(1+0.15) = 92 000 J = 92 kJ
W = 92
In the first case we must do 80 kJ of work, in the second 92 kJ.
3.A worker loaded 4 m3 of sand onto a truck. With each shovel he took an average volume of 3 dm3 of sand and threw it to a height of 2.4 m. The average density of sand is ρ = 2600 kg·m-3. How much work did he do?
Solution:
V = 4 m3, V0 = 3 dm3 = 0.003 m3, h = 2.4 m, ρ = 2600 kg·m-3
Number of shovels: n = V : V0 = 4 m3 : 0.003 m3 = 1333 shovels
W = m·g·h·n
W = ρ·V0·g·h·n
W = 2600 kg·m-3·0.003 m3·10 m·s-2·2.4 m·1333 = 249 537.6 kg·m2·s-2 = 250·103 J
W = 250 kJ
The worker did about 250 kJ of work.
4.Calculate the work done if 7 blocks, each 8 cm high and with a mass of 12 kg, lying on the ground were stacked on top of each other. What work is done if the blocks lying on the ground were stacked like this on scaffolding at a height of 1 m?
Solution:
Analysis:
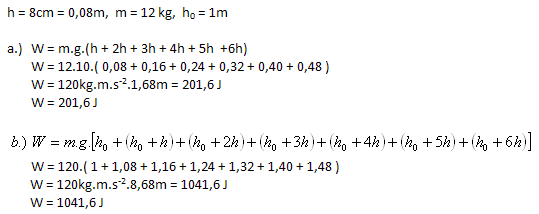
In the first case the work done is 201.6 J, in the second the work is 1041.6 J.
5. A car with a mass of 2000 kg moved with uniform rectilinear motion along a road with an 8% incline. How much work did the car’s engine do over a path of 1.5 km? (Neglect friction and all resistive forces.)
Solution:
Analysis:
m = 2000 kg, s = 1.5 km = 1500 m, sin α = 0.08
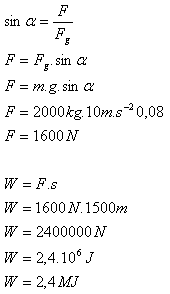
The car’s engine did 2.4 MJ of work.
6.A tractor with a load of mass 6 tons reached a speed of 18 km·h-1 in 12 s under uniformly accelerated motion on a horizontal road. How much work did it do?
Solution:
Analysis:
m = 6 t = 6000 kg, t = 12 s, v = 18 km·h-1 = 5 m·s-1, W = ?
The tractor did work W = 75 kJ.
7.By what distance does a body move if a force of 152 N acting at an angle of 51o does work of 5.14 kJ?
Solution:
Analysis:
F = 152 N, α = 51o, W = 5.14 kJ = 5140 J, s = ?
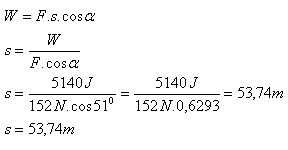
The body moves by 53.74 m.
8.A body acted on by a force of 500 N moved 25 m. At what angle did the force act if the work done was 12 kJ?
Solution:
Analysis:
F = 500 N, s = 25 m, W = 12 kJ = 12 000 J, α = ?
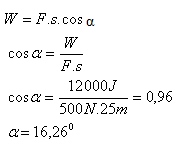
The force acted at an angle α = 16.26o.
9.A boy pulls a sled with a load of total mass 60 kg along a horizontal road (f = 0.1) with a force of 75 N over a path of 30 m. Determine:
- a.) the acceleration of the sled with the load
- b.) the speed of the sled at the end of the path
- c.) the work the boy did
Solution:
Analysis:
m = 60 kg, F = 75 N, s = 30 m, f = 0.1
- a.) Acceleration of the sled with the load
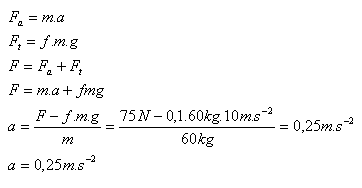
- b.) Speed of the sled at the end of the path
W = F·s
W = 75 N·30 m = 2250 J
The acceleration of the sled is a = 0.25 m·s-2, its speed at the end of the path is v = 3.875 m·s-1. The work the boy did is W = 2250 N.
10. A freight train with a mass of 600 t left the station and after 5 minutes of uniformly accelerated motion on a horizontal track (f = 0.01) reached a speed of 54 km·h-1. How much work did the locomotive’s tractive force do?
Solution:
Analysis:
m = 600 t = 6·105 kg, t = 5 min = 300 s, v = 54 km·h-1 = 15 m·s-1, f = 0.01, W = ?
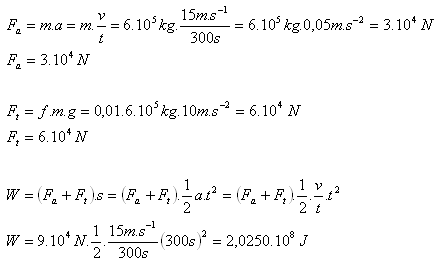
The locomotive’s tractive force does work W = 202.5 MJ.