Matrix
1. What are the basic properties of matrices.
Solution:
A rectangular scheme of m, n real numbers arranged into m rows and n columns is called a matrix (of type m,n). If m = n, it is a square matrix of degree n. The numbers a11, a32, ... amn are called elements of the matrix.
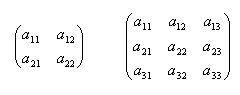
Zero matrix: Identity matrix:
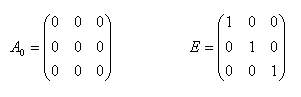
Inverse matrix A–1:
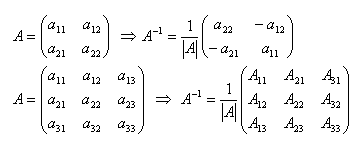
Sum of matrices A + B
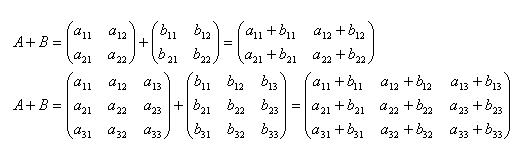
2. Explain the procedure for multiplying two matrices.
Solution:
The product of two matrices only makes sense if the left matrix has as many columns as the right matrix has rows. Such matrices are called “conformable.”
The product of matrices is not commutative!
Multiplication of a matrix by a number:
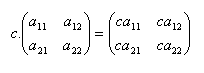
Product of matrices A.B
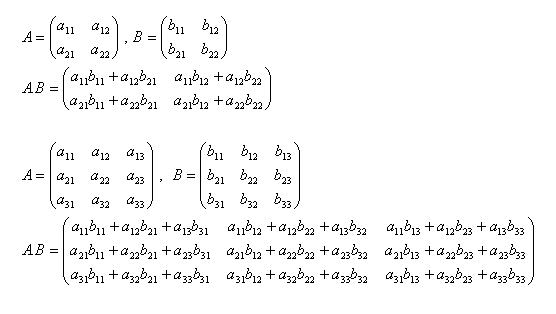
3.Add matrices A+B and M+N if
Solution:
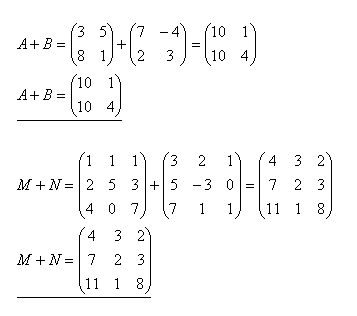
4.Multiply matrices A.B and C.D if
Solution:
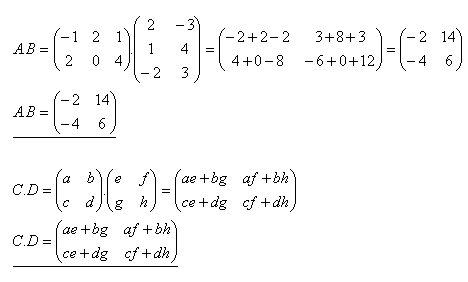
5.Show that the product of matrices is not commutative.
Solution:
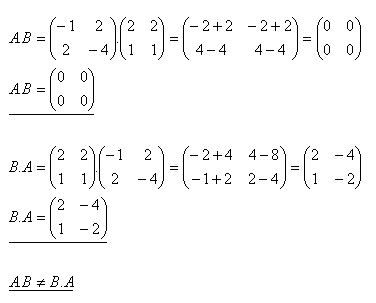
6.Given matrix A. Find the matrix A2 if
Solution:
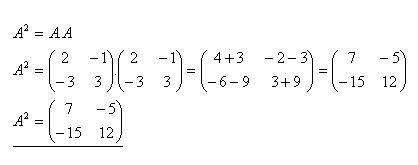
7.Given matrix B. Find the matrix B2 if
Solution:
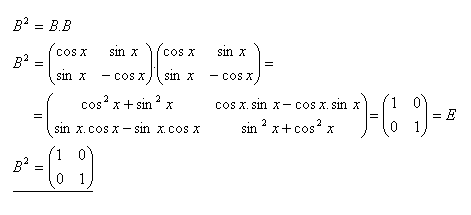
8.Find the product of matrices A.B if
Solution:
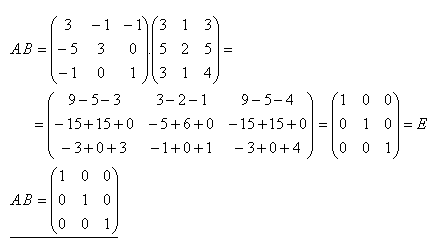
9.Explain the procedure for calculating the inverse matrix A–1 from matrix A.
Solution:
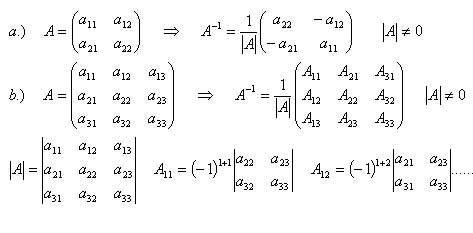
In the check, the inverse matrix must be multiplied from the left.
For the product of matrices, the commutative law does not hold.
10.For matrix A, find the inverse matrix A–1 and check if
Solution:
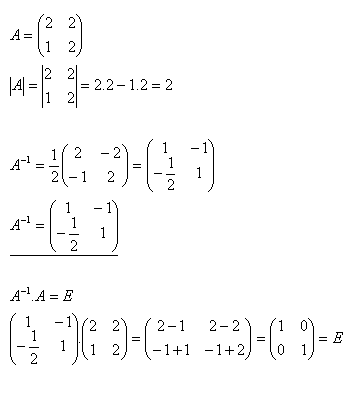
11.For matrix A, find the inverse matrix A–1 and check if
Solution:
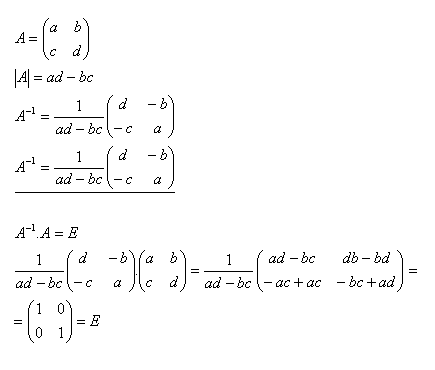
12.Calculate the inverse matrix A–1 for matrix A, if
Solution:
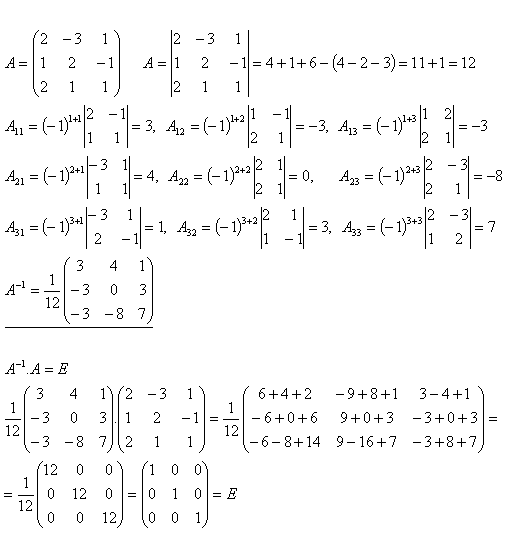
13.Calculate the inverse matrix A–1 for matrix A and check (see example 12), if
Solution:
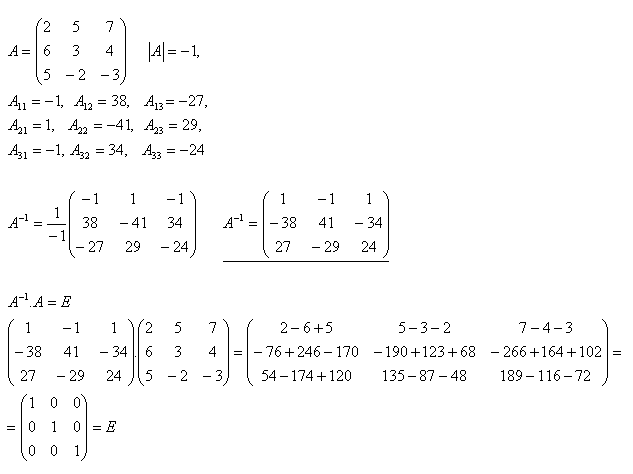
14.Solve the matrix equation A + X = B if
Solution:
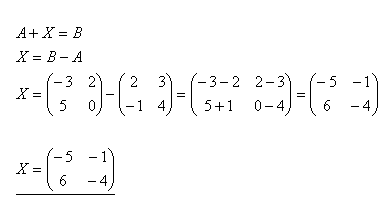
15.Calculate matrix X from the equation 2A + 3X = B if
Solution:
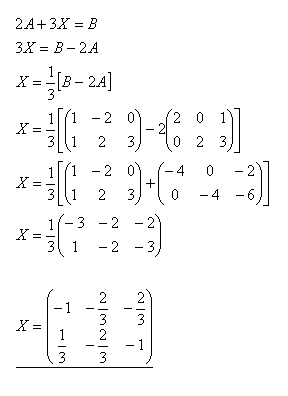
16.Solve the matrix equation A.X = B and check if
Solution:
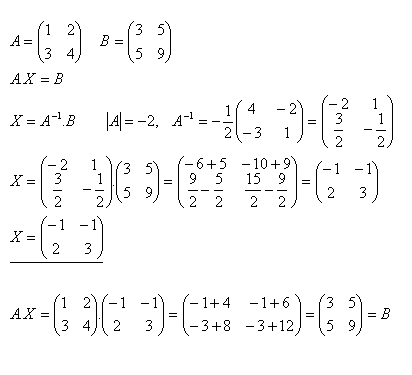
17.Solve the equation A.X = B and check if
Solution:
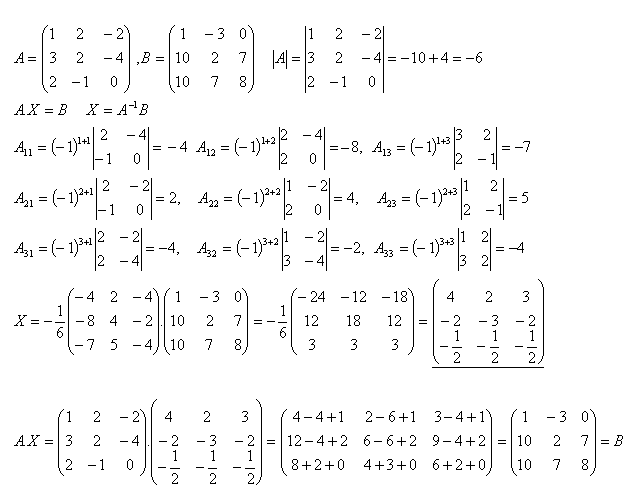
18.Explain the procedure for solving a system of linear equations using the inverse matrix.
Solution:
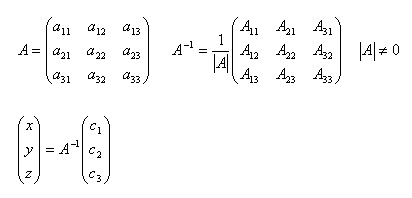
19.Using the inverse matrix, solve the system of equations:
Solution:
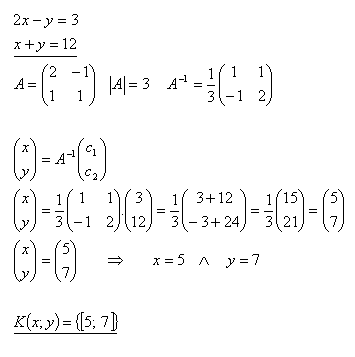
20.Using the inverse matrix, solve the system of equations:
Solution:
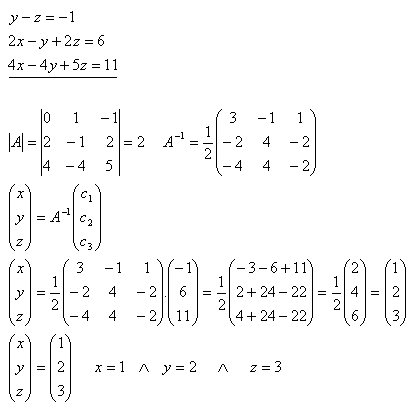
21.Using the inverse matrix, solve the system of equations:
Solution:
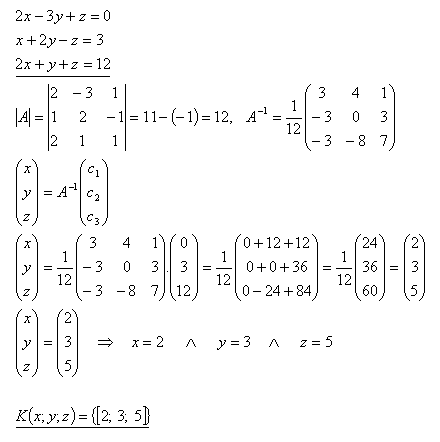
22.Using the inverse matrix, solve the system of equations:
Solution:
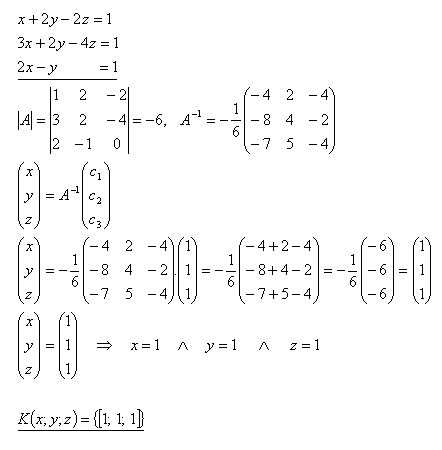
23.Explain the concept of the “rank of a matrix” and the conditions for solving a system of linear equations by the Gauss method.
Solution:
The rank of a matrix h is the number that gives the maximum number of linearly independent rows of the matrix. The rank of a matrix does not change if:
- a.) we swap the order of its rows
- b.) we multiply any row by a nonzero number
- c.) we add another row to any row
- d.) we add a linear combination of other rows to any row
- e.) we remove a row that is a linear combination of other rows
- f.) we remove a zero row
- g.) we exchange rows for columns (the “transposed matrix” is formed)
The stated properties of matrix rank also hold for columns.
Frobenius theorem:
A system of linear equations has a solution only if the rank of the coefficient matrix h equals the rank of its augmented matrix h/.
h = h/
a.) h = h/ and h = n unique solution
b.) h = h/ and h < n infinitely many solutions (where n is the number of unknowns in the system)
24.Solve the system of equations by the Gauss method:
Solution:
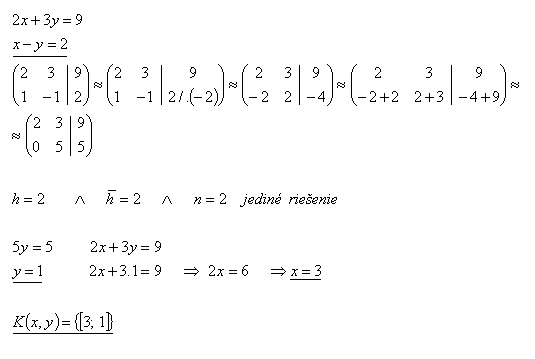
25.Solve the system of equations by the Gauss method:
Solution:
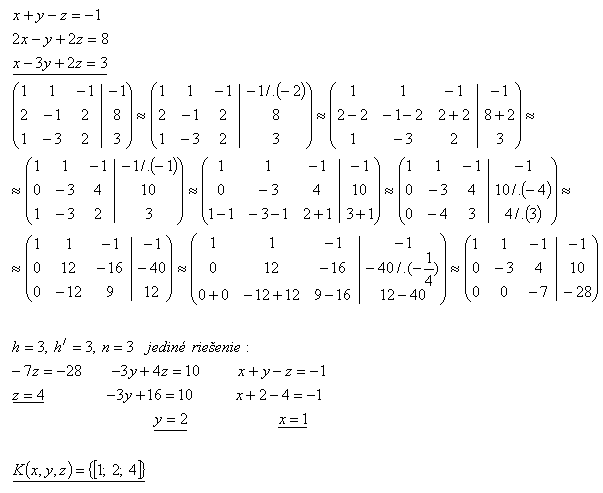
26.Solve the system of linear equations using the Gauss method:
x + 2y + 3z = 0
2x – y + z = 3
3x + y – z = 5
Solution:
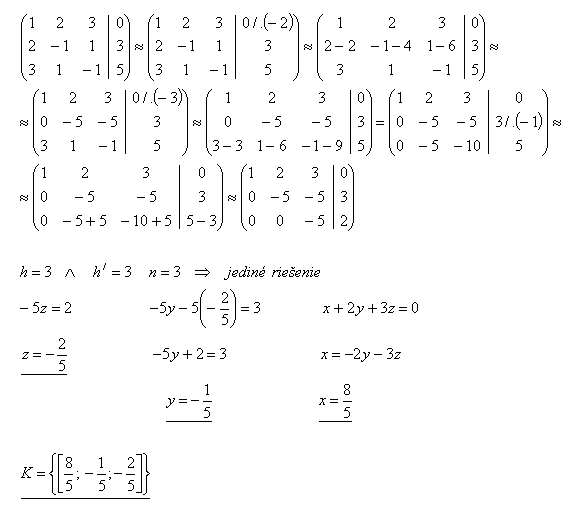
27.Solve the system of equations by the Gauss method:
Solution:
