Atomic packaging
1. What does an atom look like?
Solution:
Aristotle (384 BC): Matter is continuous, it can be divided infinitely. Leucippus, Democritus (5th century BC): Matter is discontinuous, composed of indivisible particles – atoms. J.J. Thomson (1856–1940) created the so-called “plum pudding model”. The atom is a positively charged sphere in which electrons float. E. Rutherford (1871–1937) created the “planetary model of the atom”. The entire mass of the atom (as well as its positive charge) is concentrated in the nucleus (10–15m). Around the nucleus, electrons orbit in circles (ellipses – A. Sommerfeld). The radius of the atom is about 10–10m. The main shortcoming of this model was that when orbiting the nucleus, the electron would lose energy, its speed would decrease, it would spiral inward and fall into the nucleus. The material world could not exist. N. Bohr (1883–1962) created the “quantum model of the atom”.
- a.) An electron can move around the nucleus only along specific circular paths called orbitals (energy levels). The length of an orbital equals an integer multiple of the wavelength of the de Broglie wave corresponding to the electron.
- b.) If the electron moves along an orbital, it does not emit energy
- c.) When the electron transitions from one orbital where it had energy En to another orbital with lower energy Em, it emits one light quantum – a photon. K. Heisenberg (1901–1976), E. Schrödinger (1887–1961) created the “quantum mechanical, probabilistic model”. It is not possible to determine both the position and velocity of an electron with equal precision. One can determine regions where the electron may be found with a certain probability around the nucleus.
2. What properties does the hydrogen atom have in Bohr's model?
Solution:

3. How long does it take light to pass through an atom with a radius r = 3.10–10m?
Solution:
Analysis:
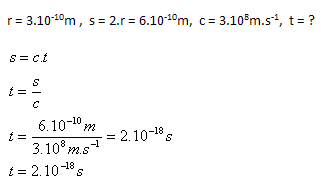
Light passes through the atom in t = 2.10–18s.
4. Calculate the ground state energy of the hydrogen atom E1. 1J = 0.6242.1019 eV
Solution:

The ground state energy of the hydrogen atom is E1 = –13.6eV.
5. Calculate the energies of the hydrogen atom in stationary orbits with principal quantum number n = 1,2,3,4,5,6. The energy of the first orbit is E1 = –13.6 eV. (Example 4)
Solution:
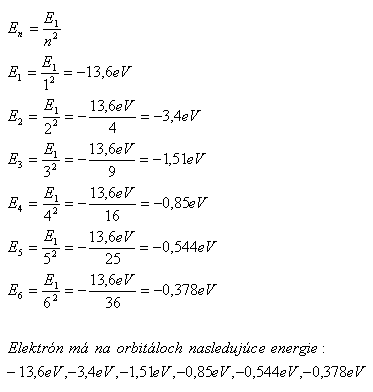
An electron has the following energy in its orbitals
6. Calculate the velocities of the electron on individual orbitals in the hydrogen atom, knowing that
r1 = 0.53.10–10m.
Solution:
Analysis:
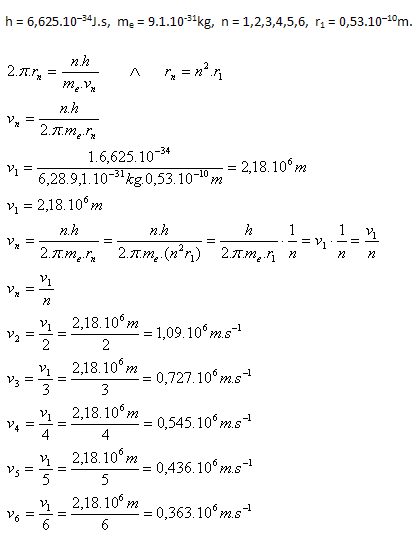
7. Determine the frequency of the visible lines of the Balmer series (J. Balmer, 1825–1898) for hydrogen. The series arises from electron transitions to the second orbit.
Solution:
Analysis:
E1 = –13.6eV, E2 = –3.4eV, E3 = –1.5eV,
E4 = –0.85eV, E5 = –0.544eV, E6 = –0.378eV
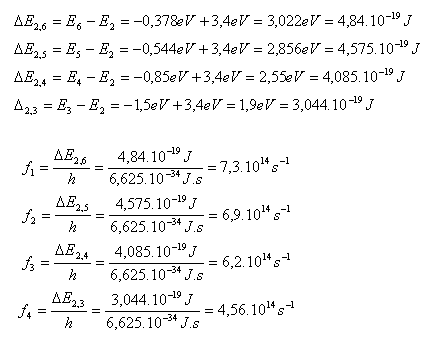
8. A hydrogen atom in the ground state absorbed energy of 10.2eV. To which energy level did the electron transition?
Solution:
Analysis:
ΔE = 10.2eV, E1 = –13.6eV, n = ?
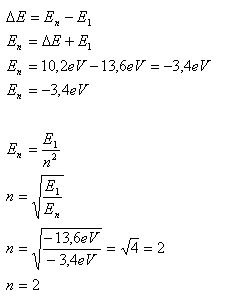
The electron transitioned to the second energy level.
9. A helium–neon laser has power of 2mW and emits radiation with wavelength 632.8nm. Determine the energy, mass and momentum of the emitted photons.
Solution:
Analysis:
P = 2.10–3W, λ = 632.8.10–9m, E = ?, m = ?, p = ?
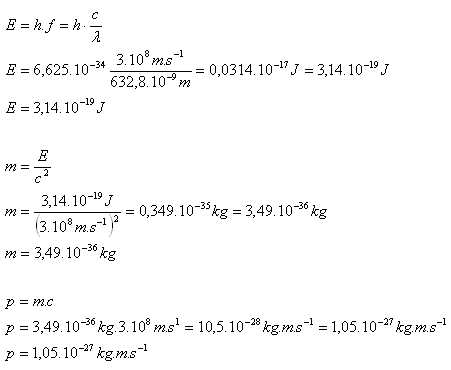
A photon has energy E = 3.14.10–18J, mass m = 3.49.10–36kg and momentum p = 1.05.10–27kg·m·s–1.
10. The hydrogen atom transitions from stationary state n = 6 to state m = 1. Calculate the frequency and wavelength of the emitted photon. Use the Rydberg formula. (J.R. Rydberg 1854–1919)
Solution:
Analysis:
n = 6, m = 1, R = 3.29.1015s–1
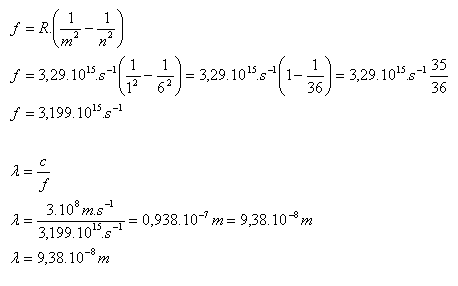
The emitted photon has frequency f = 3.199.1015 Hz and wavelength λ = 9.38.10–8m.
11. Calculate the amount of electromagnetic energy emitted by a hydrogen atom if its electron jumps from the first orbital to an infinitely distant orbital.
Solution:
Analysis:
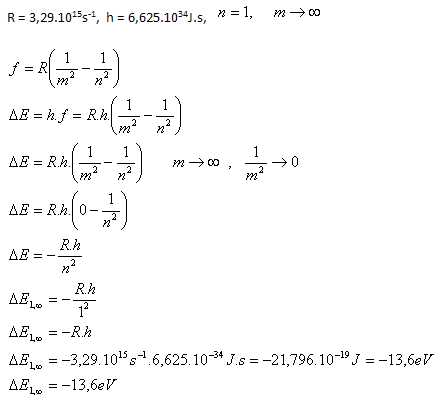
The hydrogen atom emits –13.6eV of electromagnetic energy.
12. Derive the Rydberg constant R
Solution:
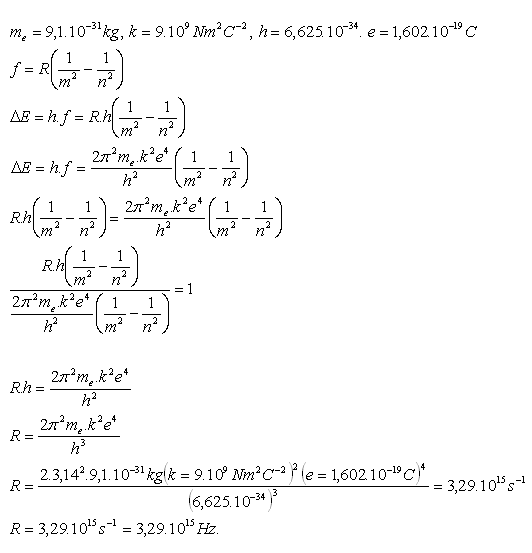
13.Determine the three longest wavelengths of the Balmer series. This series corresponds to the emission of energy by an electron when transitioning 3 – 2, 4 – 2, 5 – 2.
Solution:

The longest wavelengths of the Balmer series correspond to the colors red, blue and violet.
14.What voltage must be present in an electric field if we want to accelerate an electron in it so that during a collision with a hydrogen atom it can excite the atom from the ground state to the first excited state?
Solution:
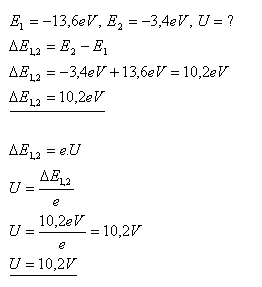
The voltage in the electric field must be U = 10.2 V.
15.The radius of the first circular orbit of the electron in the hydrogen atom is r = 0.53×10–10 m. Determine the intensity of the electric field from the nucleus on this orbit.
Solution:
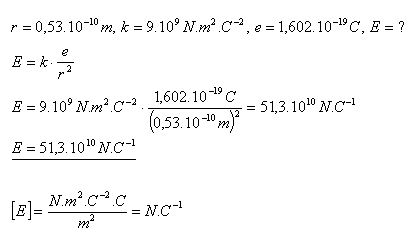
The electric field intensity on the first orbit of the electron in the hydrogen atom is E = 51.3×1010 N·C–1.
16.What is the potential of the atomic nucleus on the first electron orbit in the hydrogen atom?
(E = 51.3×1010 N·C–1 – example 15)
Solution:
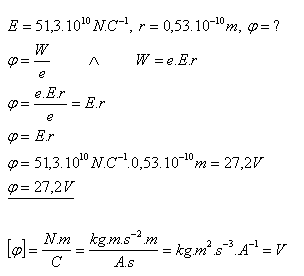
The potential on the first electron orbit in the hydrogen atom is φ = 27.2 V.
17.Determine whether the photoelectric effect can occur when visible light strikes zinc. WV(Zn) = 4 eV. The shortest wavelength of visible light is λ = 390 nm.
Solution:
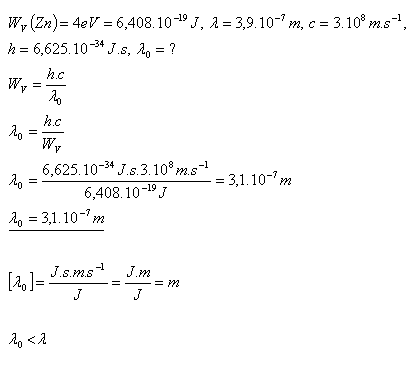
Photoemission will not occur because λ0 < λ.
18.The work function of platinum is WV(Pt) = 5.29 eV. Calculate the threshold frequency f0 at which the photoelectric effect occurs.
Solution:
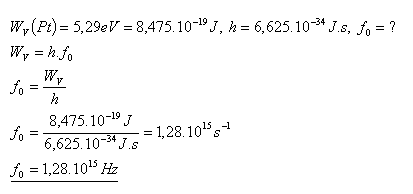
The threshold frequency at which the photoelectric effect occurs is f0 = 1.28×1015 Hz.
19.What is the speed of electrons emitted from the surface of cesium if it is illuminated with monochromatic light of wavelength λ = 590 nm? The work function of cesium is WV(Cs) = 1.93 eV.
Solution:
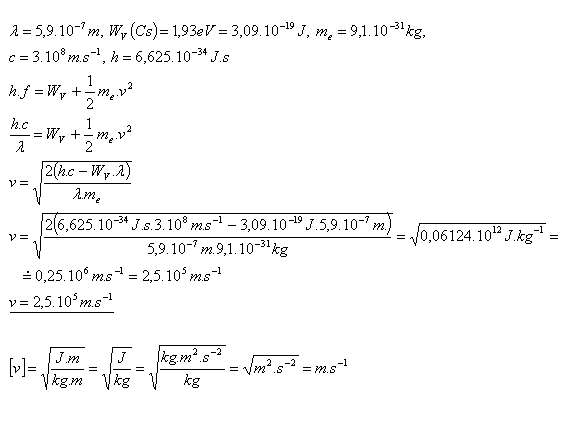
The electrons leave the surface of cesium with a speed v = 2.5×105 m·s–1.
20.Derive the relation for calculating the energy of an electron that is confined to a segment of length L.
Solution:
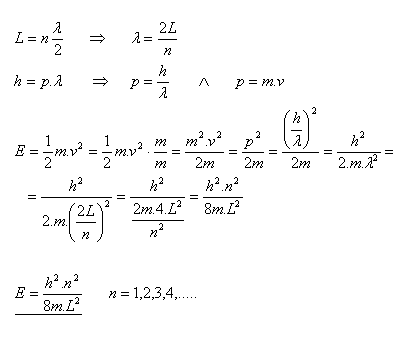
21.What will be the energy of the ground and first excited state of an electron confined to a segment of length L = 4×10–10 m?
Solution:
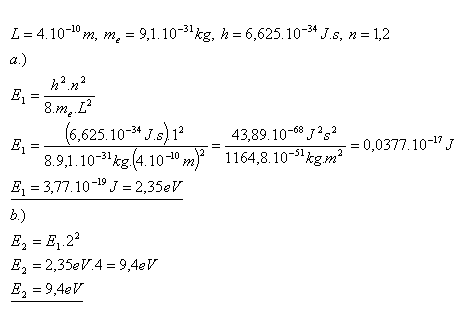
The electron energies are E1 = 2.35 eV, E2 = 9.4 eV.
22.What must be the length of the segment to which an electron is confined so that the difference between the ground state and the first excited state is less than 3 eV?
Solution:
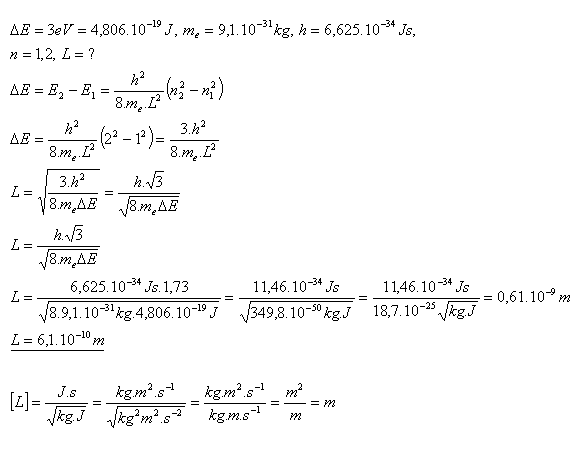
The length of the segment must be approximately L = 6×10–10 m.
23.What is the electron configuration of sodium, iron, copper, and silver? Use the table in example no. 2.
Solution:
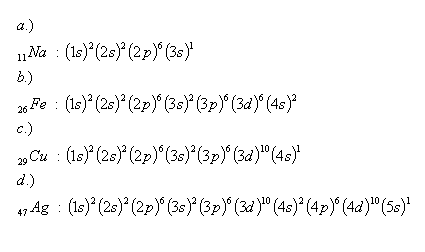
24. Which elements have the following configurations:
Solution:
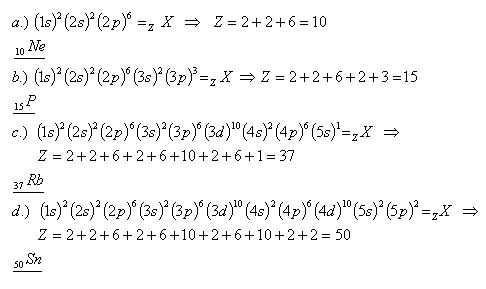
These are the elements neon, phosphorus, rubidium and tin.
25.Determine the energy of the electron in the ground state of the butadiene molecule with configuration (1s)2(2s)2. The electrons move along the entire length L = 0.6×10–9 m of the molecule.
Solution:
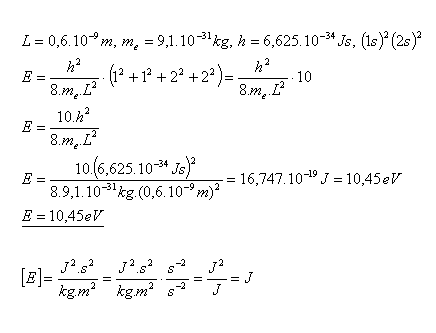
The energy of the electron in the ground state of the butadiene molecule is E = 10.45 eV.