Arithmetic Progression
1.Characterize an aritmetic progression:
A progression (a2)∞n+1 is told to be „arithmetic“ if and only if exists such d є R real number, so that for all n є N stands an+1 = an + d
Number d is called arithmetic progression difference.
For an arithmetic progression stands:
- an = a1 + (n-1)d
- ar = as + (r-s)d
- s = a1 + a2 + a3 + ... + an =
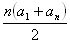
- If d > 0 the progression is increasing
- If d < 0 the progression is decreasing
- If d = 0 the progression is constant
2.Find out whether the following progression is arithmetic:
Solution:
a1 = -2, a2 = -1, a3 = 0, a4 = 1, a5 = 2 etc.
The progression is arithmetic; difference d = 1.
3.Enumerate first 6 progression members of an arithmetic progression that fits following conditions:
a1 + a4 + a6 = 71
a5 – a2 – a3 = 2
Solution:
a1 + a1 +3d +a1 +5d = 71
a1 + 4d – a1-d –a1 -2d = 2
3a1 + 8d = 71
-a1 + d =2/3
3a1 + 8d = 71
-3a1 + 3d = 6
a1 – d = -2
a1 = d - 2
a1 = 7 - 2
a1 = 5
11d = 77
d = 7
(a2)n-16 = 5;12;19;26;33;40
4.Enumerate first 6 progression members of an arithmetic progression that fits following conditions:
Solution:
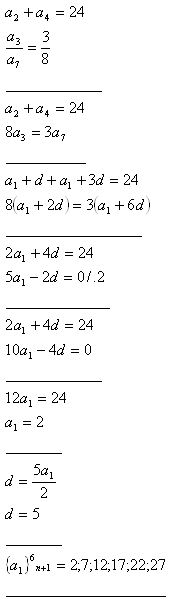
5.An aritmetic progression consists of 8 numbers. Sum of the middle members is 41, sum of the first and the last member is 114. Enumerate the progression members.
Solution:

6.Insert 4 numbers between the roots of the quadratic equation x2 – 16x +39 = 0 so that they will make an arithmetic progression.
Solution:
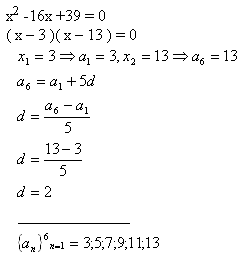
Numbers to insert: 5;7;9;11
7.The lengths of the sides of a right triangle make an arithmetic progression. The longer cathetus is 24 cm long. Find out the perimeter of the triangle.
Solution:
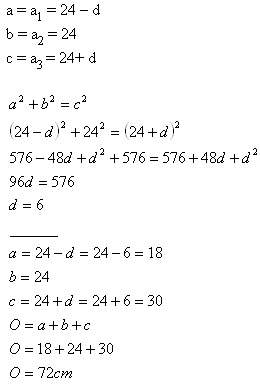
The perimeter of the triangle equals 72 cm.
8.Find out the sum of integers 1+2+3+4+5+6+7+.............+100.
Solution:
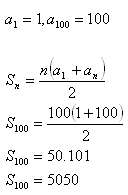
Sum of the numbers S = 5050.
9.Iron pipes are stored in 8 rows. The top row contains of 13 pipes, next row always contains of one more pipe than the previous one. How many pipes are there?
Solution:
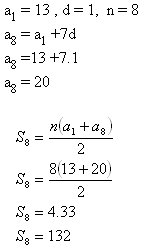
There are 132 pipes.
10.The angles in a triangle make an arithmetic progression. The smallest angle is 20°. Determine sizes of the other angles.
Solution:
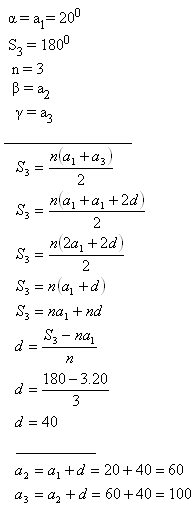
The angles are 20°, 60° and 100°.
11.Sizes of the sides of a cuboid make 3 members of an arithmetic progression. Sum of the sizes equals 24 cm, the volume of the cuboid equals 312 cm3. Determine the sizes of the sides.
Solution:
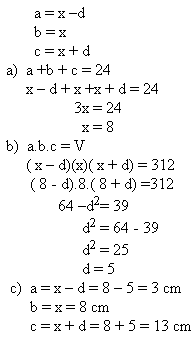
The sizes of the sides are 3 cm, 8 cm and 13cm.
12.How long would a rock be falling to a mine somewhere in South America which is deep 2500 m if it moves 4,904 m in the first second and extra 9,808 m for every next second?
Solution:
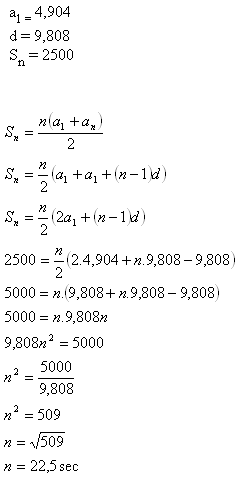
The rock would fall for approximately 22,5 sec.