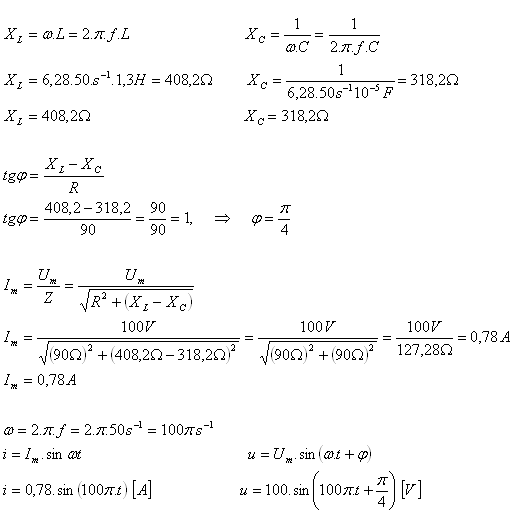AC Circuits
1. Characterize alternating electric current and alternating current circuits.
Solution:
Alternating electric current (AC) is a time-varying, periodically changing electric current. Both the magnitude and the direction of the current change. Alternating current is generated based on the law of electromagnetic induction: if a conductor (coil) rotates in a homogeneous magnetic field, an alternating voltage and an alternating current are induced in the conductor.
Alternating current circuits:
1) Circuit with Resistance (Resistor) R
The instantaneous current and voltage are in phase.
Resistive reactance:
2) Circuit with Inductance (Coil) L
The current lags behind the voltage.
Inductive reactance:
3) Circuit with Capacitance (Capacitor) C
The current leads the voltage.
Capacitive reactance:
4) RLC, RL, RC, LC Circuits in Series
Impedance:
RLC:
RL:
RC:
LC:
Condition: At resonance,
2.An alternating voltage with frequency f = 50 Hz has amplitude Um = 200 V. Write the equation for the alternating voltage. Find the instantaneous value of the voltage at time t = 4 ms.
Solution:
Analysis:
Um = 200 V, f = 50 Hz, t = 4 ms, u = ?
u = Um·sin(ωt)
u = Um·sin(2·π·f·t)
u = 200 V·sin(2·π·50·t)
u = 200·sin(100·π·t)
u = 200 V·sin(100·π·50·s-1·4·10-3s) = 200 V·sin(72°)
u = 200 V·0.951 = 190.2 V
u = 190.2 V
The equation of the alternating voltage is u = 200·sin(100·π·t).
The instantaneous value of the voltage at time t = 4 ms is u = 190.2 V.
3.The alternating current in an electrical circuit is described by the equation i = 5·sin(200·π·t) [A]. Determine the current amplitude, the frequency and the period of the current. Also determine the instantaneous value of the current at time t = 1.25·10–3 s.
Solution:
i = 5·sin(200·π·t) [A]
i = Im·sin(ω·t)
Im = 5 A,
ω·t = 200·π·t, 2·π·f = 200·π, 2·f = 200 s-1, f = 100 Hz
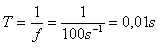
i = 5·sin(200·π·t) [A]
i = 5·sin(200·π·1.25·10-3 s) [A]
i = 5·sin(45°) = 5·0.707 A = 3.54 A
i = 3.54 A
Im = 5 A, f = 100 Hz, T = 0.01 s, i = 3.54 A.
4.Determine the reactance of a coil with inductance 500 mH in an AC circuit with frequency 50 Hz. Calculate the current amplitude if the voltage amplitude is 314 V.
Solution:
Analysis:
L = 500·10-3 H, f = 50 s-1, Um = 314 V, XL = ?, Im = ?
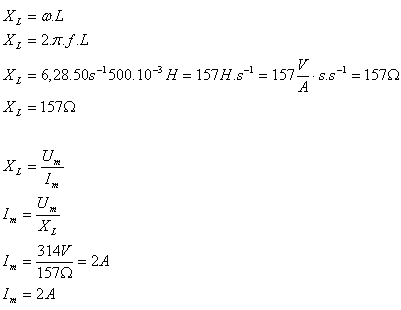
The inductive reactance of the coil is XL = 157 Ω, the current amplitude is Im = 2 A.
5. Determine the reactance of a capacitor with capacitance 20 μF in an AC circuit with frequency 50 Hz. Also calculate the voltage amplitude if the current amplitude is 2 A.
Solution:
Analysis:
C = 20 μF = 20·10-6 F, f = 50 s-1, Im = 2 A, XC = ?, Um = ?
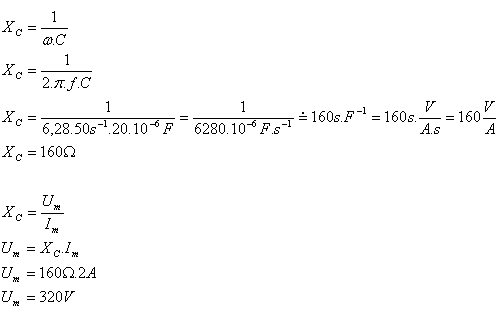
The capacitive reactance is XC = 160 Ω, the voltage amplitude is Um = 320 V.
6.An inductor with inductance 2 H and winding resistance 20 Ω is first connected to a DC voltage source of 20 V and then to an AC voltage source with the same RMS value and frequency 50 Hz. Determine the current in the circuit in both cases.
Solution:
Analysis:
L = 2 H, R = 20 Ω, U = 20 V, f = 50 s-1, I1 = ?, I2 = ?
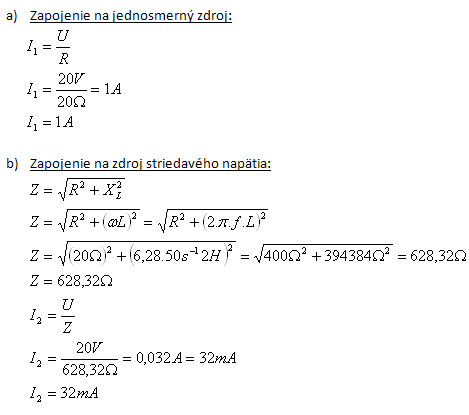
- a) When the inductor is connected to the DC source, the current through it is I1 = 1 A,
- b) when connected to the AC source the current is I2 = 32 mA.
7. An AC circuit with RMS voltage 200 V and frequency 50 Hz is connected to a series circuit formed by a capacitor with capacitance 16 μF and a resistor with resistance 150 Ω. Determine the impedance of the circuit, the current in the circuit, and the voltages across the capacitor and the resistor.
Solution:
Analysis:
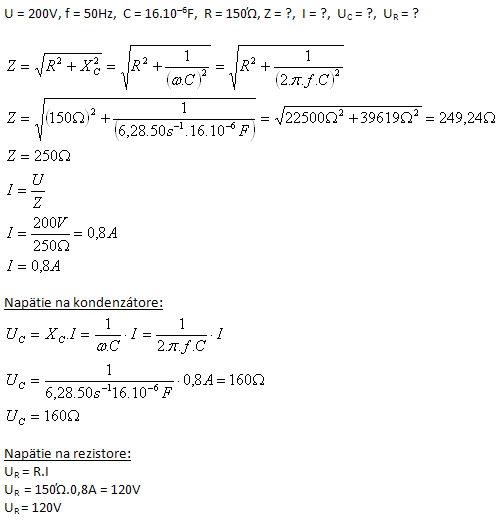
- Voltage on the capacitor
- Voltage on the resistor
The impedance of the circuit is Z = 250 Ω, the current in the circuit is I = 0.8 A, the voltage on the capacitor is UC = 160 V, and on the resistor UR = 120 V.
8.An oscillatory circuit consists of a coil with inductance 0.1 mH and a capacitor with capacitance 100 pF. Determine the resonance frequency.
Solution:
Analysis:
L = 0.1 mH = 10-4 H, C = 10-10 F, f = ?
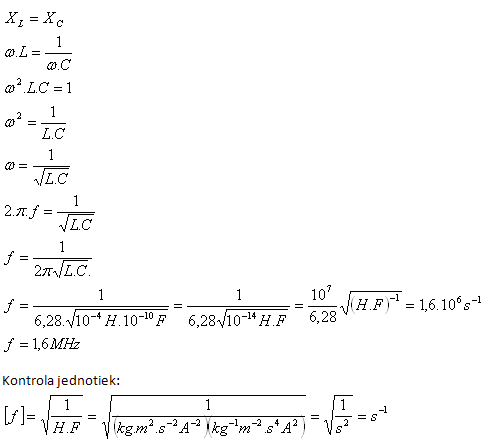
The resonance frequency is f = 1.6 MHz.
9.A coil with L = 5·10–2 H, whose winding has resistance R = 10 Ω, is connected in series with a capacitor C = 2·10–6 F. An alternating current with amplitude Im = 0.1 A and f = 500 Hz flows through the circuit. Determine the impedance Z of the circuit and the voltage amplitude Um.
Solution:
Analysis:
L = 5·10-2 H, R = 10 Ω, C = 2·10-6 F, Im = 0.1 A f = 500 Hz, Z = ?, Um = ?
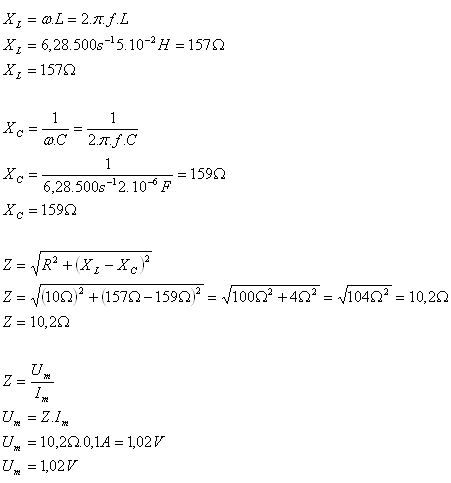
The impedance of the circuit is Z = 10.2 Ω, the voltage amplitude is Um = 1.02 V.
10. A series AC circuit consists of a resistor with R = 90 Ω, a coil with inductance L = 1.3 H, and a capacitor with capacitance C = 10–5 F. The circuit is connected to an AC voltage source with amplitude Um = 100 V and frequency f = 50 Hz. Write the equations for the instantaneous values of voltage and current in the circuit.
Solution:
Analysis:
R = 90 Ω, L = 1.3 H, C = 10-5 F, Um = 100 V, f = 50 Hz