Internal energy

1. What is the internal energy of a system and how can it be changed?

Solution:

A thermodynamic system is a collection of microscopic and macroscopic objects forming a whole that can exchange energy with each other or with the surroundings. The total energy of the system is the sum of the total kinetic energy of the disordered motion of particles and the total potential energy of the mutual positions of those particles.

U = E_k + E_P

First law of thermodynamics:

The change of the internal energy of the system ΔU equals the sum of the work W done on the system by surrounding bodies acting with forces and the heat Q delivered to the system by the surroundings.

ΔU = W + Q

a.) The system receives energy (work, heat): W > 0, Q > 0
b.) The system gives off energy (work, heat): W < 0, Q < 0

Change of internal energy caused by external work: (Q = 0)

\Delta U = E_p = m \cdot g \cdot h

\Delta U = E_k = \frac{1}{2} m v^2

Change of internal energy by heat exchange: (W = 0)

Heat capacity:

C = \frac{Q}{\Delta t} \quad [C] = J \cdot K^{-1}

Specific heat capacity (tables):

c = \frac{C}{m} = \frac{Q}{m \cdot \Delta t} \quad [c] = J \cdot kg^{-1} \cdot K^{-1}

Amount of heat received (or given) by a system:

Q = m \cdot c \cdot (t_2 - t_1) \quad [Q] = J

Calorimetric equation (mixing rule):

m_1 c_1 (t - t_1) = m_2 c_2 (t_2 - t) \quad t_1 < t < t_2

With calorimeter:

m_1 c_1 (t - t_1) + C (t - t_1) = m_2 c_2 (t_2 - t)

2.English physicist J. P. Joule (1818 – 1889) attempted to determine the specific heat capacity of water. In his experiment he used two weights, each of mass 14 kg, and let them fall 12 times in a row from a height of 2 m into a container with water. The container held water of mass 6.7 kg. During the experiment the temperature of the water increased by 0.24 K. What value of the specific heat capacity of water did he find?

Solution:

Analysis:

2.m₁ = 28 kg, E_p =2.m₁.g.h = 28kg.10m.s^-2.2m = 560 J,

E_k = 12.E_p = 12.560J = 6720 J, m₂ = 6,7kg, Δt = 0,24 K

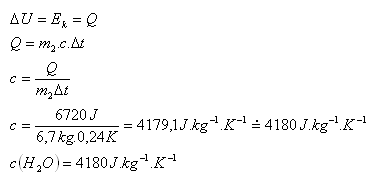
Specific heat capacity of water c(H₂O) = 4180 J·kg^-1·K^-1

3.Think about a short test: If T(K) = t(°C) + 273.15, then which of the statements is true?

Temperature 0^oC is

A) –100^oK B) 0^oK C) 273.15 K

2) Temperature -273.15 is

A) the freezing temperature of helium B) absolute zero C) nonsense

3) Temperature 185.2 ^oC is

A) –85.2 K B) 458.35 K C) 358.35 K

4) Temperature 0 K is

A) nonsense B) –273.15^oC C) 273.150^oC

5) A pupil said “The temperature of the water increased by 20^oK.” In reality it increased by

A) 20^oC B) 293.15^oC C) 253.15^oC

6) Temperature –1273.15^oC is

A) the freezing temperature of hydrogen B) nonsense C) 73.15 K

7) Temperature 290 K is

A) the temperature of a healthy person B) 290^oC C) 16.85^oC

8) Temperature 373.15 K is

A) boiling temperature of water B) nonsense C ) 0^oC

Solution:

1C, 2B, 3B, 4B, 5A, 6B, 7C, 8A

4.A steel rod has heat capacity C = 1.5·10³ J·K^-1. How will its temperature change if

a) it absorbs heat Q₁= 25·10³ J
b) it gives off heat Q₂ = 0.45·10⁶ J

Solution:

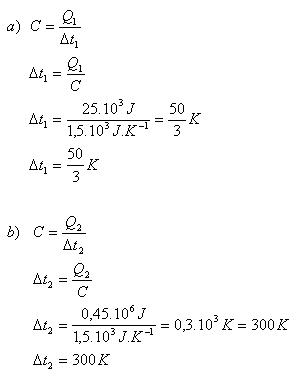
a) the temperature increases by 50/3 K
b) the temperature decreases by 300 K.

5.Calculate how long it takes for water to heat from 15^oC to the boiling temperature when heated by an immersion heater, if the volume of water is 150 cm³. The heater power is 500 W and its efficiency is 95%. c(H₂O) = 4180 J·kg^-1·K^-1.

Solution:

Analysis:

Δt = 100^oC – 15^oC = 85^oC, V = 150·10^-6 m³, P_in = 500 W, η = 0.95

c(H₂O) = 4180 J·kg^-1·K^-1, ρ(H₂O) = 10³ kg·m^-3

Amount of heat received by water:

Q = m \cdot c \cdot \Delta t = \rho \cdot V \cdot c \cdot \Delta t

Q = 10^3 \, \text{kg·m}^{-3} \cdot 150 \cdot 10^{-6} \, \text{m}^3 \cdot 4180 \, \text{J·kg}^{-1}\text{·K}^{-1} \cdot 85 \, K = 5.3295 \cdot 10^4 \, J

Q = 5.3295 \cdot 10^4 \, J

Time of heating water:

\eta = \frac{P}{P_p} \quad P = \eta \cdot P_p

P = \frac{Q}{\tau}

\tau = \frac{Q}{P} = \frac{Q}{\eta \cdot P_p}

\tau = \frac{5.3295 \cdot 10^4 \, J}{0.95 \cdot 500 \, W} = 112.2 \, \frac{J}{J/s} = 112.2 \, s = 1.87 \, min = 1 \, min \, 52 \, s

\tau = 1.87 \, min = 1 \, min \, 52 \, s

The water heats in just under 2 minutes.

6.To water with mass 2.5 kg and temperature 15^oC a steel cylinder of mass 0.9 kg at temperature 300^oC was inserted. What will be the final temperature of the water and the cylinder after reaching equilibrium?

Solution:

Analysis:

m₁ = 2.5 kg, m₂ = 0.9 kg, t₁ = 15^oC, t₂ = 300^oC
c₁(H₂O) = 4180 J·kg^-1·K^-1, c₂(Fe) = 452 J·kg^-1·K^-1
t = ?

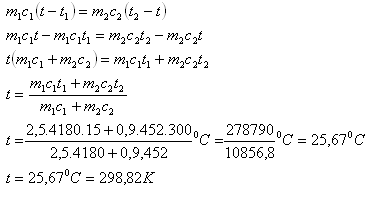
The final temperature of the water and cylinder will be t = 25.67^oC.

7.Five steel plates with a total mass of 7 kg were heated to 910^oC and immersed into oil at 10^oC. How many liters of oil must we use in the quenching bath so that the bath temperature stabilizes at 190^oC.

Solution:

Analysis:

Oil: t₁ = 10^oC, c₁ = 1760 J·kg^-1·K^-1, ρ₁ = 940 kg·m^-3, m₁ = ? V₁ = ?

Plates: t₂ = 910^oC, c₂ = 452 J·kg^-1·K^-1, m₂ = 7 kg,

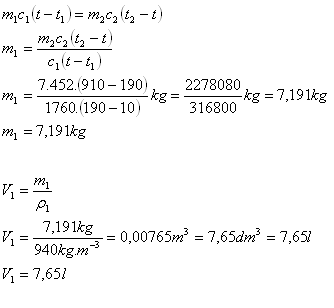
Final temperature t = 190^oC

8.There is 0.42 kg of water at 20^oC in a container. If we pour another 0.9 kg of water at 70^oC into the container, we find that the final temperature after reaching equilibrium is 50^oC. What is the heat capacity of the container?

Solution:

Analysis:

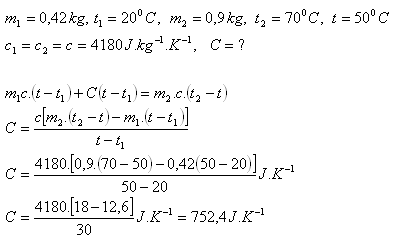
The heat capacity of the container is C = 752.4 J·K^-1

9.Into a container with C = 2 J·K^-1 was poured water of mass 0.4 kg and temperature 17^oC. A cylinder of unknown material with mass 0.124 kg and temperature 64^oC was placed into the container. The system temperature equilibrated at 19^oC. What material is the cylinder made of? Use tables!

Solution:

Analysis:

Water: m₁ = 0.4 kg, t₁ = 17^oC, c₁ = 4180 J·kg^-1·K^{-1 Cylinder: m₂ = 0.124 kg, t₂ = 64^oC, c₂ = ?

System temperature: t = 19^oC

Container: C = 2 J·K^-1}

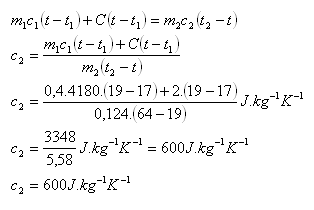
The cylinder is made of brass. (c(brass) = 590 J·kg^-1·K^-1)

10.When mixing 20 liters of water at 12^oC with 40 liters of water at 80^oC, 420 kJ of heat escaped into the air. Determine the final temperature of the water!

Solution:

Analysis:

m₁ = 20 kg, t₁ = 12^oC m₂ = 40 kg, t₂ = 80^oC, Q = 420·10³J,
c₁ = c₂ = c = 4180 J·kg^-1·K^-1, t = ?

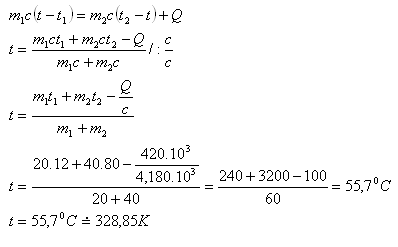
The final temperature of the water will be t = 55.7^oC

11.A body with a mass of 1 kg slides down an inclined plane 21 m long with a slope of 30⁰. The speed at which the body leaves the inclined plane is 4.1 m·s^-1. Determine the total change in internal energy of the body and the inclined plane.

Solution:

vnutorna-energia-11

The change in internal energy is 96.6 J.

12.Water with a mass of 1 kg was heated from a temperature of 0⁰C to 100⁰C and absorbed a certain amount of heat. Compare this heat with:

a.) the gravitational potential energy of this body at a height of 10 km
b.) the kinetic energy of this body at a speed of 100 m·s^-1.

Solution:

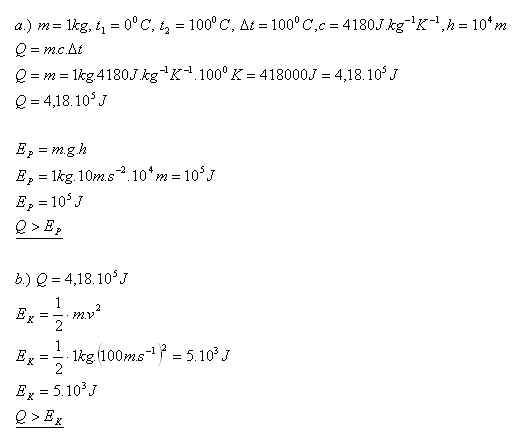
vnutorna-energia-12

13.How much heat is absorbed by oil (c = 1.7·10³ J·kg^-1·K^-1) with a volume of 2 l and density 910 kg·m^-3 when heated from 20⁰C to 65⁰C?

Solution:

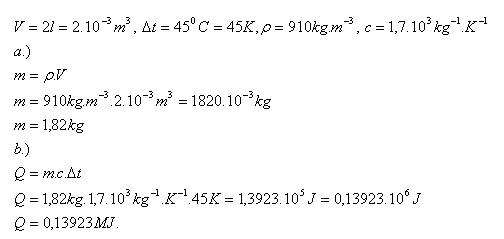
vnutorna-energia-13

The oil absorbs 0.13923 MJ of heat.

14.During turning (machining), both the cutting tool and the workpiece heat up, which is why they must be cooled by a coolant. The thermal power of the coolant is 50 kJ·min^-1. How many liters of coolant are needed for one hour of turning if its density is 980 kg·m^-3, initial temperature 20⁰C, final temperature 60⁰C and c = 3.9 kJ·kg^-1·K^-1?

Solution:

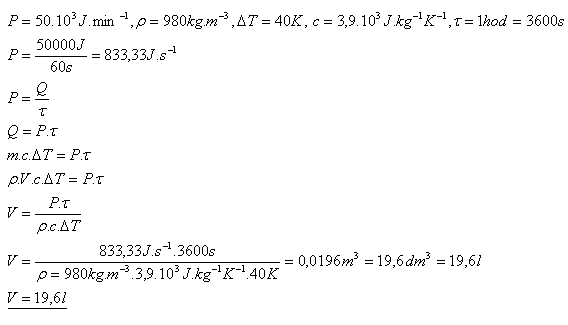
vnutorna-energia-15

For one hour of turning, 19.6 liters of coolant are needed.

15.A lead bullet flying at a speed of 100 m·s^-1 hit a stationary wooden board and lodged in it. Determine the temperature increase of the bullet if 50% of its kinetic energy is converted into its internal energy upon impact. (c(Pb) = 129 J·kg^-1·K^-1)

Solution:

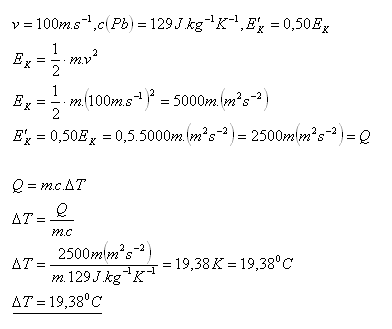
vnutorna-energia-16

The temperature increase of the bullet is 19.38⁰C.

16.An automobile has a four-cylinder engine with power P = 52 kW. Determine the efficiency of the engine if at a speed v = 120 km·h^-1 it consumes 15 liters of gasoline over a distance of 100 km.

H – calorific value of fuel = 46 MJ·kg^-1, ρ – fuel density = 700 kg·m^-3

Solution:

Analysis:

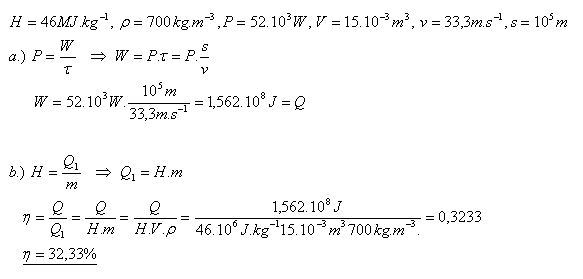
vnutorna-energia-17

The engine efficiency is 32.33%.

17.Determine the mass of gunpowder needed for a bullet with a mass of 50 g to reach a height of 2 km when fired vertically upward. Efficiency is 15%, calorific value 2.94 MJ·kg^-1. (Air resistance neglected)

Solution:

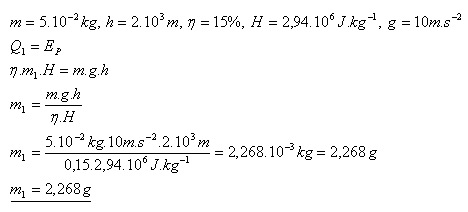
vnutorna-energia-18

The mass of gunpowder is 2.268 g.

18.In a vertical cylinder, a gas is enclosed by a movable piston with a mass of 1.5 kg. The gas absorbed 13 J of heat from the surroundings and simultaneously lifted the piston by 20 cm. How did its internal energy change?

Solution:

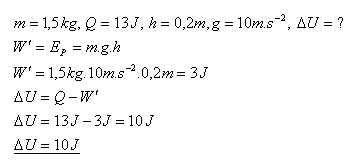
vnutorna-energia-19

The internal energy of the gas increases by 10 J.

19.In an iron container (cFe = 452 J·kg^-1·K^-1) with a mass of 0.1 kg there is water (cH₂O = 4180 J·kg^-1·K^-1) with a mass of 0.5 kg and temperature 15⁰C. An aluminum (cAl = 896 J·kg^-1·K^-1) and a lead (cPb = 129 J·kg^-1·K^-1) body with a total mass of 0.15 kg and temperature 100⁰C were placed into the container. After reaching equilibrium, the water temperature increased to 17⁰C. Determine the mass of the aluminum body (x) and the mass of the lead body (y).

Solution:

Calorimeter: C = c·m = 452·0.1 = 45.2 J

Heat absorbed by water and calorimeter:
Q = 0.5·4180·(17–15) + 45.2·(17–15) = 4270.4

Heat released by the aluminum body:
Q1 = x·896·(100–17) = 74368x

Heat released by the lead body:
Q2 = y·129·(100–17) = 10707y

vnutorna-energia-20

The aluminum body has a mass of 42 g, the lead body 108 g.

Physics

Internal energy

Adblock detected