Quantum optics
1. Čo je to fotón?
Riešenie:

2. Vypočítajte energiu fotónu, ktorý prislúcha krajným hodnotám viditeľného svetla. Fialová má vlnovú dĺžku λF=390 nm, červená fČ=790 nm. Vyjadrite v jouloch aj v eV. 1eV=1,602.10-19J.
Riešenie:
Rozbor:
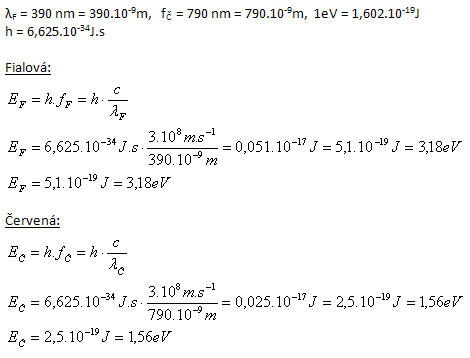
Fotón fialového svetla má energiu 3,18 eV, červeného 1,56 eV
3. Porovnajte energiu fotónu žltého monofrekvenčného svetla (λ = 500.10-9m) so strednou kinetickou energiou molekuly ideálneho plynu pri jej neusporiadanom pohybe pri teplote 00C.
Riešenie:
Rozbor:
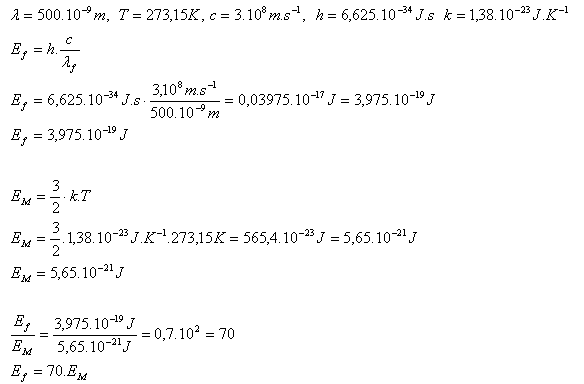
Energia fotónu žltého svetla je 70 krát väčšia ako energia molekuly ideálneho plynu pri teplote 00C.
4.
Ľudské oko môže vnímať svetlo, ak výkon svetelného žiarenia dopadajúceho na oko je minimálne P=2.10-17W. Určite koľko fotónov s vlnovou dĺžkou λ = 500.10-9m dopadne pri tom za 1 sekundu do oka.
Riešenie:
Rozbor:
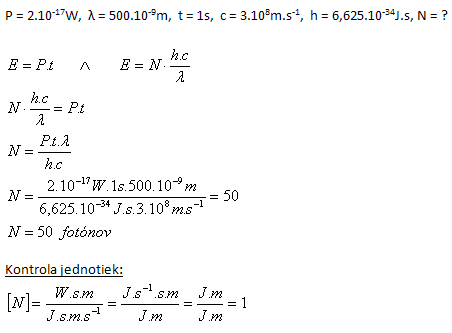
Za jednu sekundu dopadne do oka 50 fotónov.
5.
Aká je hraničná frekvencia elektromagnetického žiarenia, ktorým treba ožiariť povrch niklu, aby nastal vonkajší fotoelektrický jav. Výstupná práca elektrónov z niklu je 5 eV.
Riešenie:
Rozbor:
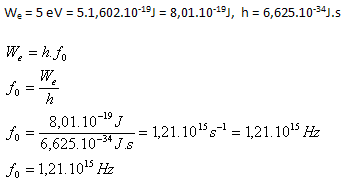
Hraničná frekvencia elektromagnetického žiarenia pre nikel je f0 = 1,21.1015Hz. Je to ultrafialové žiarenie.
6.
Zistite, či môže nastať fotoemisia pri dopade svetla s vlnovou dĺžkou λ = 390.10-9m na zinok.
Výstupná práca pre zinok je We = 4eV, λ = 390nm, We = 4eV = 4.1,602.10-19J = 6,408.10-19J, λ0 = ?
Riešenie:
Rozbor:
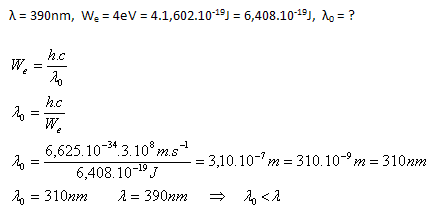
Fotoelektický jav nenastane lebo λ0 < λ .
7.
Akou rýchlosťou opúšťajú elektróny platinovú doštičku (f0 = 12,8.1014Hz), ak na ňu dopadá ultrafialové svetlo vlnovej dĺžky λ = 150nm. (me = 9,1.10-31kg)
Riešenie:
Rozbor:
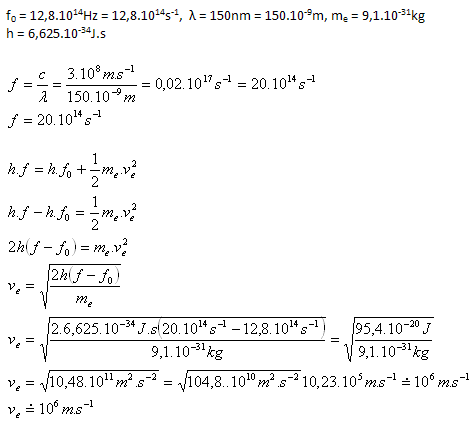
Elektróny opúšťajú platinovú doštičku rýchlosťou asi 106m.s-1.
8.
Dĺžka de Broglieho vlny urýchleného elektrónu je λ = 3,87.10-11m. Elektrón bol urýchlený z pokoja v elektrickom poli napätím U. Vypočítajte:
- a) rýchlosť elektrónu
- b) urýchľovacie napätie
Riešenie:
Rozbor:
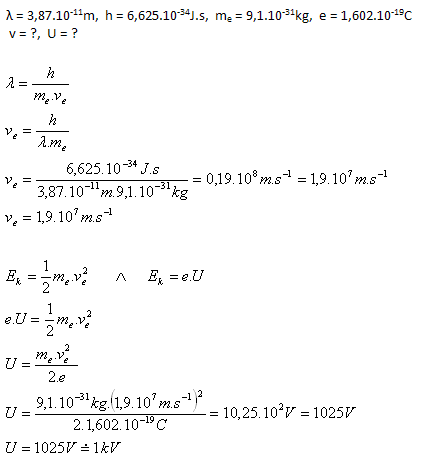
- Elektrón sa pohybuje rýchlosťou 1,9.107m.s-1
- Urýchľovacie napätie je 1kV
9.
Fotón ultrafialového žiarenia má vlnovú dĺžku λ = 100nm. Vypočítajte
- a) koľko fotónov má energiu 1J
- b) koľko fotónov má hmotnosť 1 mikrogram
Riešenie:
Rozbor:
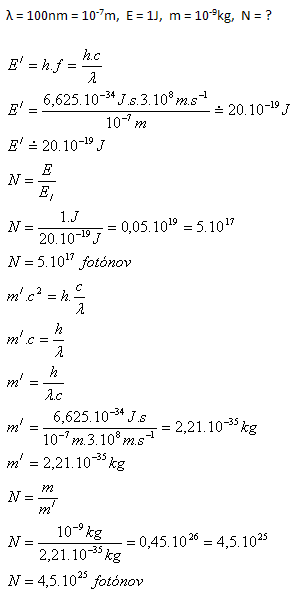
- Energiu 1J má 5.1017 fotónov
- Hmotnosť 1μg má 4,5.1025 fotónov.
10.
Pri Comptonovom pokuse má dopadajúci fotón frekvenciu f1=1,5.1020Hz, fotón po zrážke frekvenciu f2=1,1.1020Hz.
- a) Určite energiu, ktorú získal elektrón, ktorý bol v interakcii s fotónom. Vyjadrite v jednotkách eV
- b) Určite zmenu vlnovej dĺžky fotónu.
Riešenie:
Rozbor:

- Elektrón získa energiu 1,65 eV
- Fotón zmení vlnovú dĺžku o 0,727.10-12m
11.
Pri Franckovom – Hertzovom experimente autori zistili, že pokles prúdu nastáva pri napätí v elektrickom poli urýchľujúcom elektróny rovnajúcom sa U = 4,9V a že ortuťové pary vyžarujú žiarenie s vlnovou dĺžkou λ = 253,2nm. Vypočítajte hodnotu Planckovej konštanty h
Riešenie:
Rozbor:
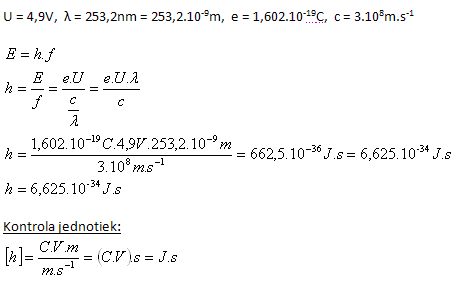
Plancková konštanta je h = 6,625.10–34J.s.
12. Pri Comptonovom jave rozptýlenia fotónov na elektróne, nastane zmena vlnovej dĺžky fotónu Δλ=4.85.10–12m. O aký uhol υ sa fotón odchýli od pôvodného smeru?
Riešenie:
Rozbor:
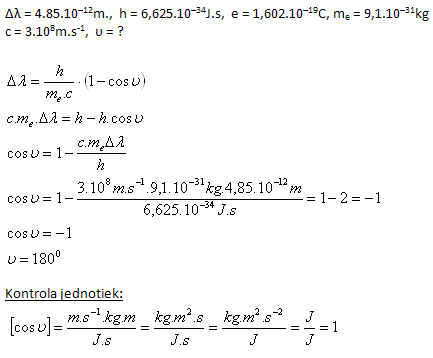
Uhol rozptylu je υ = 1800. Ide o takzvaný „rozptyl dozadu“.