Redox equations
Redox equations are chemical equations of redox reactions. In redox reactions, the oxidation numbers of atoms change, therefore knowledge of chemical nomenclature and the rules for determining oxidation numbers is an essential prerequisite for successfully solving redox equations.
Reduction is the process in which an atom lowers its oxidation number. Oxidation is the process in which an atom increases its oxidation number. The change in oxidation number occurs through the actual or formal transfer of electrons (oxidation) or the acceptance of electrons (reduction; since electrons have a negative electrical charge, their acceptance lowers the oxidation number).
Reducing agent is a reactant that causes the reduction of another reactant (at least one atom of the reducing agent increases its oxidation number). Oxidizing agent is a reactant that causes the oxidation of another reactant (at least one atom of the oxidizing agent decreases its oxidation number).
Half-equation expresses only oxidation or only reduction; in electrochemistry it is also called the electrode equation.
When solving redox equations, we follow general rules for calculating stoichiometric coefficients using the following procedure:
- Determine the oxidation numbers of all atoms in the equation.
- Write the half-equation for oxidation and the half-equation for reduction.
- Adjust the oxidation and reduction half-equations mathematically so that the electron balance rule is followed.
- Add and adjust both half-equations to obtain the simplified redox equation (SRR).
- Reflect the obtained atom counts in the chemical equation using stoichiometric coefficients.
- Based on the atom balance rule, assign stoichiometric coefficients to substances containing atoms that did not change their oxidation number.
- If it is an ionic redox equation, use the charge balance rule to determine stoichiometric coefficients.
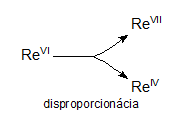
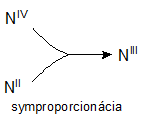
Simple disproportionation and comproportionation redox reactions are such chemical reactions in which the oxidation number of atoms of only one element changes; otherwise, they do not differ from other redox reactions.
Redox equations in which reactants contain atoms of a given element with one oxidation number and products contain atoms of the same element with different oxidation numbers are called disproportionation equations. For example:
3ReVIF6 + 10H2O → 2HReVIIO4 + ReIVO2 + 18HF
Redox equations in which reactants contain atoms of a given element with different oxidation numbers and products contain atoms of the same element with only one oxidation number are called comproportionation equations. For example:
NIVO2 + NIIO + 2NaOH → 2NaNIIIO2 + H2O
1. Balance the redox equation:
Solution:
The first step is to determine the oxidation states of the atoms in each compound:
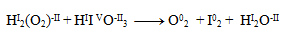
Thus, only iodine and oxygen change their oxidation numbers. We write half-reactions for them, i.e. reactions involving only the given oxidizing/reducing element and electrons.
Oxidation:
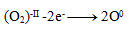
Reduction:
2IIV +10e- -------> 2I0
Next, we multiply the equations so that the number of electrons balances:
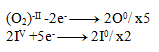
And then we add the equations:
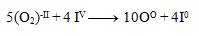
We substitute the obtained coefficients into the original equation and calculate the number of remaining atoms to comply with the law of conservation of atoms of the same element. The resulting equation has the form:
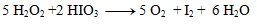
2.Complete the stoichiometric coefficients in the redox equation:
Solution:
First, it is necessary to determine the oxidation numbers of the atoms of all reactants and products:
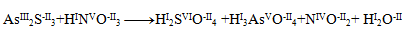
We can notice that only arsenic, sulfur and nitrogen change their oxidation numbers. For these elements we write half-reactions, in which we also indicate the number of exchanged electrons.
Oxidation equations:
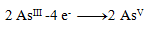
(one arsenic requires 2 electrons)
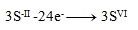
(one sulfur requires 8 electrons)
Reduction equation:
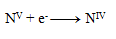
The next step is to adjust the number of exchanged electrons so that the same number is exchanged in oxidations and reductions—thus, in all three half-reactions, 28 electrons will be exchanged. 24+4=28 electrons in oxidation, so the same must occur in reduction, therefore:
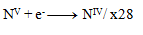
and thus
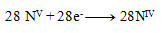
The stoichiometric coefficients from the half-reactions are added into the equation and the other elements are calculated. The resulting equation has the form:
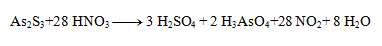
3. Balance the following redox equations:
Solution:
- a) 3,4,3,4,2
- b) 5,2,5,1,6
- c) 2,11,11,6,2,11,8
- d) 1,1,2,1,2,2
- e) 4,11,2,8
- f) 3,10,2,1,18
- g) 5,1,6,3,3
- h) 1,1,1,2
- i) 3,6,1,5,3
4.Determine the stoichiometric coefficients in the following chemical equation:
Cr + H2SO4 → Cr2(SO4)3 + H2
Solution:
We calculate the oxidation numbers of all atoms. We find that the oxidation numbers of chromium and hydrogen change:
Cr0 + HI2SVIO–II4 → CrIII2(SVIO–II4)3 + H02
We write the half-equations of oxidation and reduction:
Cr0 – 3e– → CrIII (oxidation)
HI + 1e– → H0 (reduction)
Since the number of accepted and released electrons must be equal, we multiply the second half-equation by three:
Cr0 – 3e– → CrIII
3HI + 3e– → 3H0
Now the number of electrons is balanced. We add the half-equations:
Cr0 – 3e– + 3HI + 3e– → CrIII + 3H0
After simplification:
Cr0 + 3HI → CrIII + 3H0
This represents the simplified redox equation (SRR). To obtain stoichiometric coefficients, we adjust further:
2Cr + 3H2SO4 → Cr2(SO4)3 + 3H2
5. Determine the stoichiometric coefficients in the following chemical equation:
Ca3(PO4)2 + SiO2 + C → P4 + CaSiO3 + CO
Solution:
We calculate the oxidation numbers of all atoms. We find that the oxidation numbers of phosphorus and carbon atoms change:
CaII3(PVO–II4)2 + SiIVO–II2 + C0 → P04 + CaIISiIVO–II3 + CIIO–II
We write the partial oxidation and reduction equations:
C0 – 2e– → CII (oxidation)
PV + 5e– → P0 (reduction)
Since the number of accepted and released electrons must be equal, we multiply the first partial equation by five and the second partial equation by two:
5C0 – 10e– → 5CII
2PV + 10e– → 2P0
The number of accepted and released electrons is the same. From this point we can only apply the same mathematical operations to both partial equations simultaneously so that the number of accepted and released electrons remains equal. Therefore, we add both partial equations and obtain the redox equation:
5C0 – 10e– + 2PV + 10e– → 5CII + 2P0
after simplification:
5C0 + 2PV → 5CII + 2P0
The numerical values we obtained are not stoichiometric coefficients, but represent the numbers of atoms that must be present on the left and right side of the equation. On the right side, according to the redox equation, we should have two phosphorus atoms with oxidation number 0. However, these occur as tetratomic molecules, so the stoichiometric coefficient would have a fractional value. Therefore, we multiply the redox equation by 2:
10C0 + 4PV → 10CII + 4P0
On the left side of the equation we need to have four phosphorus atoms, so we place coefficient 2 before Ca3(PO4)2. On the right side we also need to have four phosphorus atoms, which are already ensured by the subscript 4 in P4, so this substance has coefficient 1:
2Ca3(PO4)2 + SiO2 + C → P4 + CaSiO3 + CO
On both sides of the equation we must have ten carbon atoms. Therefore, we place coefficient 10 in front of C and likewise in front of CO:
2Ca3(PO4)2 + SiO2 + 10C → P4 + CaSiO3 + 10CO
We still need coefficients before SiO2 and CaSiO3. On the left side we have 6 calcium atoms, so we put coefficient 6 before CaSiO3. This means that we must also have 6 silicon atoms on the left, so we put coefficient 6 before SiO2.
2Ca3(PO4)2 + 6SiO2 + 10C → P4 + 6CaSiO3 + 10CO
In this way, all substances in the chemical equation received their stoichiometric coefficients. We verify the solution by counting the oxygen atoms on both sides of the equation (28 = 28). Since the obtained stoichiometric coefficients (2, 6, 10 = 1, 6, 10) do not have any common divisor other than 1, the balancing of the chemical equation is complete.
6.Find the stoichiometric coefficients in the following chemical equation:
MnO4– + Fe2+ + H3O+ → Mn2+ + Fe3+ + H2O
Solution:
We calculate the oxidation numbers of all atoms. We find that the oxidation numbers of manganese and iron atoms change:
(MnVIIO–II4)– + Fe2+ + (HI3O–II)+ → Mn2+ + Fe3+ + HI2O–II
We write the half-reactions of oxidation and reduction (the oxidation number of monatomic ions is identical to their charge number):
Fe2+ – e– → Fe3+ (oxidation)
MnVII + 5e– → MnII (reduction)
Since the number of accepted and donated electrons must be equal, we multiply the first half-reaction by five and add both half-reactions:
5Fe2+ – 5e– → 5Fe3+
MnVII + 5e– → MnII
5Fe2+ – 5e– + MnVII + 5e– → 5Fe3+ + MnII
After adjustment, we get the redox reaction:
5Fe2+ + MnVII → 5Fe3+ + MnII
The numerical values we obtained express the number of atoms that must be on both the left and right sides of the chemical equation. Since there must be five iron atoms on both sides of the equation, we place the coefficient 5 in front of the Fe2+ and Fe3+ ions.
MnO4– + 5Fe2+ + H3O+ → Mn2+ + 5Fe3+ + H2O
The coefficient of MnO4– and Mn2+ must be 1, which is already satisfied. Two substances remain in the equation without coefficients: the reactant – the oxonium cation, and the product – water. Since this is an ionic equation, we use the rule of balancing charge numbers. On the right side of the equation, all ions already have coefficients; the sum of charge numbers on the right side of the equation is 1·2 + 5·3 + 1·0 = 17. On the left side of the equation we must also have a sum of charge numbers equal to 17, but so far (besides H3O+) we have: 1·(–1) + 5·2 = 9. We need to increase this sum by 8, therefore the coefficient before H3O+ will be 8:
MnO4– + 5Fe2+ + 8H3O+ → Mn2+ + 5Fe3+ + H2O
(To calculate the stoichiometric coefficient for H3O+, we could also use the rule of charge balance in the form of an equation, where the coefficient for H2O is denoted as y and the coefficient for H3O+ as x. It holds: 1·(–1) + 5·2 + x·1 = 1·2 + 5·3 + y·0. From the equation, it follows that x = 8.)
On the left side of the equation, we have 8·3 = 24 hydrogen atoms, so on the right side we must place coefficient 12 before H2O:
MnO4– + 5Fe2+ + 8H3O+ → Mn2+ + 5Fe3+ + 12H2O
By this process, we obtained stoichiometric coefficients for all substances in the chemical equation. We verify the solution by counting the oxygen atoms on both sides of the equation (12 = 12). Since the obtained stoichiometric coefficients (1, 5, 8 = 1, 5, 12) have no common divisor other than 1, the balancing of the chemical equation is complete.
7. Find the stoichiometric coefficients in the following chemical equation:
Cu + HNO3 → Cu(NO3)2 + NO2 + H2O
Solution:
We calculate the oxidation numbers of all atoms. We find that the oxidation numbers of copper and nitrogen change:
Cu0 + HINVO–II3 → CuII(NVO–II3)2 + NIVO–II2 + HI2O–II
We write the partial (half) reactions for oxidation and reduction:
Cu0 – 2e– → CuII (oxidation)
NV + e– → NIV (reduction)
Since the number of electrons gained and lost must be equal, we multiply the second half-reaction by two and add both half-reactions:
Cu0 – 2e– → CuII
2NV + 2e– → 2NIV
Cu0 – 2e– + 2NV + 2e– → CuII +2NIV
and after simplification we obtain SRR:
Cu0 + 2NV → CuII +2NIV
The numerical values we obtained are not the stoichiometric coefficients but express the numbers of atoms that must appear on the left and right sides of the chemical equation. On both sides of the equation we must have one copper atom, so the coefficient before Cu and Cu(NO3)2 will be 1. On the right-hand side we must have two nitrogen atoms with oxidation number IV, therefore we place coefficient 2 before NO2:
Cu + HNO3 → Cu(NO3)2 + 2NO2 + H2O
On the left-hand side we must have two nitrogen atoms with oxidation number V, but we cannot put coefficient 2 before HNO3 because not all nitrogen atoms participate in the redox process. On the right-hand side there are also nitrogen atoms with unchanged oxidation number – in Cu(NO3)2. Therefore the stoichiometric coefficient before HNO3 must be larger than the one obtained from the partial reactions. This coefficient must account both for the redox and the non-redox portions. We already have coefficient 1 before Cu(NO3)2, which contains two nitrogen atoms with oxidation number V. Hence we put coefficient 4 before HNO3: two nitrogen atoms took part in the redox process and two did not change their oxidation number:
Cu + 4HNO3 → Cu(NO3)2 + 2NO2 + H2O
The last substance without a stoichiometric coefficient is water. On the left-hand side we have 4 hydrogen atoms, therefore we place coefficient 2 before H2O:
Cu + 4HNO3 → Cu(NO3)2 + 2NO2 + 2H2O
In this way we obtained the stoichiometric coefficients for all substances in the chemical equation. We verify the solution by counting oxygen atoms on both sides of the equation (12 = 12). Since the obtained stoichiometric coefficients (1, 4 = 1, 2, 2) have no common divisor other than 1, the balancing of the chemical equation is complete.
8. Find the stoichiometric coefficients in the following chemical equation:
KMnO4 + HBr → Br2 + MnBr2 + KBr + H2O
Solution:
|
We calculate the oxidation numbers of all atoms. We find that the oxidation numbers of manganese and bromine change:
Br02 + MnIIBr–I 2 + KIBr–I + H2O–II
We write the partial (half) reactions for oxidation and reduction:
Br0 (oxidation)
MnII (reduction)
Since the number of electrons gained and lost must be equal, we multiply the first half-reaction by five and add the partial reactions:
5Br0
MnII
5Br–I – 5e– + MnVII + 5e–= 5Br0 + MnII
and after simplification we obtain SRR:
5Br0 + MnII
On the right-hand side of the equation we must have, according to SRR, five bromine atoms with oxidation number 0. However, bromine exists as diatomic molecules, so the stoichiometric coefficient would be fractional. Therefore we multiply SRR by 2:
10Br–I + 2MnVII → 10Br0 + 2MnII
The numerical values we obtained are not the stoichiometric coefficients but express the numbers of atoms that must appear on the left and right sides of the chemical equation. On both sides we must have two manganese atoms, so the coefficient before KMnO4 and MnBr2 will be 2:
2KMnO4 + HBr → Br2 + 2MnBr2 + KBr + H2O
At the same time, on the left-hand side we must have ten bromine atoms with oxidation number –I, but we cannot put coefficient 10 before HBr because on the right-hand side bromine also appears with unchanged oxidation number –I. Thus the coefficient before HBr must be larger than 10. On the right-hand side we must have 10 bromine atoms with oxidation number 0, therefore we put coefficient 5 before Br2:
2KMnO4 + HBr → 5Br2 + 2MnBr2 + KBr + H2O
On the left-hand side we have two potassium atoms, therefore we place coefficient 2 before KBr:
2KMnO4 + HBr → 5Br2 + 2MnBr2 + 2KBr + H2O
Since we now have coefficients before all bromine-containing substances on the right-hand side, we find that there are 16 bromine atoms on the right, therefore we put coefficient 16 before HBr:
2KMnO4 + 16HBr → 5Br2 + 2MnBr2 + 2KBr + H2O
The coefficient 16 before HBr also means that 10 bromine atoms participated in the redox reaction and the remaining six remained unchanged. On the left-hand side there are also 16 hydrogen atoms, therefore we put coefficient 8 before H2O on the right:
→ 5Br2 + 2MnBr2 + 2KBr + 8H2O
In this way we obtained the stoichiometric coefficients for all substances in the chemical equation. We verify the solution by counting oxygen atoms on both sides of the equation (8 = 8). Since the obtained stoichiometric coefficients (2, 16 = 5, 2, 2, 8) have no common divisor other than 1, the balancing of the chemical equation is complete.
|
9. Find the stoichiometric coefficients in the following chemical equation:
ReF6 + H2O → HReO4 + ReO2 + HF
Solution:
|
We calculate the oxidation numbers of all atoms. We find that only the oxidation number of the rhenium atom changes:
ReVIF–I6 + HI2O–II → HIReVIIO–II4 + ReIVO–II2 + HIF–I
This is a disproportionation equation. We write the partial (half) reactions for oxidation and reduction:
ReVII (oxidation)
→ ReIV (reduction)
Since the number of electrons gained and lost must be equal, we multiply the first half-reaction by two and add the partial reactions:
2ReVI – 2e– → 2ReVII
ReVI + 2e– → ReIV
2ReVI – 2e– + ReVI + 2e– = 2ReVII + ReIV
After simplification we obtain SRR:
2ReVII + ReIV
From SRR it follows that on the left-hand side we must have three rhenium atoms with oxidation number VI and on the right-hand side two rhenium atoms with oxidation number VII and one atom with oxidation number IV. We add stoichiometric coefficients to the redox equation:
3ReF6 + H2O → 2HReO4 + ReO2 + HF
On the left-hand side we have 18 fluorine atoms, therefore we put coefficient 18 before HF:
3ReF6 + H2O → 2HReO4 + ReO2 + 18HF
The only substance without a stoichiometric coefficient is water. On the right-hand side we have 2 + 18 = 20 hydrogen atoms, therefore we put coefficient 10 before H2O:
2HReO4 + ReO2 + 18HF
|
In this way we obtained the stoichiometric coefficients for all substances in the chemical equation. We verify the solution by counting oxygen atoms on both sides of the equation (10 = 10). Since the obtained stoichiometric coefficients (3, 10 = 2, 1, 18) have no common divisor other than 1, the balancing of the chemical equation is complete.
10.Determine the stoichiometric coefficients in the following chemical equation:
MnO42– + H3O+ → MnO4– + MnO2 + H2O
Solution:
|
Calculate the oxidation numbers of all atoms. We find that only the oxidation number of the manganese atom changes:
(MnVIO–II4)2– + (HI3O–II)+ → (MnVIIO–II4)– + MnIVO–II2 + HI2O–II
This is a disproportionation equation. We write the partial oxidation and reduction equations:
MnVI – 1e– → MnVII (oxidation)
MnVI + 2e– → MnIV (reduction)
Since the number of electrons accepted and released must be the same, we multiply the first partial equation by two and add the partial equations:
2MnVI – 2e– → 2MnVII
<>MnVI + 2e– → MnIV
2MnVI – 2e– + MnVI + 2e– → 2MnVII + MnIV
and after adjustment we obtain the net ionic result:
→ 2MnVII + MnIV
From this it follows that on the left side of the equation we must have three manganese atoms with oxidation number VI, and on the right side two manganese atoms with oxidation number VII and one atom with oxidation number IV. We add stoichiometric coefficients to the redox equation:
3MnO42– + H3O+ → 2MnO4– + MnO2 + H2O
Two species in the equation remain without coefficients: the reactant—oxonium cation—and the product—water. Since this is an ionic equation, we use charge balance. On the right side only one ion has a coefficient, so we can compute the sum of charges: 2 · (–1) + 1 · 0 + 1 · 0 = –2. On the left side we must also have a total charge of –2, but we currently have (besides H3O+): 3 · (–2) = –6. We need to increase this sum by 4, therefore the coefficient in front of H3O+ will be 4:
3MnO42– + 4H3O+ → 2MnO4– + MnO2 + H2O
On the left we have 12 hydrogen atoms, so we put the coefficient 6 in front of H2O:
3MnO42– + 4H3O+ → 2MnO4– + MnO2 + 6H2O
|
By this procedure, all substances in the chemical equation obtain stoichiometric coefficients. We verify the solution by counting the oxygen atoms on both sides of the equation (16 = 16). Since the obtained stoichiometric coefficients (3, 4 = 2, 1, 6) have no common divisor other than 1, the balancing of the chemical equation is complete.
11. Determine the stoichiometric coefficients in the following chemical equation:
NO2 + NO + NaOH → NaNO2 + H2O
Solution:
|
Calculate the oxidation numbers of all atoms. We find that only the oxidation number of the nitrogen atom changes; we underline its symbols:
NIVO–II2 + NIIO–II + NaIO–IIHI → NaINIIIO–II2 + HI2O–II
This is a comproportionation equation. We write the partial oxidation and reduction equations:
NII – 1e– → NIII (oxidation)
NIV + 1e– → NIII (reduction)
Since the number of electrons accepted and released is already the same, we add the partial equations:
NIII
→ NIII
NII – 1e– + NIV + 1e– →NIII + NIII
and after adjustment we obtain the net ionic result:
NII + NIV → 2NIII
From this it follows that on the right side of the equation we must have two nitrogen atoms with oxidation number III, and on the left one nitrogen atom with oxidation number II and one with IV. We add stoichiometric coefficients to the redox equation:
NO2 + NO + NaOH → 2NaNO2 + H2O
On the right side there are two sodium atoms, so we place the coefficient 2 in front of NaOH:
NO2 + NO + 2NaOH → 2NaNO2 + H2O
The only substance without a stoichiometric coefficient is water. On the left side we have 2 hydrogen atoms, so the coefficient in front of H2O must be 1:
NO2 + NO + 2NaOH → 2NaNO2 + H2O
|
By this procedure, all substances in the chemical equation obtain stoichiometric coefficients. We verify the solution by counting the oxygen atoms on both sides of the equation (5 = 5). Since the obtained stoichiometric coefficients (1, 1, 2 = 2, 1) have no common divisor other than 1, the balancing of the chemical equation is complete.
12. Find the stoichiometric coefficients in the following chemical equation:
I– + IO3– + H3O+ → I2 + H2O
Solution:
|
We calculate the oxidation numbers of all atoms. We find that only the oxidation numbers of the iodine atoms change; we underline their symbols:
→ I02 + HI2O–II
This is a symproportionation (comproportionation) equation. We write the half-reactions for oxidation and reduction:
→ I0 (oxidation)
IV + 5e– → I0 (reduction)
Because the number of electrons accepted and donated must be equal, we multiply the first half-reaction by five and add the half-reactions:
5I–I – 5e– → 5I0
IV + 5e– → I0
5I–I – 5e– + IV + 5e– → 5I0 + I0
After simplification we obtain the net atom-reconciliation relation (ARR):
5I–I + IV → 6I0
The numerical values we obtained are not the stoichiometric coefficients but express the numbers of atoms that must appear on the left and right sides of the chemical equation. From the ARR it follows that the left side must contain five iodine atoms with oxidation number –I, so we place coefficient 5 before I–. Also, there must be one iodine atom with oxidation number V on the left, so the coefficient before IO3– is 1. On the right side there must be six iodine atoms with oxidation number 0, therefore we put coefficient 3 before I2:
5I– + IO3– + H3O+ → 3I2 + H2O
Two species in the equation still lack coefficients: the reactant oxonium cation and the product water. Since this is an ionic equation, we use the rule of charge balance. On the right side there are no ions, so the sum of charges on the right is zero. The same total charge must be on the left. So far (excluding H3O+) we have 5·(–1) + 1·(–1) = –6. We need to increase this sum by +6, therefore the coefficient before H3O+ will be 6:
5I– + IO3– + 6H3O+ → 3I2 + H2O
There are 18 hydrogen atoms on the left, so we put coefficient 9 before H2O:
5I– + IO3– + 6H3O+ → 3I2 + 9H2O
With this procedure we obtained the stoichiometric coefficients for all species in the chemical equation. We verify the solution by counting oxygen atoms on both sides (9 = 9). Since the obtained coefficients (5, 1, 6 = 3, 9) have no common divisor other than 1, balancing the chemical equation is complete.
|
13. Find the stoichiometric coefficients in the following chemical equation (More challenging problem for a chemistry olympiad):
Solution:
|
We calculate the oxidation numbers of all atoms. We find that the oxidation numbers of all atoms change: iron, sulfur, and oxygen:
FeIIS–I2 + O02 → FeIII2O–II3 + SIVO–II2
We write the half-reactions for oxidation and reduction:
FeII – 1e– → FeIII (oxidation)
S–I – 5e– → SIV (oxidation)
O0 + 2e– → O–II (reduction)
Since iron and sulfur occur together in the same compound on the left, their mutual ratio indicated by stoichiometric indices must be preserved. Therefore we multiply the first half-reaction by one, the second half-reaction by two and add them:
FeII – 1e– → FeIII
2S–I – 10e– → 2SIV
FeII – 1e– + 2S–I – 10e– → FeIII + 2SIV
After adjustment we obtain the combined half-reaction:
FeII + 2S–I – 11e– → FeIII + 2SIV
We will now adjust this combined half-reaction together with the half-reaction for oxygen:
FeII + 2S–I – 11e– → FeIII + 2SIV
O0 + 2e– →O–II
Because the number of electrons accepted and donated must be equal, we multiply the first combined half-reaction by 2 and the oxygen half-reaction by 11 and add them:
2FeII + 4S–I – 22e– → 2FeIII + 4SIV
11O0 + 22e– → 11O–II
2FeII + 4S–I – 22e– + 11O0 + 22e– → 2FeIII + 4SIV + 11O–II
After simplification we obtain the ARR:
2FeII + 4S–I + 11O0 → 2FeIII + 4SIV + 11O–II
The left side must contain eleven oxygen atoms with oxidation number 0. Since oxygen is present as diatomic molecules, the stoichiometric coefficient would be fractional. Therefore we multiply the ARR by 2:
4FeII + 8S–I + 22O0 → 4FeIII + 8SIV + 22O–II
The left side should contain 4 iron atoms and 8 sulfur atoms, so we put coefficient 4 before FeS2. We also need 22 oxygen atoms on the left, so we put coefficient 11 before O2:
4FeS2 + 11O2 → Fe2O3 + SO2
On the right side there must also be four iron atoms and eight sulfur atoms, therefore we put coefficient 2 before Fe2O3 and coefficient 8 before SO2:
4FeS2 + 11O2 → 2Fe2O3 + 8SO2
With this procedure we obtained the stoichiometric coefficients for all species in the chemical equation. We verify the solution by counting oxygen atoms on both sides (22 = 22). Since the coefficients (4, 11 = 2, 8) have no common divisor other than 1, balancing is complete.
|
14. Find the stoichiometric coefficients in the following chemical equation (More challenging problem for a chemistry olympiad):
Au + KCN + O2 + H2O → K[Au(CN)2] + KOH
Solution:
|
We calculate the oxidation numbers of all atoms. Since the cyanide anion essentially remains unchanged during the reaction (only coordinated), we do not need to determine oxidation numbers of carbon and nitrogen separately; it is sufficient to consider the charge of the whole CN– anion. We find that the oxidation numbers of gold and oxygen change.
Au0 + KICN– + O02 + HI2O–II → KI[AuI(CN–)2] + KIO–IIHI
We write the half-reactions for oxidation and reduction:
Au0 – 1e– → AuI (oxidation)
O0 + 2e– → O–II (reduction)
Because the number of electrons accepted and donated must be equal, we multiply the first half-reaction by two and add the half-reactions:
2Au0 – 2e– → 2AuI
O0 + 2e– → O–II
2Au0 – 2e– + O0 + 2e– → 2AuI + O–II
and after simplification we obtain the ARR:
2Au0 + O0 → 2AuI + O–II
The left side must contain two oxygen atoms in oxidation state 0, but oxygen is diatomic, so the stoichiometric coefficient would be fractional. Therefore we multiply the ARR by 2:
4Au0 + 2O0 → 4AuI + 2O–II
The numerical values obtained express numbers of atoms that must be on the left and right. Both sides must contain four gold atoms, so the coefficient before Au and before K[Au(CN)2] will be 4.
4Au + KCN + O2 + H2O → 4K[Au(CN)2] + KOH
Also, the left side must contain two oxygen atoms in oxidation state 0, which is already satisfied by coefficient 1 before O2. We cannot place coefficient 2 before KOH on the right because it contains not only the oxygen atoms participating in the redox reaction but also those coming from the water reactant. Since there are eight cyanide anions on the right, we place coefficient 8 before KCN:
4Au + 8KCN + O2 + H2O → 4K[Au(CN)2] + KOH
There are eight potassium atoms on the left; on the right four potassium atoms are bound in 4K[Au(CN)2], therefore we put coefficient 4 before KOH:
4Au + 8KCN + O2 + H2O → 4K[Au(CN)2] + 4KOH
The last species without a stoichiometric coefficient is water. Since there are four hydrogen atoms on the right, we put coefficient 2 before H2O:
4Au + 8KCN + O2 + 2H2O → 4K[Au(CN)2] + 4KOH
With this procedure we obtained stoichiometric coefficients for all species in the chemical equation. We verify the solution by counting oxygen atoms on both sides (4 = 4). Since the coefficients (4, 8, 1, 2 = 4, 4) have no common divisor other than 1, balancing is complete.
|