Malicious numbers

There is a question of whether it is possible to generate prime numbers according to a generally valid formula. The Swiss mathematician L. Euler (1707 – 1783) proposed the formula p = n² + n + 41.

n = 1,    p = 43 – prime

n = 2,    p = 47 – prime

n = 3,    p = 53 – prime

n = 40, p = 1681 – not a prime, because 1681 = 41 × 41

The French mathematician P. Fermat (1601 – 1665) studied the formula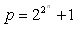

n = 1,    p = 2^₂1 + 1 = 5 – prime

n = 2,    p = 2^₂2 + 1 = 17 – prime

n = 3,    p = 2^₂3 + 1 = 257 – prime

n = 36, p = 2^₂36 + 1 is not a prime, because it is divisible by 2,748,779,069,441

 

Another approach to finding prime numbers was proposed by the French mathematician M. Mersenne (1588 – 1648). He suggested a formula for calculating “Mersenne primes”:

p = 2ⁿ – 1. For 2ⁿ – 1 to be prime, n itself must also be a prime.

n = 2, p = 2² – 1 = 3 – prime

n = 3, p = 2³ – 1 = 7 – prime

n = 5, p = 2⁵ – 1 = 31 – prime

n = 11, p = 2¹¹ – 1 = 2047 – not a prime, because 2047 = 23 × 89

Always at least one “mischievous number” ruined hopeful expectations. So far, 24 “Mersenne primes” are known for the exponents:

n = 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127, 521, 607, 1279, 2203, 2281, 3217, 4253, 4423, 9689, 9941, 11213, 19937.

Probably the largest known “Mersenne prime” is p = 2¹⁹⁹³⁷ – 1, calculated by a computer. It has more than 6000 digits. Prime “twins” are two prime numbers between which stands exactly one composite number:

 

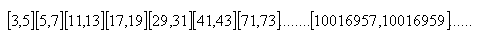
“Triplets” are only 3, 5, 7. “Quadruplets” do not exist.

 Literature: Opava, Z.: Mathematics Around Us, Prague, Albatros 1989.

---